
Оптимизация в среде MATLAB
..pdfОбращение к функции возможно по одному из приводимых ниже вариантов:
x = simulannealbnd(fun,x0)
x = simulannealbnd(fun,x0,lb,ub)
x = simulannealbnd(fun,x0,lb,ub,options) x = simulannealbnd(problem)
[x,fval] = simulannealbnd(...) [x,fval,exitflag] = simulannealbnd(...)
[x,fval,exitflag,output] = simulannealbnd(fun,...)
Смысл всех аргументов ясен из рассмотрения предыдущих функций оптимизации. Первый вариант применяется, если решается задача на безусловный экстремум. При наличии границ на переменные используется второй вариант. Если устанавливаются свои значения некоторых параметров, то обязателен третий вариант. На месте отсутствующих входных аргументов (кроме последнего) записывается [].
Содержание выходных аргументов exitflag и output специфично для данной функции. Exitflag сообщает причину завершения алгоритма через значения:
1 – среднее значение целевой функции по StallIterLimit итерациям меньше, чем TolFun,
5 – достигнут предел ObjectiveLimit,
0 – исчерпано максимальное число вычислений функции или итераций,
-1 – процесс остановлен функцией вывода или графики, -2 – не найдено допустимой точки, -5 – исчерпан лимит времени.
Структура output содержит информацию о задаче и выполнении алгоритма в следующих полях:
problemtype – тип задачи (без ограничений или с границами), iterations – число итераций,
funccount – число вычислений целевой функции, message – сообщение о причине останова, temperature – температура на момент остановки, totaltime – общее время работы решателя,
rngstate – состояние датчика случайных чисел перед началом работы алгоритма.
Рассмотрим примеры применения функции simulannealbnd.
91
Пример 13.
Методом Simulated Annealing найти минимум исследованной ранее в примерах 7 и 9 функции
f = 3(1– x1)2exp (– x12 – (x2 + 1)2) –10( x1/5 – x13 – x25 )exp (– x12 – x12 ) – –1/3exp (–(x1 + 1)2 – x22 )
при условиях
–3 xj 3, j = 1, 2.
Эта функция записана в m-файлах myfun(x) и myfun1(X,Y), последний из них предназначен для графического отображения функции. Для получения численного ответа достаточно обратиться к функции метода по одному из описанных выше вариантов. Однако мы составим программу нахождения минимума с именем runsa, используя в ней не только первый, но и второй файл целевой функции с тем, чтобы полнее и нагляднее представить результаты работы метода.
function history=runsa(x0)
history.x=x0;
history.fval=[];
options= saoptimset('PlotFcn',@outfun); history.t=[]; [x,fval,exitflag,output]=simulannealbnd(@myfun,x0,...
[-3 -3], [3 3],options) y=history.x(:,1);z=history.x(:,2); plot(y,z,'r.',x(1),x(2),'r*'); text(x0(1),x0(2)+0.12,'x0');
hold on; [X,Y]=meshgrid(-3:0.03:3);Z=myfun1(X,Y); contour(X,Y,Z,25,'blue');xlabel('x1');;ylabel('x2');
function stop = outfun(options,optimvalues,flag) stop = false;
switch flag case 'init'
hold on case 'iter'
%Concatenate current point, objective
%function and temperature history.fval = [history.fval;...
optimvalues.bestfval]; history.x = [history.x;...
92
optimvalues.bestx]; history.t=[history.t;...
optimvalues.temperature];
end
end
t1=[];for i=1:2:output.iterations; t1(i)=history.t(i);
end
figure;plot(t1);xlabel('N of iteration'); ylabel('t1');
end
Запустим программу из двух начальных точек: >> x0=[2 2.5]; history=runsa(x0)
Optimization terminated: change in best function value less than options.TolFun.
x =
0.2270 -1.6230 fval =
-6.5510 exitflag =
1
output =
Iterations: 1650 funccount: 1669 message: [1x80 char] rngstate: [1x1 struct]
problemtype: 'boundconstraints' temperature: [2x1 double] totaltime: 11.8281
history =
x: [1651x2 double] fval: [1650x1 double] t: [3300x1 double]
Решение получено за 1650 итераций, на что потребовалось 11,83 с. В результате найден глобальный минимум. На рис. 25 на фоне линий уровня целевой функции показаны лучшие точки, начиная с x0, а на рис. 26 – изменение температуры в измерении x1.
93
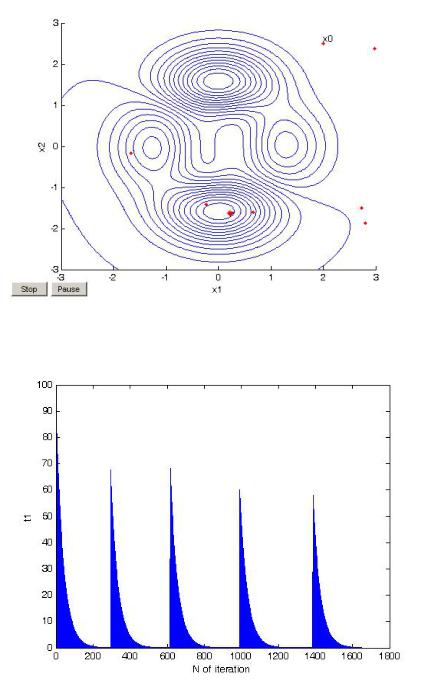
Рис. 25. Поиск минимума функции myfun из точки (2 2,5)
методом simulannealbnd
Рис. 26. График изменения температуры по x1 при поиске из точки (2 2,5)
94
Как видно, переотжиг происходил четыре раза через интервалы от 300 до 400 итераций. Узнаем температуру в финальной точке:
по x1 >> history.t(3299) ans =
0.2962 по x2 >> history.t(3300)
ans =
0.2882
Повторим поиск из новой точки: >> x0=[-1 1]; history=runsa(x0)
Optimization terminated: change in best function value less than options.TolFun.
x =
0.2276 -1.6258 fval =
-6.5511 exitflag =
1
output =
iterations: 2314 funccount: 2341 message: [1x80 char] rngstate: [1x1 struct]
problemtype: 'boundconstraints' temperature: [2x1 double] totaltime: 20.6406
history =
x: [2315x2 double] fval: [2314x1 double] t: [4628x1 double]
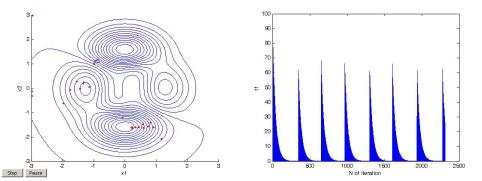
Мы получили тот же результат, однако на это ушло значительно больше итераций и времени решателя. На рис. 27 представлено расположение лучших на текущую итерацию точек от начальной и до оптимальной, обозначенной символом *, и график изменения температуры по x1. По x2 температурный график имеет аналогичный вид. В отличие от предыдущего, в процессе этого поиска переотжиг производился семь раз.
95
Рассмотрим еще один пример применения метода моделирования отжига.
Пример 14.
Найти максимум функции
f 1,5x12e(1 x12 20,25( x1 x2 )2 ) (0,5x1 0,5)4 (x2 1)4 e(2 (0,5x1 0,5)4 ( x2 1)4 )
при условиях
0 x1 4, |
0 x2 3. |
Рис. 27. Поиск минимума функции myfun из точки (–1 1) методом simulannealbnd: слева – лучшие точки, справа – график температуры по x1
Как и выше, записываем целевую функцию в m-файлы в двух вариантах:
function f = multiextr1(x) f=-1.5*x(1)^2*exp(1-x(1)^2-20.25*(x(1)-x(2))^2)-...
(0.5*x(1)-0.5)^4*(x(2)-1)^4*exp(2-(0.5*x(1)-0.5)^4-...
(x(2)-1)^4); end
function f = multiextr1_g(x,y) f=1.5*x.^2.*exp(1-x.^2-20.25*(x-y).^2)+...
(0.5*x-0.5).^4.*(y-1).^4.*exp(2-(0.5*x-0.5).^4-(y- 1).^4)+0.5;
end
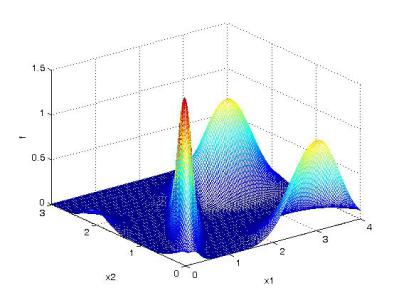
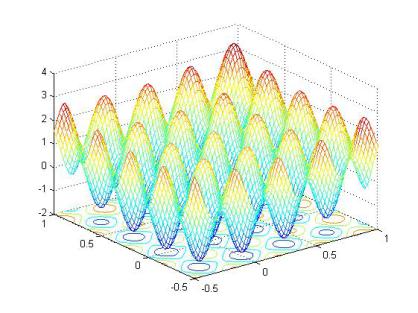
Вид функции multiextr1_g показан на рис. 28, из которого следует наличие у функции многих экстремумов, в частности четырех максимумов.
Для поиска максимума этой функции в программе runsa заменяем имена функций и значения границ переменных на новые, затем запускаем ее с задаваемой начальной точки. Результаты выполнения программы приведены ниже.
96
>> x0=[3 1.4];history=runsa(x0)
Optimization terminated: change in best function value less than options.TolFun.
x =
1.0016 1.0028 fval =
-1.5000 exitflag =
1
output =
iterations: 1601 funccount: 1620 message: [1x80 char] rngstate: [1x1 struct]
problemtype: 'boundconstraints' temperature: [2x1 double] totaltime: 11.7031
history =
x: [1602x2 double] fval: [1601x1 double] t: [3202x1 double]
Рис. 28. Вид функции multiextr1_g
97
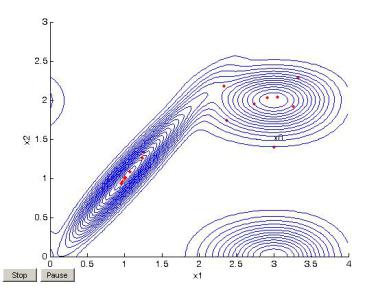
Полученные данные и рис. 29 показывают, что найден глобальный максимум, расположенный на гребне целевой функции. Поиск занял 1601 итерацию. За время поиска переотжиг выполнялся пять раз. Температуры в конечной точке поиска берем из history:
>> [history.t(3201),history.t(3202)] ans =
0.0077 0.0073
Рис. 29. Контуры функции multiextr1_g и расположение лучших точек
Два приведенных примера свидетельствуют о высокой надежности отыскания глобального экстремума методом моделирования отжига. Однако следует помнить, что этот метод не решает задачи с функциональными ограничениями.
Лабораторная работа № 4 Исследование методов прямого поиска и отжига
Задания:
1. Ознакомиться с описанием методов DirectSearch и Simulated Annealing и вызовом соответствующих функций, изучить основные параметры методов.
98
2. Воспроизвести программу из примера 12 и провести ее запуски из одной точки, но при разных алгоритмах прямого поиска; исследовать влияние параметра Complete poll.
3.К задаче из примера 12 добавить условие x1 + x2 –2 и сравнить результаты поиска разными алгоритмами прямого поиска.
4.Методом прямого поиска найти минимумы функции
f1 = (x1 + sin x1) e x12 (1,5–x2)2 при условиях –5 x1 5, –4 x2 5.
5.Воспроизвести программу из примера 14 и исследовать метод моделирования отжига при изменении параметров AnnelingFcn, HybridFcn и начальной температуры.
6.Методом моделирования отжига найти глобальный минимум функции multiextr
f2 = x12 x22 cos(18x1 ) cos(18x2 )
при условиях –0,5 xj 1, j = 1, 2. Выяснить влияние начальной температуры отжига.
Вид функции f2 показан на рис. 30.
Рис. 30. Функция multiextr
7. Сравнить результаты поиска минимума функции f2 методами
DirectSearch и Simulated Annealing.
99
4.5. The Genetic Algorithm
Генетический алгоритм использует терминологию, заимствованную из биологии и отличную от стандартных методов оптимизации. Оптимизируемая функция в генетическом алгоритме называется фит- нес-функцией (fitness function). Каждой итерации алгоритма соответствует набор точек, образующих популяцию (population), а отдельные точки называются особями (individuals). Особь представляется вектором (геномом), состоящим из генов. Популяция представляется матрицей с числом строк, равным размеру популяции, и числом столбцов, равным числу переменных. Значение фитнесфункции особи есть ее метка (score). Последовательности итераций алгоритма соответствует последовательность популяций, называемых поколениями (generations).
Популяция характеризуется разнообразием (diversity), которое оценивается средним расстоянием между особями популяции. Чем оно больше, тем разнообразие выше и тем бόльшая область пространства поиска охватывается популяцией. Для создания нового поколения алгоритм выбирает определенные особи из текущей популяции в качестве родителей (parents) и использует их для создания индивидуальностей нового поколения, называемых потомками или детьми (children). Эти действия выполняются специальными операторами генетического алгоритма. В целом алгоритм включает три этапа:
1.Генерация начальной популяции с помощью датчика случайных
чисел.
2.Создание последовательности новых популяций. Для этого на каждом шаге алгоритм использует особи текущего поколения для образования следующей популяции, выполняя последовательно шаги:
а) помечает каждую особь текущей популяции посредством вычисления значения фитнес-функции;
б) масштабирует полученные метки, преобразуя их к более удобному диапазону значений;
в) выбирает родителей, основываясь на их фитнес-функциях; г) несколько особей с более низкими значениями фитнеса, как
элитные, переводит в новую популяцию;
100
