
Оптимизация в среде MATLAB
..pdf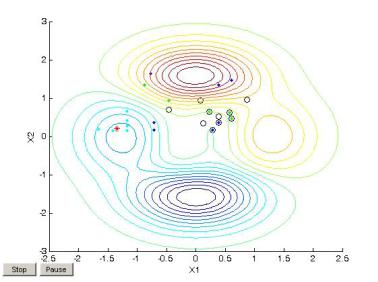
ях хорошо видно, что по крайней мере две особи смежных поколений совпадают, что обусловлено использованием элитизма (по умолчанию две особи элитные).
Добавим в программу обращение к стандартной функции графики gaplotbestf и повторим ее исполнение:
>> options= gaoptimset('PlotFcns',{@gaplotbestf,@plotfun1},… 'PopulationSize',10); [x,fval,exit,output]=ga(@myfun,2,[],[],[],[],[-3 -3],[3 3],[],options) [X,Y]=meshgrid(-3:0.01:3);Z=myfun1(X,Y);contour(X,Y,Z,20); xlabel('X1');ylabel('X2');
Рис. 31. Поиск минимума функции myfun генетическим алгоритмом
Результаты выполнения этой программы представлены на рис. 32 и в следующем отчете:
Optimization terminated: average change in the fitness value less than options.TolFun.
x =
-1.3448 0.2054 fval =
-3.0498 exit =
1 output =
problemtype: 'boundconstraints'
111
rngstate: [1x1 struct] generations: 51 funccount: 520 message: [1x86 char] maxconstraint: 0
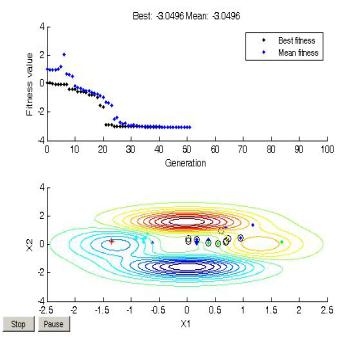
Затраты на поиск того же локального минимума не изменились, но изменилось расположение поколений, кроме конечного (см. рис. 32). На верней части рис. 32 показано изменение двух показателей поколения за весь процесс поиска: среднего в поколении значения фитнесфункции и ее лучшего значения в поколении. Хорошо видно, что минимум получен за 30 поколений, а остальные поколения потребовались для «доводки» точности и достижения условия останова.
Рис. 32. Поиск минимума целевой функции myfun при двух функциях графики
Попробуем найти глобальный минимум дополнительными повторными исполнениями программы. Только на пятой попытке получен искомый результат, о чем свидетельствуют нижеприводимый отчет програмы (рис. 33):
>> options=gaoptimset('PlotFcns',@plotfun1,'PopulationSize',10); [x,fval,exit,output]=ga(@myfun,2,[],[],[],[],[-3 -3],[3 3],[],options)
112
[X,Y]=meshgrid(-3:0.03:3);Z=myfun1(X,Y);contour(X,Y,Z,20); xlabel('X1');ylabel('X2');
Optimization terminated: average change in the fitness value less than options.TolFun.
x =
0.2372 -1.6268 fval =
-6.5503 exit =
1 output =
problemtype: 'boundconstraints' rngstate: [1x1 struct] generations: 57
funccount: 580 message: [1x86 char] maxconstraint: 0
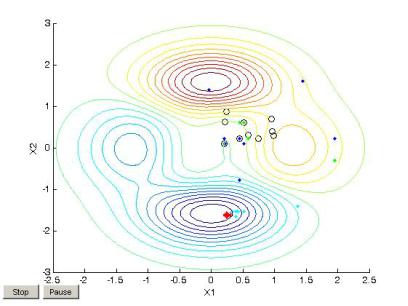
Для достижения глобального оптимума в точке (0,2372 –1,6268) со значением функции цели –6,5503 потребовалось сгенерировать 57 поколений и 580 раз вычислить фитнес-функцию.
Рис. 33. Расположение особей поколений при нахождении глобального минимума
113
Пример 16.
Решить задачу из примера 15 при дополнительном линейном ограничении
0,9x1 – x2 1,2.
Для этого в программу из примера 15 добавим значения входных аргументов: матрицу A = [0,9 –1] и вектор b = [1,2]. После удачной попытки выполнения программы получили
>> options=gaoptimset('PlotFcns',@plotfun1,'PopulationSize',10); [x,fval,exit,output]=ga(@myfun,2,[0.9 -1],[1.2],[],[],[-3 -3],[3 3],[],options) [X,Y]=meshgrid(-3:0.03:3);Z=myfun1(X,Y);contour(X,Y,Z,20); xlabel('X1');ylabel('X2');plot([-2 3],[-3 1.5],'b-','linewidth',2.3);
Optimization terminated: average change in the fitness value less than options.TolFun.
x =
-0.3269 -1.4941
fval =
-3.4532
exit =
1 output =
problemtype: 'linearconstraints' rngstate: [1x1 struct] generations: 62
funccount: 630 message: [1x86 char] maxconstraint: 0
Как следует из рис. 34, генетический алгоритм нашел условный глобальный минимум, который расположен на границе допустимой области в точке (–0,3269 –1,4941) и имеет значение –3,4532. Для этого потребовалось 62 поколения популяций и 630 вычислений целевой функции.
114
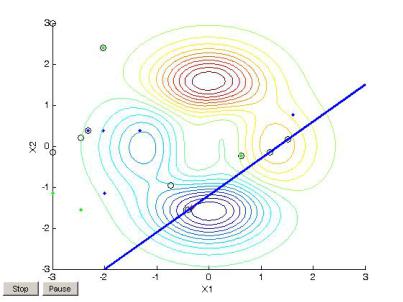
Рис. 34. Поиск минимума функции myfun при линейном неравенстве
Пример 17.
Генетическим алгоритмом найти глобальный максимум функции
f 1,5x12e(1 x12 20,25( x1 x2 )2 ) (0,5x1 0,5)4 (x2 1)4 e(2 (0,5x1 0,5)4 ( x2 1)4 )
при условиях |
|
0 x1 4, |
0 x2 3. |
Эта функция представлена |
m-файлами multiextr1 и mu- |
(см. пример 14), а ее трехмерный вид показан на рис. 28. Решение находим, исполнив программу
>> options=gaoptimset('PlotFcns',@plotfun1,'PopulationSize',10); [x,fval,exit,output]=ga(@multiextr1,2,[],[],[],[],[0 0],[4 3],[],options) [X,Y]=meshgrid(0:0.02:4,0:0.02:3);Z=multiextr1_g(X,Y);contour(X,Y,Z,20); xlabel('X1');ylabel('X2');
Optimization terminated: average change in the fitness value less than options.TolFun.
x =
0.9734 0.9732
fval =
115
-1.4979
exit =
1 output =
problemtype: 'boundconstraints' rngstate: [1x1 struct] generations: 96
funccount: 970 message: [1x86 char] maxconstraint: 0
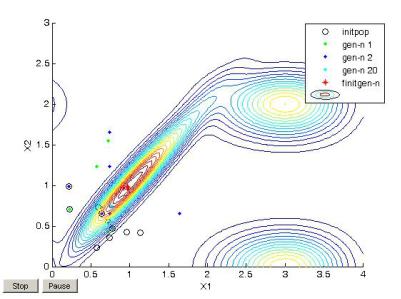
Рис. 35. Поиск глобального максимума функции multiextr1 алгоритмом ga
На рис. 35 хорошо видно, что последнее поколение особей находится в окрестности глобального максимума. Несмотря на наличие гребня, максимум локализован достаточно точно: координаты оптимума (0,9734, 0,9732 ) близки к точным (1 1), а значение целевой функции в нем 1,4979 практически равно точному 1,5.
4.6. Сравнительная характеристика решателей
Эффективность методов оценивается скоростью сходимости. GlobalSearch и MultiStart дают быструю сходимость к локальному оптимуму гладкой задачи благодаря использованию производ-
116
ных. Для patternsearch доказана сходимость к локальному экстремуму, но скорость сходимости ниже, чем у методов, использующих производные. Для генетического алгоритма сходимость не доказана. Сходимость к глобальному оптимуму доказана для simulannealbnd для задач с границами на переменные при условии очень медленного охлаждения, т.е. низкой скорости.
Область применения решателей в зависимости от типа задачи и способа вычислений представлена в следующей таблице.
Цель и способ |
Гладкие функции |
Негладкие функции |
|
вычислений |
|||
|
|
||
Одно локальное решение |
Функции Optimiza- |
fminbnd, pattern- |
|
|
tion Toolbox |
search, fmin- |
|
|
|
search, ga, simu- |
|
|
|
lannealbnd |
|
Много локальных |
GlobalSearch, |
|
|
решений |
MultiStart |
|
|
Одно глобальное |
GlobalSearch |
patternsearch, ga, |
|
решение |
Multi-Start, |
simulannealbnd |
|
|
patternsearch, ga, |
|
|
|
simulanealbnd |
|
|
Одно локальное решение |
MultiStart, функции |
patternsearch, ga |
|
с распараллеливанием |
Optimization Tool- |
|
|
|
box |
|
|
Много локальных решений |
MultiStart |
|
|
с распараллеливанием |
|
|
|
Одно глобальное решение |
MultiStart |
patternsearch, ga |
|
с распараллеливанием |
|
|
Лабораторная работа № 5 Генетический алгоритм
Задания:
1.Усвоить схему генетического алгоритма и назначение основных параметров популяции, алгоритма и функций графики, понять работу функций отбора, кроссовера и мутации.
2.Применить генетический алгоритм к функции multiextr1 на
области –3 xj 4, j = 1, 2 с целью нахождения глобальных максимумов при нескольких размерах популяции.
117
3. Найти глобальный максимум функции myfun. Построить зависимость оптимального значения целевой функции от доли кроссовера при одном размере популяции. Для получения соответствующих данных можно применить цикл
record=[];
for n=0.05:.05:1
options = gaoptimset('CrossoverFraction',n, …); [x fval]=ga(…,options);
record = [record; fval]; end
4.Найти глобальный максимум функции myfun в границах –3 xj 3,
j = 1, 2 и при дополнительных ограничениях –4x1 + 5x2 7, 3x1 + 4x2 9 принесколькихзначенияхчислаэлитныхособей.
5.Исследовать влияние вида кроссовера (из числа стандартных)
на поиск минимумов функции |
f x2 |
x2 |
cos(8x ) cos(8x |
2 |
) |
|
1 |
2 |
1 |
|
e( x1 0,5x2 ) при условиях –0,5 xj 1, j = 1, 2.
6.Факультативно: исследовать эффективность генетического алгоритма на тестовой многоэкстремальной функции Растригина второго порядка
f20 x12 x22 10(cos(2 x1) cos(2 x2 )) при условиях –1 xj 1.
7.Факультативно: написать собственный кроссовер и опробовать его на многоэкстремальной функции.
118
5. МНОГОКРИТЕРИАЛЬНАЯ ОПТИМИЗАЦИЯ
Во многих прикладных задачах оптимизации цель описывается не одной, а несколькими функциями (критерями), и в этом случае говорят о векторной оптимизации. При этом оптимальное решение такой задачи в традиционном понимании не имеет смысла. Лицо, принимающее решения (ЛПР), стремится найти некоторое компромиссное по целевым функциям решение, удовлетворяющее его субъективным представлениям (предпочтениям) о желаемом результате. В теории многокритериальной оптимизации показано, что искать компромиссное решение следует только среди паретовских решений. Решение X* оптимально по Парето, если не существует другого допустимого решения X, в котором значение хотя бы одного критерия было лучше, а других не хуже, чем в X*. Иначе говоря, паретовские решения являются недоминируемыми (noninferior) или неулучшаемыми. Методы многокритериальной оптимизации ориентированы на предоставление ЛПР паретовских или, по крайней мере, слабопаретовских решений. Ниже рассматриваются функции MATLAB, реализующие некоторые из таких методов.
5.1. Функция gamultiobj
Эта функция входит в состав пакета Global Optimization. Она пытается создать множество парето-оптимальных решений минимизацией многомерной целевой функции. Допускается наличие границ на переменные, а также линейных неравенств и равенств, но нелинейные ограничения неприемлемы. Для минимизации используется контролируемый генетический алгоритм с элитизмом, его отличие от ga невелико. Алгоритм с элитизмом всегда предпочитает особи с лучшим значением фитнес-функции (ранга), а при контролируемости предпочитаются также особи, которые могут помочь в увеличении разнообразия популяции, даже если они имеют более низкие значения фитнеса. Разнообразие особей улучшает сходимость к множеству Парето, оно обеспечивается контролем числа элитных особей. Для этого используются два параметра, отличных от имеющихся в ga. Параметр ParetoFraction ограничивает число особей на границе Парето (элитных членов), определяя долю популяции на лучшей границе Парето, удерживаемую в процессе оптимизации. При одной границе Па-
119
рето этот параметр игнорируется. Второй параметр, DistanceFcn, задает функцию расстояния, способствующую созданию разнообразия на границе посредством предпочтения особям, которые относительно далеки от границы Парето.
Изменение параметров gamultiobj выполняется через функцию gaoptimset. Большинство параметров ga и gamultiobj идентичны (прил. 6). Два отличительных параметра упомянуты выше. Параметр DistanceMeasureFcn определяет функцию, которая задает меру расстояния между особями. Кроме того, для отображения границы Парето в случае двумерной целевой функции, т.е. зависимости между функциями на найденном множестве Парето, имеется функция графики @gaplotpareto, устанавливаемая параметром PlotFcn. Отметим другие отличия от алгоритма ga. Прежде всего обратим внимание на то, что способ отбора родителей не может быть выбран: используется только турнирный вариант, причем число турниров должно быть равно числу целевых функций. Определение элитных особей обеспечивается сортировкой популяции, при которой недоминируемые особи размещаются выше доминируемых. В gamultiobj отсутствует выбор функции масштабирования, а в качестве непустого значения HybridFcn может быть только функция fgoalattain, о которой речь пойдет в следующем разделе. Наконец, в рассматриваемом алгоритме не используется параметр времени StallTimeLimit, исчерпание которого приводит к остановке ga.
При применении gamultiobj сначала устанавливаются необходимые значения параметров, и затем вызывается сама функция. Как и для других функций оптимизации, имеются разные варианты вызова gamultiobj, зависящие от описания решаемой задачи (перечня входных аргументов) и требуемых результатов (выходных аргументов). Синтаксис вызовов gamultiobj в командном окне представлен ниже.
X = gamultiobj(FITNESSFCN,NVARS)
X = gamultiobj(FITNESSFCN,NVARS,A,b)
X = gamultiobj(FITNESSFCN,NVARS,A,b,Aeq,beq)
X = gamultiobj(FITNESSFCN,NVARS,A,b,Aeq,beq,LB,UB) X = gamultiobj(FITNESSFCN,NVARS,A,b,Aeq,beq,LB,...
UB,options)
X = gamultiobj(problem) [X,FVAL] = gamultiobj(...)
[X,FVAL,EXITFLAG] = gamultiobj(...)
120
