
Теоретическая механика избранные задачи студенческих олимпиад ПНИПУ
..pdf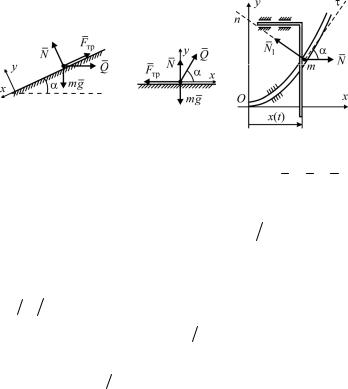
направлении оси |
x |
и m ax mg sin Q cos f N . Если же |
||||||||
|
mg x Qx |
|
f N , то точка останется неподвижной и ax 0 . |
|||||||
|
|
|||||||||
|
|
|
|
(1 |
f k)sin (k f )cos , |
если |
|
f , |
||
|
Ответ: ax g |
|
f k)sin (k f )cos , |
если f , |
||||||
|
(1 |
|||||||||
|
|
|
|
|
0 |
если |
|
|
|
f , |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
где (sin k cos ) (cos k sin ) .
(cos k sin ) .
Д6. Ответ: при tg (2k  m)
m) (1 exp( 2k
(1 exp( 2k 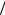 m)) .
m)) .
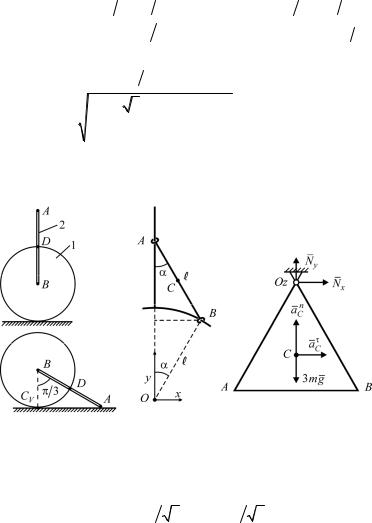
К задаче Д5 К задаче Д7 К задаче Д11
Д7. Уравнение движения точки: m a mg N Q Fтр . Проецируя это уравнение на ось y, найдем N mg k t sin ; следователь-
но, момент отрыва точки от плоскости tотр mg |
k sin . Проецируя |
|||||||
уравнение движения точки на ось x, найдем: |
m ax kt cos Fтр . |
|||||||
До тех |
|
пор пока |
kt cos f N |
(при |
0 t t1 , где |
|||
t1 fmg |
k |
cos f sin tотр ), |
ax 0 . |
При |
t1 t tотр |
|||
m ax kt cos f N , откуда ax fg t1 t t1 . Таким образом, |
||||||||
|
|
|
0, |
если |
0 t t |
, |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x |
t t1 , |
если |
t1 t |
tотр. |
|
|
|
|
fg t1 |
|
|||||
|
|
|
|
|
|
|
|
|
Интегрируя последнее соотношение с учетом начальных условий, получим
81

|
|
|
0, |
|
|
|
если |
|
0 t t1, |
|
|
|||||||
Ответ: x(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
3 |
, |
если |
t1 t tотр, |
|
|
||||||||
|
|
fg (6t1) t |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где t1 fmg k |
cos f sin . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Д8. Ответ: |
x(t) (ma c)cos( |
c m t) at 2 2 ma c . |
|
|
||||||||||||||
Д9. Уравнение |
движения |
точки |
|
в |
проекции |
на |
ось |
x: |
||||||||||
m dV dt k xV . Учитывая, что |
dV dt VdV dx , |
разделяя пере- |
||||||||||||||||
менные и интегрируя, найдем |
скорость точки как функцию x: |
|||||||||||||||||
V V0 k x2 (2m) . Далее, dx dt V0 k x2 |
|
(2m) . Разделяя пере- |
||||||||||||||||
менные и интегрируя, |
найдем: arth x |
x1 t t1 , |
где |
x1 |
2mV0 |
k |
||||||||||||
(расстояние, которое точка пройдет до остановки), t1 |
2m (kV0 ) . |
|||||||||||||||||
Ответ: x(t) x1 th t t1 , где |
x1 |
|
2mV0 |
|
k , t1 |
|
2m (kV0 ) . |
|
||||||||||
Д10. Ответ: t1 m (2kV1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Д11. Уравнение движения точки: |
|
|
|
|
|
|||||||||||||
m a N |
N1 . Проецируя это |
|||||||||||||||||
уравнение на оси x и y, найдем mx N N1 sin , |
my N1 cos . |
|||||||||||||||||
Учитывая, что x u t , |
y k x2 ku 2t 2 , |
tg y 2 k x 2 ku t и ис- |
||||||||||||||||
ключая N1 , получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: N(t) 4m k 2u3t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Д12. Ответ: s V0 |
kg sin ; |
t1 ( 2) |
|
kg sin . |
|
|
|
|||||||||||
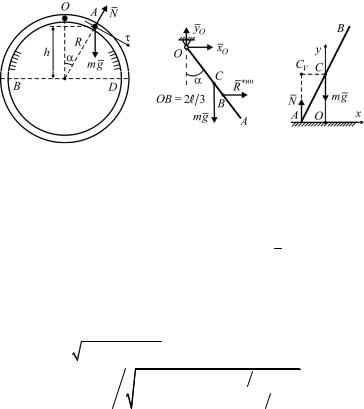
Д13. Модуль ускорения точки a |
a2 |
a2 |
. Уравнение дви- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
. Проецируя это уравнение на ось |
, |
|||||||||||||||
жения точки m a m g N |
||||||||||||||||||
найдем a g sin g |
1 h R 2 . Далее, an V 2 R . Найдем V 2 |
|||||||||||||||||
из закона сохранения полной энергии: mV 2 |
2 mgh mgR . Отсюда |
|||||||||||||||||
V 2 2g(R h) , |
следовательно, an 2g 1 h R . После преобразо- |
|||||||||||||||||
ваний получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: a(h) g |
1 h R 5 3h R . |
|
|
|
|
|
|
|
|
|
||||||||
82 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д14. Ответ:
если exp(kL) 2 , то точки никогда не встретятся;
если exp(kL) 2 , то t1 (exp(kL) 1) (V0k(2 exp(kL))) .
(V0k(2 exp(kL))) .
К задаче Д13 |
К задаче Д15 |
К задаче Д17 |
Д15. Перейдем в систему |
отсчета, связанную со стержнем. |
|
В этой системе отсчета стержень неподвижен, а к действующим на него силам следует добавить переносные силы инерции. Система
сил инерции приводится к равнодействующей R ин , показанной на рисунке. Составим уравнение равновесия стержня:
mO mg  2 sin R ин 2
2 sin R ин 2  3 cos 0 .
3 cos 0 .
Учитывая, что R ин maC (m 2  2)sin , получаем Ответ: 3g
2)sin , получаем Ответ: 3g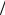 (2 cos ) .
(2 cos ) .
Д16. Ответ: 2 |
2g |
|
8c m |
|
|
|
. |
||
3(R r) |
3(1 (1 2r R)2 ) |
|||
Д17. Согласно закону сохранения полной энергии, mVC2  2 JCz 2
2 JCz 2  2 m g yC mg ,
2 m g yC mg ,
где JCz m 2  3 . Так как внешние силы, действующие на стержень,
3 . Так как внешние силы, действующие на стержень,
не имеют составляющих по оси x и в начальный момент времени скорости точек стержня равнялись нулю, то при движении стержня xC const . Тогда
83

V |
C |
y |
C |
, V |
CC y |
2 y2 . |
|||
|
|
|
C |
V |
C |
|
C |
||
С учетом этих соотношений находим |
|
|
|
||||||
|
|
y2 |
6g |
1 yC 1 yC2 |
2 |
. |
|||
|
|
|
|
||||||
|
|
C |
|
|
|
4 3 y2 |
2 |
|
|
|
|
|
|
|
|
C |
|
|
|
Проецируя теорему о движении центра масс стержня на ось y, получим N mg myC . Дифференцируя по времени выражение для
y |
2 |
, найдем |
y |
как функцию |
y |
C |
; подставляя результат в выражение |
||||
|
C |
|
C |
|
|
|
|
|
|
|
|
для N, получим |
|
|
|
|
|
|
|
|
|||
|
|
Ответ: |
N( yC ) mg |
1 3 1 yC |
2 |
. |
|
||||
|
|
4 3 yC2 |
2 2 |
|
|||||||
|
|
|
|
|
|
|
|||||
|
|
Д18. Ответ: M B m sin ( 2 cos g) . |
|
||||||||
|
|
Д19. Согласно закону сохранения полной энергии |
|||||||||
|
|
|
|
T нач Пнач |
T кон T кон Пкон |
||||||
|
|
|
|
|
2 |
|
|
1 |
|
2 |
2 |
(потенциальная энергия диска 1 не меняется и ее можно считать
равной нулю). Здесь T нач 0 , П2нач mghDнач |
2mgR |
(высота от- |
||||||
считывается |
от |
уровня |
плоскости), |
T кон mV 2 |
2 J 2 |
2 , |
||
|
|
|
|
|
1 |
B |
1 |
|
T2кон mVD2 |
2 J 2 2 2 , |
П2кон mghDкон mgR 2 . Учитывая, |
что |
|||||
J1 mR2 2 , |
J2 m 2R 2 12, |
VB BCV R, |
VD DCV R , |
|||||
находим |
18 |
17 g |
R . Далее, VA ACV R |
3 . |
|
|||
Ответ: VA |
54 17 gR . |
|
|
|
|
|||
Д20. Ответ: max |
(3g |
(5 ))( 10 1) . |
|
|
|
|||
Д21. Стержень с колечками можно рассматривать как твердое |
||||||||
тело массой |
m m1 2m 2 ; центр масс C этого тела – в середине |
|||||||
стержня, момент |
инерции |
JCz m1 2 |
12 2m 2 2 2 . Согласно |
|||||
закону сохранения полной энергии |
|
|
|
|
||||
84 |
|
|
|
|
|
|
|
|
mVC2  2 JCz 2
2 JCz 2 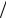 2 mghC mghC0 mg 3
2 mghC mghC0 mg 3  2
2
(высота отсчитывается от уровня точки O). Для произвольного зна-
чения угла |
|
A |
|
|
B |
|
|
|
|
|
|
|
|
|
C |
|
A |
|
B |
|
|
|
|
|
|
|
|
|
|||
|
x |
C |
(x |
x |
) |
2 |
2 |
sin |
, y |
(y |
y |
) |
2 |
2 |
cos |
. |
|||||||||||||||
, |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
||||||||||||||||
Поэтому |
|
VC2 xC2 |
yC2 |
( 2 |
4) 2 (1 8sin2 ) , |
hC yC 3 2 cos . |
|||||||||||||||||||||||||
Находя |
|
из |
|
закона |
сохранения |
энергии |
|
и |
учитывая, |
что |
|||||||||||||||||||||
VA yA 2 sin , |
6 , получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Ответ: VA |
|
9(2 |
3)g (m1 2m 2 ) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
5m1 12m 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Д22. Ответ: |
n |
R 02 (1 f 2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
8 g f (1 f ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
К задаче Д19 |
К задаче Д21 |
К задаче Д23 |
|
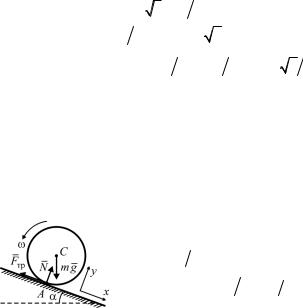
Д23. Согласно теореме о движении центра масс, в поло- |
|||
жении, когда сторона |
AB горизонтальна, 3m aCn N y 3mg , |
||
3m aC N x . Здесь aCn 2 |
3 , aC |
3 0 (так как в дан- |
|
85
ном положении достигает максимума), – длина стержня. Согласно закону сохранения полной энергии
Tнач Пнач Tкон Пкон ,
где Tнач 0 , |
Пнач |
3mg 2 |
(высота отсчитывается от уровня |
оси O ), Tкон J z 2 2 , |
Пкон |
3mg . Учитывая, что |
|
|
J z 2m 2 3 m 2 12 m 3 2 2 |
||
(для стороныAB использованатеоремаГюйгенса–Штейнера), получим Ответ: N 5mg .
Д24. Ответ: 1 arccos (2 3) .
3) .
Замечание: строго говоря, нужно еще проверить, что реакция горизонтальной плоскости N y 0 при 0 1 ; можно показать,
что это условие выполнено.
|
Д25. Дифференциальные уравнения |
дви- |
|
|
жения диска: |
|
|
|
m dVCx dt mg sin Fтр , 0 N mg cos , |
||
|
mR2 2 d dt FтрR . |
|
|
К задаче Д25 |
Кроме того (до момента |
прекращения |
про- |
скальзывания), Fтр f N . |
Интегрируя уравне- |
||
ния с учетом начальных условий, найдем
VCx g sin f cos t , 0 2 f gt cos  R .
R .
Далее, VAx VCx R 0 R g sin 3 f cos t . Проскальзывание прекратится при VAx 0 .
Ответ: если tg 3 f , то T 0 R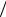 g
g  3 f cos sin ;
3 f cos sin ;
если tg 3 f , топроскальзывание никогданепрекратится. Д26. Ответ: M (t) mR2k 2t 4 .
4 .
86
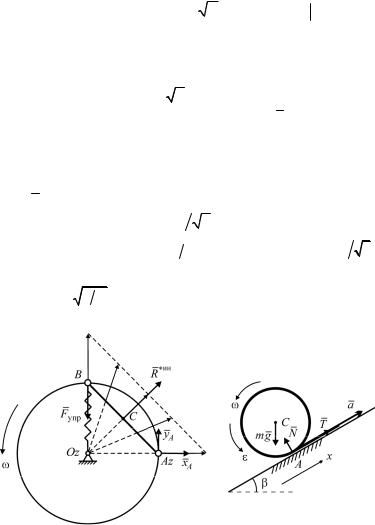
Замечание: соотношение k и условие t 0 0 выполнены также в случае M (t) 0 , который, однако, отвечает непод-
вижному, а не вращающемуся (как указано в условии задачи) диску. Д27. На рисунке показано взаимное расположение стержня и
диска, соответствующее L r 2 и r . На стержень действуют реакция шарнира A и сила упругости пружины Fупр (сила тяжести и
нормальная реакция диска уравновешиваются). Присоединяя к этим силам д’Аламберовы силы инерции, рассмотрим равновесие сил. Система сил инерции – сходящаяся и приводится к равнодейст-
вующей R ин . Уравнение равновесия сил
mAz R ин r |
2 Fупрr 0 . |
Учитывая, что Fупр с( 0 ) cr 2 |
и R ин m 2 CO m 2r 2 , по- |
лучаем |
|
Ответ: c m . |
|
К задаче Д27 |
К задаче Д29 |
Д28. Ответ: при F mg 3 .
3 .
87

Д29. Дифференциальные уравнения движения диска: |
|
||||||||||||||||||||||
|
|
m aC x m g sin T , |
|
mR2 |
2 TR |
|
|||||||||||||||||
(T – сила натяжения нити). Кроме того, дифференцируя по времени |
|||||||||||||||||||||||
кинематическое соотношение |
|
VAx VCx |
|
|
R (A – точка сопри- |
||||||||||||||||||
косновения диска с плоскостью), |
получаем a aCx |
R . Из по- |
|||||||||||||||||||||
лученных уравнений находим aCx и aC |
|
aCx |
|
. |
|
||||||||||||||||||
|
|
|
|||||||||||||||||||||
Ответ: aC |
|
a 2g sin |
|
|
3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Д30. Ответ: |
(g r)ctg . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Д31. Дифференциальное |
уравнение |
вращательного |
движения |
||||||||||||||||||||
стержня: J |
z |
|
|
|
|
z |
m |
|
2 |
|
|
2 |
|
3 . Дифференцируя по време- |
|||||||||
|
M ( ) , где J |
|
|
|
|
|
|
|
|
||||||||||||||
ни равенство |
|
|
CB tg , |
|
получим |
u cos2 , |
откуда |
||||||||||||||||
u cos2 . |
Дифференцируя по времени последнее равенство |
||||||||||||||||||||||
и подставляя |
из него же, найдем 2 u 2 sin cos3 . |
||||||||||||||||||||||
Ответ: M ( ) 8mu 2 |
|
|
3 sin cos3 . |
|
|
|
|
||||||||||||||||
Д32. Ответ: |
|
2F0 (mR) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Д33. Кинетическая энергия системы |
|
|
|
|
|
|
|
||||||||||||||||
|
T J 2 |
2 m V 2 |
2 J |
2 |
2 |
2 B 2 2 , |
|
||||||||||||||||
|
|
|
1 1 |
|
2 |
C 2 |
|
|
|
|
|
2 |
|
3 |
|
||||||||
где J1 m1R12 2 , |
|
J2 m2R22 2 , |
1 2 3 R1 , VC2 3 , 2 3 R2 , |
||||||||||||||||||||
R1 R2 , B 2 2m1 3m 2 |
2 2J1 2 |
|
R12 2 3m 2 |
2m1 . |
|||||||||||||||||||
Сумма мощностей внешних сил N e |
M 3 3 M1 1 Q 3 , где |
|||||
Q M 3 2 R1 M1 . Из теоремы об изменении кинетической энер- |
||||||
гии следует, что 3 Q B . Так как |
1 |
3 k , то R1 k 2 . Да- |
||||
лее, m 2 m1 R22 R12 |
|
R1 1 2 . Окончательно получаем |
||||
Ответ: 3 |
|
M 3 |
k M1 |
|
. |
|
J1k 2 |
1 3(k 2)2 16 |
|
||||
|
|
|
||||
88 |
|
|
|
|
|
|
Д34. Ответ: отрезок прямой x  2 ,
2 ,  2 y 0 .
2 y 0 .
Д35. Так как проекции внешних сил на горизонтальную плос-
кость равны нулю и |
при t 0 система была неподвижна, то при |
t |
0 центр масс С системы остается неподвиж- |
|
ным. Так как AB R const , то точки A и B опи- |
|
сывают окружности радиусами R 2 с центром в |
|
C и в каждый момент времени имеют равные по |
|
модулю и противоположно направленные скоро- |
|
сти. Тогда VB VBr VBe Vr VA R VA ( – |
К задаче Д35 |
угловая скорость диска), откуда (2VA Vr ) R . |
|
Далее, моменты внешних сил относительно лю- |
бой вертикальной оси равны нулю, поэтому (с учетом неподвижности системы при t 0 и неподвижности С при t 0 ) при t 0 кинетический момент системы относительно такой оси равен нулю.
Выберем ось Az, тогда LAz mR2  2 mVB R 0 ; подставляя сюда найденное выше выражение для и учитывая, что VB VA , получим
2 mVB R 0 ; подставляя сюда найденное выше выражение для и учитывая, что VB VA , получим
Ответ: VA (t) Vr (t) |
4 . |
|
|
|
|
|
|
|||
|
|
|
|
Д36. Ответ: при f |
3 17 . |
|
|
|||
|
|
|
|
Д37. Добавив к силам, действующим на |
||||||
|
систему, |
д’Аламберовы |
|
|
ин , |
|||||
|
силы инерции F |
|||||||||
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
ин , F |
ин |
, получим уравновешенную систему |
|||||
|
F |
|||||||||
|
|
e |
|
Cor |
|
|
|
|
||
|
сил. Уравнения равновесия: |
|||||||||
|
|
|
|
mx mgRsin Frин 3R 2 sin |
||||||
|
|
|
|
|
|
Feин 3R 2 Rcos YB 3R 0 , |
||||
|
|
|
my FCorин 3R 2 R cos X B 3R 0 . |
|||||||
|
Учитывая, что Fин mu2 |
R, F ин m 2Rsin , |
||||||||
|
|
|
|
|
|
|
r |
e |
||
К задаче Д37 |
Fин |
2m ucos , из этих уравнений получаем |
||||||||
|
Cor |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
89 |
||

Ответ: X B m u cos 1 (2 3)cos ,
3)cos ,
YB msin g 3 u 2
3 u 2  2R 2 R (1
2R 2 R (1 2) (1
2) (1 3) cos .
3) cos .
Д38. Ответ: (3 (5 2))(V0
(5 2))(V0  R) .
R) .
Д39. Согласно закону сохранения кинетического момента
m1a2 m 2 x2 m1a2 m 2b2 0 .
Согласно закону сохраненияполнойэнергии(в данном случае П 0 )
m1a2 2  2 m 2 x2 2 Vr2
2 m 2 x2 2 Vr2  2 m1a2 m 2b2 02
2 m1a2 m 2b2 02  2 .
2 .
Выражая из первого равенства и подставляя во второе, получим
Ответ: Vr (x) |
m1a2 |
m 2b2 x2 b2 |
|
0 . |
|
|||||
m1a2 m 2 x2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
||
Д40. |
Ответ: |
|
|
|
2m 2 |
(T (J m 2 )) . |
|
|
|
|
|
|
|
|
|
||||||
Д41. |
Уравнение |
поступательного |
|
движения |
груза |
|||||
m1x T m1g , где T – сила натяжения нити. Уравнение вращатель-
ного движения диска m2 R2  2 kt TR . Учитывая, что x R ,
2 kt TR . Учитывая, что x R ,
и исключая T, найдем m1 m2  2 x kt
2 x kt R m1g . Интегрируя один
R m1g . Интегрируя один
раз это уравнение с использованием начальных условий, найдем скорость груза; приравняв ее нулю, найдем время до остановки; интегрируя уравнение второй раз и подставляя найденное время до остановки, получим
Ответ: s |
2m31g 3R2 |
||
|
. |
||
3k 2 m1 m2 2 |
|||
Д42. |
Ответ: нить не будет провисать при 2 Rr . |
||
Д43. |
Согласно закону сохранения количества движения |
||
|
|
m1V1 m2 (V2e V2r cos ) 0 , |
|
где V2e V1 . Согласно закону сохранения полной энергии
90
