
Демонстрационный курс лекций по начертательной геометрии Модуль 1. То
.pdf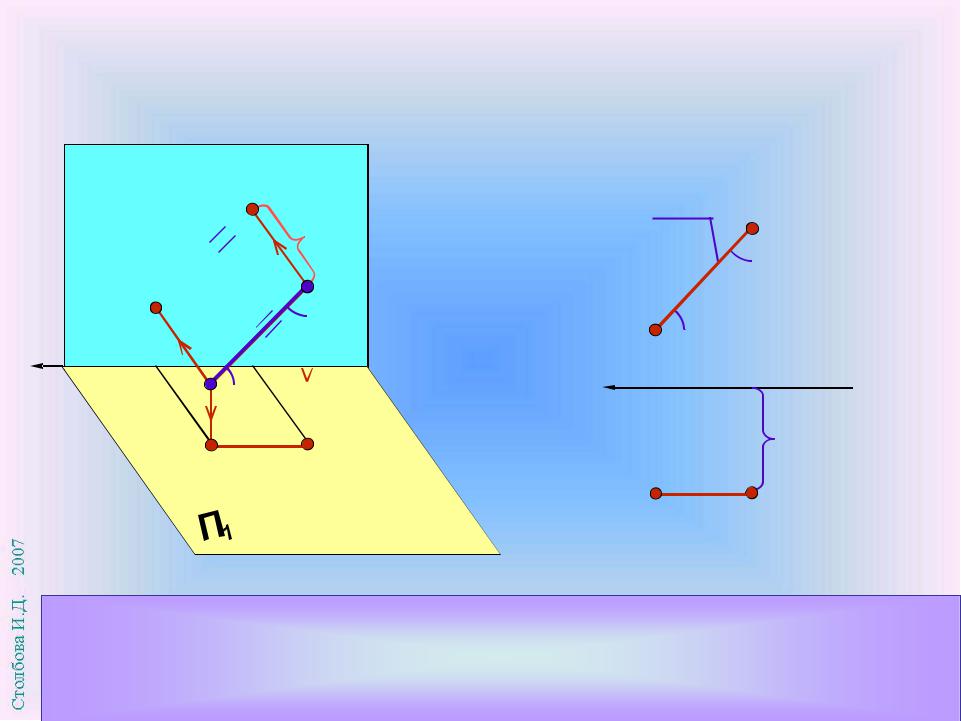
Прямые уровня: |
фронталь (f П2) |
Пространственная картина |
Комплексный чертеж |
|
П2 |
В2 |
|
|
|
|
|
||
|
|
|
|
|
y=cons |
||||
|
|
f2 |
|
|
|
|
|||
|
А2 |
|
f |
|
tB |
||||
|
|
|
|
|
|||||
x |
|
A |
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
f1 |
|
|
|
|
|
|
|
А1 |
|
B1 |
|||||
|
|
|
|
|
|||||
x
н.в. В2
f2 |
|
|
|
|
|||||
А |
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f1 |
y=cons |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
А1 |
|
|
|
|
|
Bt1 |
|||
|
|
|
|||||||
|
|
|
|
|
|
||||
|
|
||||||||
Все точки прямой АВ равноудалены от фронтальной плоскости проекций П2 и имеют одинаковую координату y (y= const). Горизонтальная проекция фронтали А1 В1 параллельна оси х. Фронтальная проекция фронтали А2 В2 , углы и изображаются в натуральную величину на П2
Прямые уровня: профильная прямая (р П3)
Пространственная картина Комплексный чертеж
П2 |
|
|
|
z |
|
|
z |
|
В3 н.в. |
|
В |
|
|
В3 |
|
|
В2 |
|
|||
|
р2 |
B |
р3 |
|
р |
|
|
р |
||
|
2 |
|
|
2 |
|
|
3 |
|||
x |
А2 |
|
x=const |
|
А2 |
|
|
А |
||
р |
|
|
x |
O |
|
3 |
||||
|
B1р |
|
А3 |
B |
|
y3 |
||||
|
A |
|
|
р1 |
|
|
|
|||
|
|
1А1 |
|
y |
|
А11x=cons |
y |
1 |
|
|
|
|
|
|
|
|
t |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
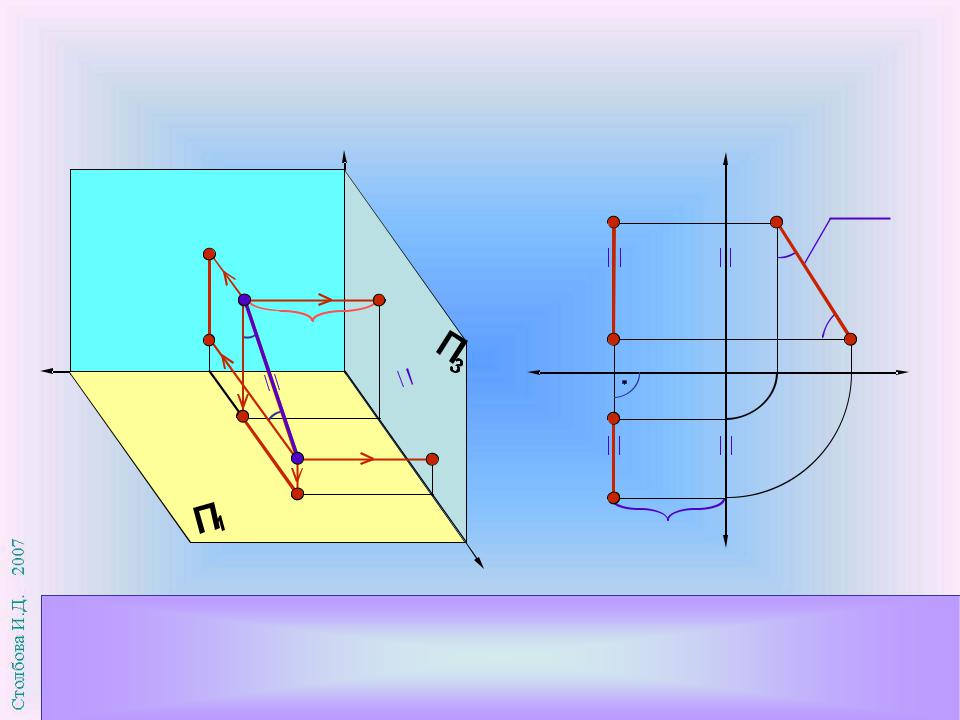
Все точки прямой АВ равноудалены от профильной плоскости проекций П3 и имеют одинаковую координату х (х= const). Горизонтальная А1 В1 и фронтальная А2 В2 проекции прямой перпендикулярны оси х.
Профиль-ная проекция А3 В3 , углы и имеют натуральную величину
Горизонтально проецирующая прямая ( П1)
Пространственная картина |
Комплексный чертеж |
П2 В2
 B
B
А2
x
 A
A
(А1) B1
В2
н.в.
А2 
x
(А1) B1
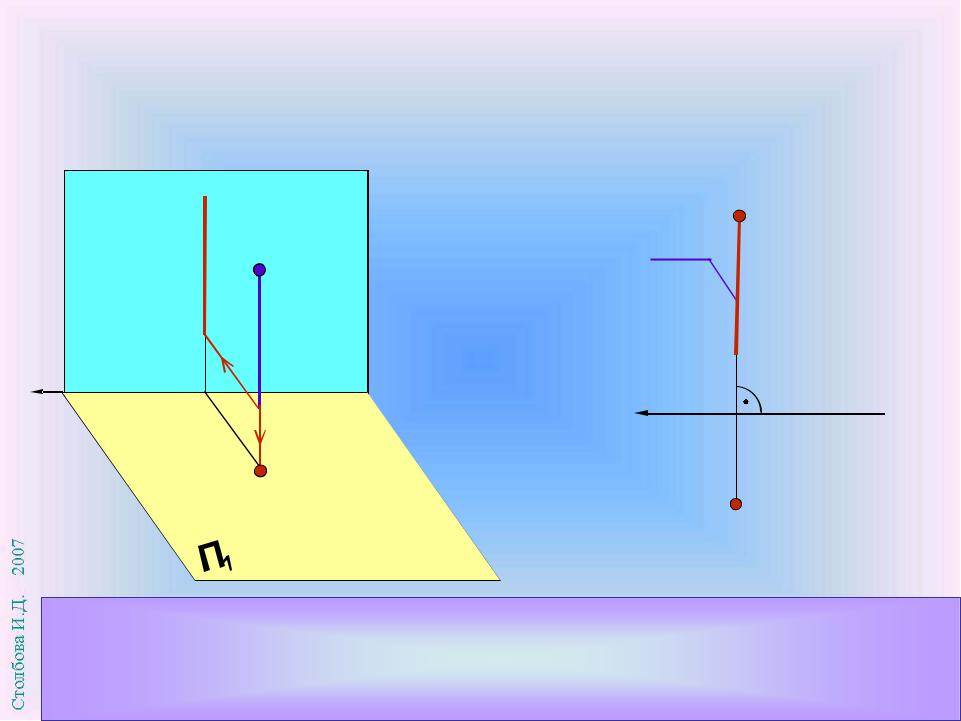
Прямая перпендикулярна П1 , поэтому ее горизонтальная проекция А1 В1 вырождается в точку. Относительно П2 и П3 прямая параллельна и изображается на этих плоскостях проекций в натуральную величину. Проекция А2 В2 перпендикулярна оси координат х
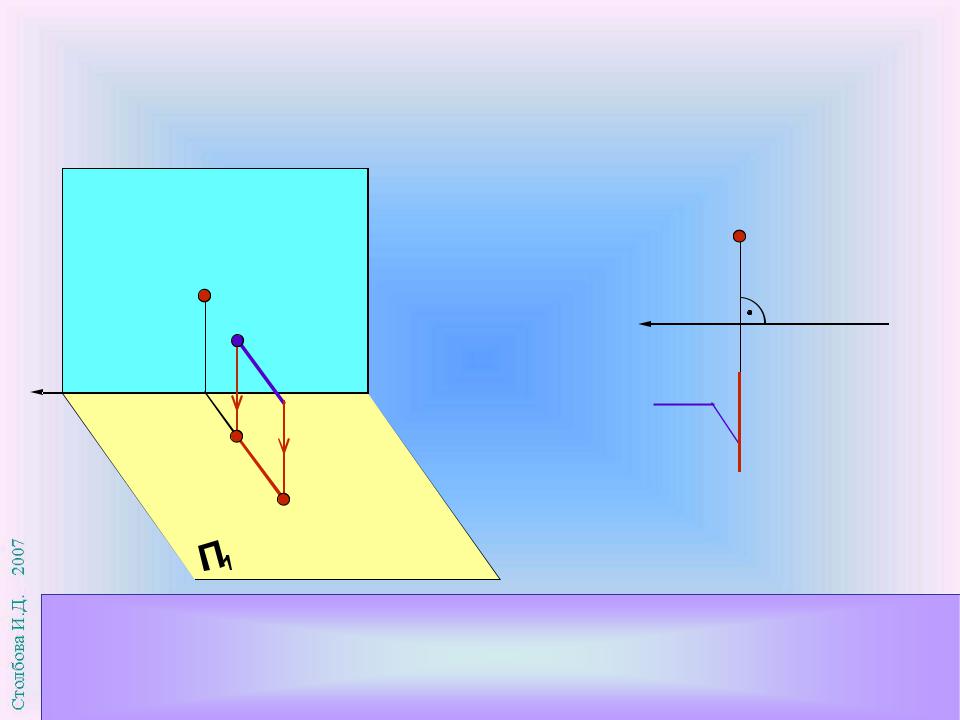
Фронтально проецирующая прямая ( П2)
Пространственная картина |
Комплексный чертеж |
П2
(В2 ) А2
 B
B
x
 A
A
B1
А1
x
(В2 ) А2
н.в.  B1
B1
 А1
А1
Прямая перпендикулярна фронтальной плоскости проекций П2 и параллельна П1 и П3 . Фронтальная проекция А2 В2 вырождается в точку. На П1 и П3 прямая проецируется в натуральную величину. Проекция А1 В1 перпендикулярна оси координат х
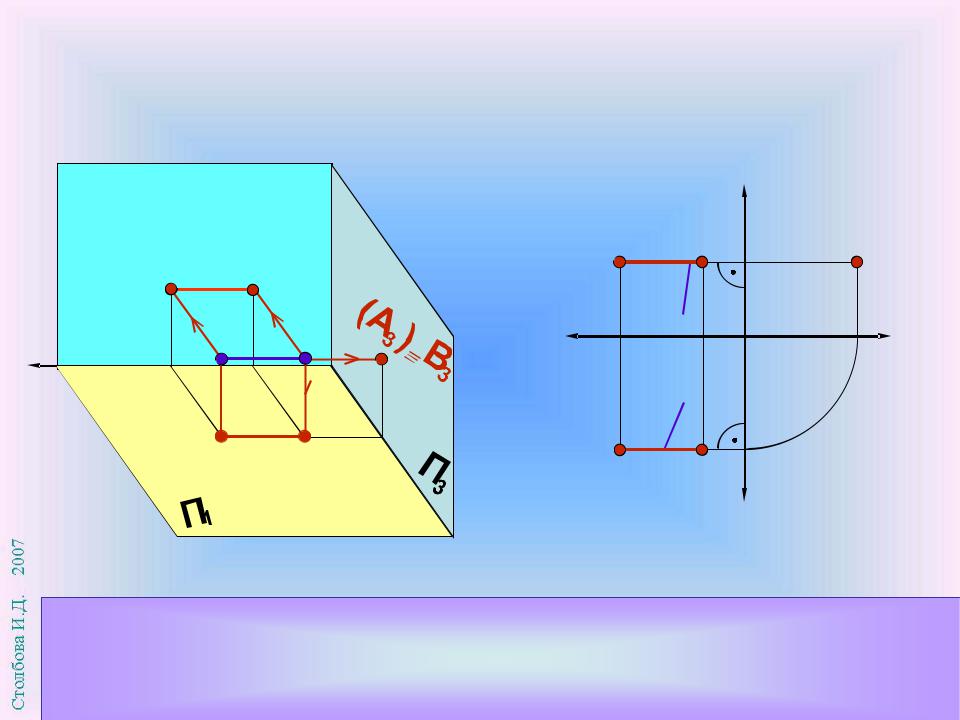
Профильно проецирующая прямая ( П3)
Пространственная картина
 z
z
П2
В2 А2
x
 B
B  A
A
B1 А1
 y
y
Комплексный чертеж
z
B2 А2 (A3) B3
|
н.в. |
|
|
x |
|
O |
y3 |
|
н.в. |
|
|
|
|
|
|
B1 А1 y1
Прямая перпендикулярна П3 , ее профильная проекция А3 В3 вырождается в точку. Относительно П1 и П2 прямая параллельна, на этих плоскостях ее проекции имеют натуральную величину. Горизонтальная и фронталь-ная проекции прямой перпендикулярны
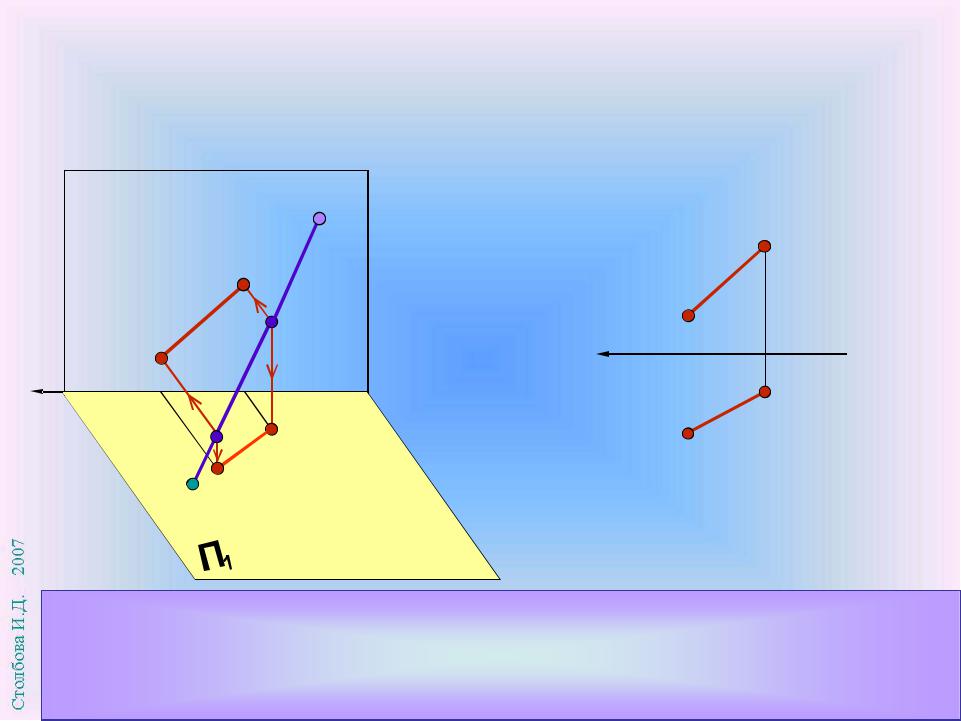
|
|
|
|
|
Следы |
прямой |
|
|||
Пространственная картина |
Комплексный чертеж |
|||||||||
|
|
|
|
|
|
АВ П |
|
|
|
|
|
П2 |
N |
|
|
|
|||||
|
АВ П1 |
|
|
В2 |
||||||
|
|
|
|
|
|
|
|
|||
|
|
В2 |
|
|
|
=М |
2 |
А2 |
|
|
|
|
|
|
|
=N |
|
|
|||
|
|
|
|
|
||||||
x |
А2 |
|
|
B |
|
|
x |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
|
A B1 |
|
|
|
|
B1 |
|||
|
|
|
|
А1 |
||||||
|
|
А1 |
|
|
|
|
|
|
||
|
M |
|
|
|
|
|
|
|||
След прямой – есть точка пересечения прямой с соответствующей плоскостью проекций. Точка М – это горизонтальный след прямой АВ , она имеет аппликату zМ = 0. Точка N – это фронтальный след прямой АВ, который имеет ординату yN = 0.
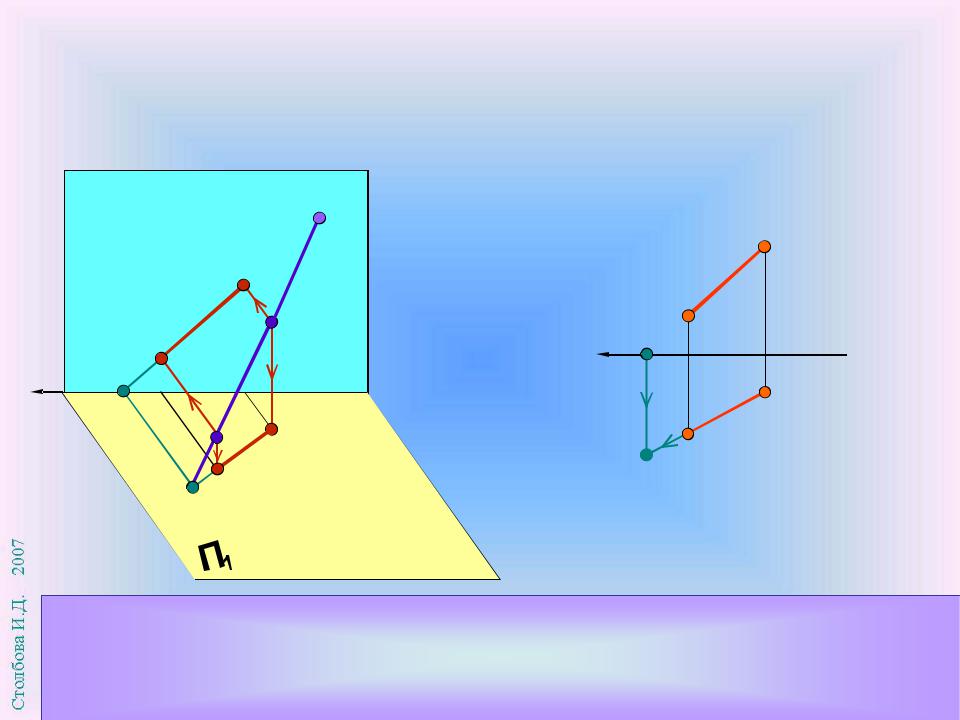
Следы прямой
Пространственная картина
П2 N
А2 |
В2 |
|
|
B |
||
|
||||||
x М2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
A B |
|||||
|
|
|
||||
|
|
|
А |
1 |
||
M M1 |
|
|||||
|
|
|
1 |
|
||
Комплексный чертеж
В2
А
М2 2
2
x
М1 А1 B1
Для построения горизонтального следа прямой АВ найдем на ней точку М с координатой z =0. Пересечение фронтальной проекции прямой А2 В2 с осью х определяет фронтальную проекцию следа M2 . Горизонтальная проекция следа М1 принадлежит горизонтальной проекции прямой
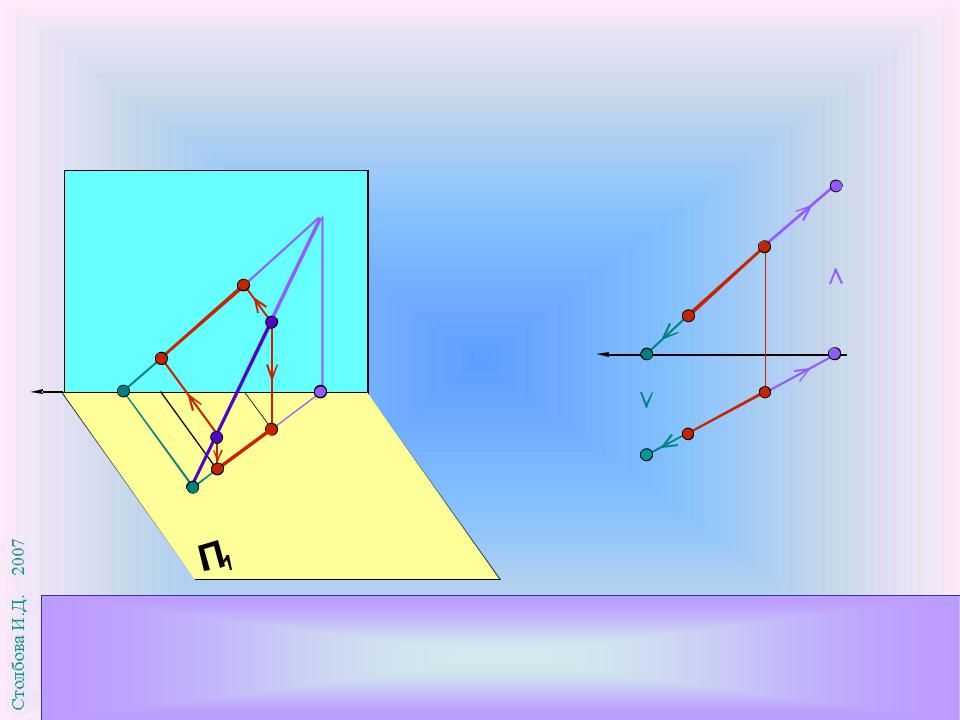
Следы прямой
Пространственная картина
П2 N2  N
N
|
|
В2 |
|
|
|
|
|
|
|||
|
А |
|
|
B |
|
x М2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
A B N1 |
||||
|
|
А |
1 |
||
|
M M1 |
|
|||
|
1 |
|
|||
Комплексный чертеж
|
|
|
|
В2 |
N2 |
||
|
|
А |
|
|
|||
М |
2 |
|
|
|
|||
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
x |
|
|
|
|
N1 |
||
|
|
|
|
B1 |
|||
|
|
А |
|||||
М |
|||||||
1 |
|
|
|
||||
1 |
|
|
|
|
|
||
Для построения фронтального следа прямой АВ найдем на ней точку N с координатой y = 0. Пересечение горизонтальной проекции прямой А1 В1 с осью х определяет горизонтальную проекцию следа N1 . Фронтальная проекция следа N2 принадлежит фронтальной проекции прямой
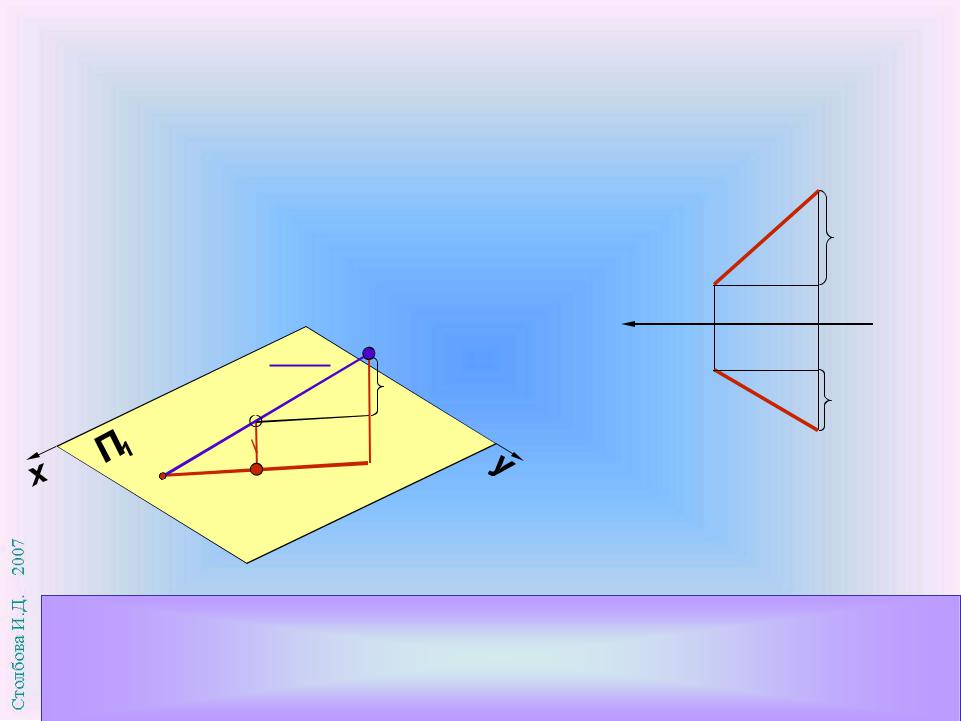
Определение характеристик отрезка
Метод прямоугольного треугольника
АВ 2 = x 2 + y 2 + z 2
x 2 + y 2 = А1 В1 2
н.в. B
A


 Кz
Кz
 А1
А1


 B1
B1
x
 В2
В2
z
А2 x
x
А1 x y
x y
 B1
B1
Длина проекции А1 В1 отрезка АВ есть гипотенуза прямоугольного треугольника с катетами x и y. Отрезок АВ – гипотенуза прямоугольного
треугольника АВК , один катет которого АК = А1 В1 , а другой равен разности расстояний z концов отрезка А и В от плоскости проекций П1
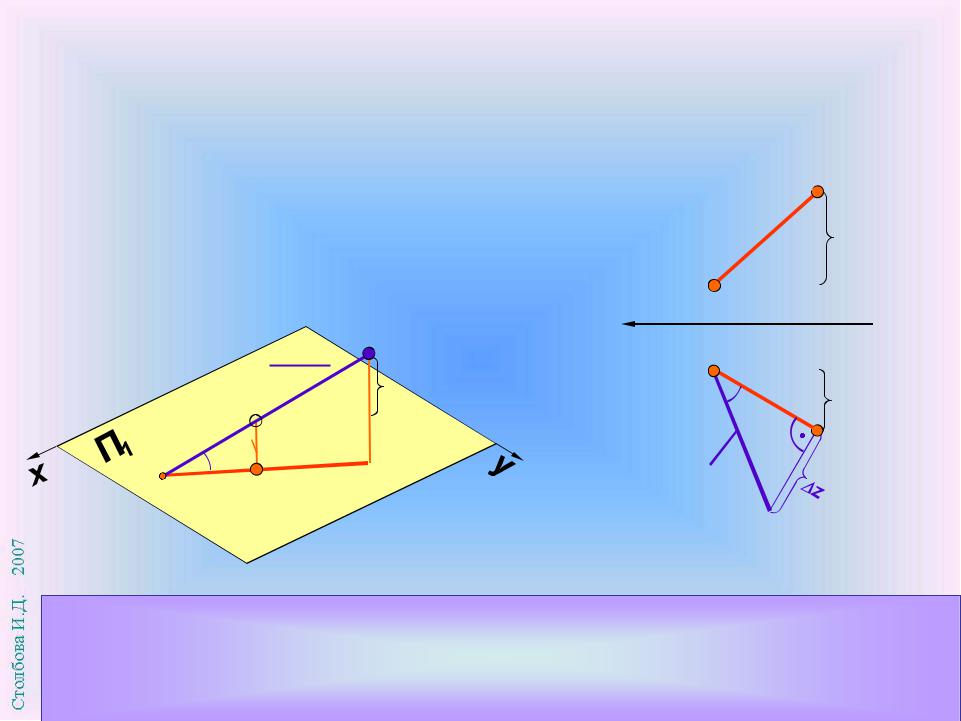
Определение характеристик отрезка
Метод прямоугольного треугольника
АВ 2 = x 2 + y 2 + z 2
x 2 + y 2 = А1 В1 2
н.в. B
A
 Кz
Кz
А1

 B1
B1
x
|
|
|
|
В2 |
|
|
|
|
|
|
|
|
|
z |
А |
|
x |
|
|
|
|
|
||
2 |
|
|
|
|
А |
|
x |
|
|
|
|
y |
||
1 |
|
|
B1 |
|
н.в |
. |
|
||
|
||||
|
|
|||
B0 
На горизонтальной проекции А1 В1 отрезка АВ построим прямоугольный треугольник А1 В1 В0 , второй катет которого равен z.
Гипотенуза А1 В0 треугольника равна натуральной величине отрезка АВ , а угол есть угол наклона отрезка АВ к горизонтальной плоскости
