Введение в комбинаторику и теорию вероятностей

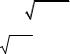
Proof

D(X ± C) = M (X ± C − M (X ± C))2 = = M (X ± C C − M (X ))2 = D(X ).

D(X ) = M (X − M (X ))2 = M (X 2 − 2 M (X ) X + (M (X ))2 ) = = M (X 2 ) − 2(M (X ))2 + (M (X ))2 = M (X 2 ) − (M (X ))2 .

From the 4-th property follows, that as D(X ) ≥ 0 , then M (X 2 ) ≥ (M (X ))2.

For an estimation of a deviation of possible values of an aleatory variable around its average value except the variance it is possible to use a medial quadratic deviation.

The medial quadratic deviation of an aleatory variable X terms a square root from a variance:

For example 6 σ(X ) = 1,89 ≈ 1,375.

3.3. CUMULATIVE DISTRIBUTION FUNCTION

OF AN ALEATORY VARIABLE. A DENSITY FUNCTION

OF A CONTINUOUS ALEATORY VARIABLE

As a cumulative distribution function of an aleatory variable X we can term function F(x) representing probability that the aleatory variable X in the result of an experiment will get a value, smaller than x, i.e.

713

Непрерывные случайные величины можно исследовать с помощью еще одной функции – плотности распределения вероятностей.

Плотность распределения вероятностей непрерывной случайной величины Х представляет собой первую производную от функции распределения и характеризует скорость изменения функции распределения этой случайной величины. Плот-

Можно выделить следующие основные свойства плотности распределения вероятностей непрерывной случайной величины:

1.f X (x) ≥ 0, так как функция распределения неубывающая функция.

2.FX (x) = x f X (x)dx.

−∞

3. P(a ≤ X ≤ b) = FX (b) − FX (a) = b f X (x)dx.

a

+∞

4. f X (x)dx = 1.

−∞

Числовые характеристики непрерывной случайной величины могут быть вычислены на основе плотности распределения вероятностей:

математическое ожидание

+∞

M (X ) = xfX (x)dx ;

−∞

дисперсия

+∞

D(X ) = (x − M (X ))2 fX (x)dx.

−∞

746

The continuous aleatory variables can be explored with the help of one more function – elementary probability law.

The elementary probability law of a continuous aleatory variable X represents the first derivative from a cumulative distribution function and characterizes a velocity of a modification of a cumulative distribution function of this aleatory variable.

It is possible to dedicate following basic properties of an elementary probability law of a continuous aleatory variable:

1. f X (x) ≥ 0 , because a cumulative distribution function — nondecreasing function.

2. FX (x) = x fX (x)dx .

− ∞

3.P(a ≤ X ≤ b) = FX (b) − FX (a) = b fX (x)dx.

a

+∞

4.fX (x)dx = 1.

− ∞

The numerical performances of a continuous aleatory variable can be computed on the basis of a density function:

Expectation:

+∞

M (X ) = xfX (x)dx .

−∞

Variance:

+∞

D(X ) = (x − M (X ))2 fX (x)dx .

−∞

75

При решении конкретных задач встречаются как дискретные, так и непрерывные случайные величины. В качестве примеров рассмотрим наиболее часто используемые распределения вероятностей: два дискретных (биномиальное и пуассоновское)

итри непрерывных распределения (равномерное, показательное

инормальное), распределения случайных величин.

3.4. ПРОСТЕЙШИЕ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН

Биномиальное распределение

К биномиальному распределению приводит следующая постановка. Производится n независимых повторных испытаний, в каждом из которых вероятность появления события равна p. Требуется найти вероятность того, что событие произойдет ровно k раз.

Закон распределения вероятностей дискретной случайной величины имеет вид (формула Бернулли)

Распределение Пуассона

К распределению Пуассона приводит следующая постановка. Найти вероятность того, что при большом числе повторных испытаний, в каждом из которых вероятность появления события очень мала и равна p (причем λ = n p < ∞ – конечно), событие произой-

дет ровно k раз. К пуассоновскому распределению приводят задачи, описывающие поведение некоторых процессов, например поток отказовсистемы, процессрегистрациичастицсчетчикомит.п.

768

At a solution of specific problems meet both discrete, and continuous aleatory variables. As examples we shall consider most frequently used probability distributions: two discrete (binomial and Poisson) and three continuous (uniform, exponential and normal distribution) distribution of aleatory variables.

3.4. THE ELEMENTARY DISTRIBUTION

OF ALEATORY VARIABLES

A binomial distribution

The following problem reduces in a binomial distribution. It is yielded n of independent retests, int each of them the probability of occurrence of event is peer p. It is required to find probability that the event will happen equally k of time.

The distribution of probabilities of a discrete aleatory variable look like (formula Bernoulli):

Expectation and variance are determined in the following way:

M (X ) = np. D(X ) = np(1− p).

Distribution of the Poisson

The following problem reduces in an distribution of the Poisson. Find the probability that at major number of retests, in each of which the probability of occurrence of event is very small and is peer n (and x1, x2, ..., xn – certainly), the event will happen equally k of time. In Poisson distribution reduce problems circumscribing behaviour of some processes, for example, stream of refusals of a system, process of filing of particles by the counter etc. Parameter of L represents intensity of such processes.

779

Параметр λ представляет собой интенсивность таких процессов.

Закон распределения вероятностей:

Математическое ожидание и дисперсия имеют вид

M (X ) = D(X ) = λ.

Равномерное распределение на [a, b]

Распределение вероятностей называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.

Плотность равномерного распределения имеет вид

Функция распределения равномерного распределения

7880

Expectation and variance look like

M (X ) = D(X ) = λ.

Uniform distribution on [a, b]

The probability distribution is termed as uniform, if on an interval, which posesses all possible values of an aleatory variable,

the density function maintains a constant value.

The denseness of a uniform distribution looks like:

Cumulative distribution function of a uniform distribution:

7981