Введение в комбинаторику и теорию вероятностей

Later on the concept of n factorial (n!) will be useful.

n factorial is the product of all natural numbers from 1 to n inclusive. ( n!=1 2 3 n ) Conditionally we will suggest that 0! = 1! = 1.

At this moment let us consider the standard enumerated problems.

An arbitrary k-element subset of an n-element set is called the combination of n elements taken by k. The order of elements is of no importance here. The number of combinations of n elements

Theorem. The number of combinations of n elements taken by k at a time is counted by the formula:

Proof.

Let A is n-element set. To construct k-element subset we must add one not belonging to this subset element of this set to (k – 1)- element subset. The number of such (k – 1)-element subsets equals

Cnk −1 and each of them can be turned into k-element subset in n – k + 1 ways. That is why the number of subsets is (n − k +1) Cnk −1 . But not all of them will be different, because

k-element subset can be constructed from (k – 1)-element subset in k ways by adding first element, the second one and so on to k-th one. As we have noted earlier, the order of elements is of no importance here, therefore the number we have calculated is greater by k times, than Cnk . That is why k Cnk = (n − k + 1)Cnk −1 .

213

Получили формулу (2.1).

Пример 5. В турнире принимали участие n шахматистов, и каждые 2 шахматиста встретились 1 раз. Сколько партий было сыграно в турнире?

Решение. Партий было сыграно столько, сколько можно выделить 2-элементных подмножеств в множестве из n элемен-

тов, т.е. C2 = n(n − 1) . n 1 2

Сочетания Cnk обладают многими интересными и важными свойствами. Рассмотрим некоторые из них.

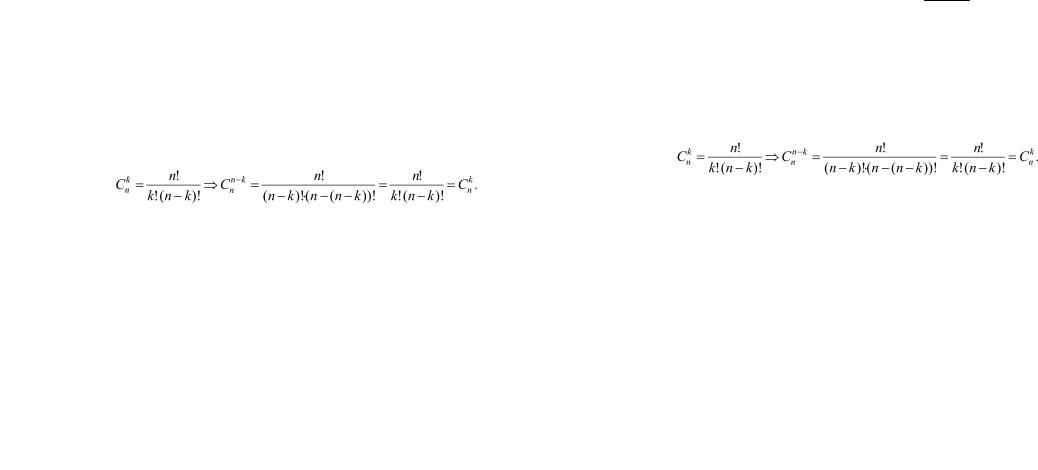
1. Cnk = Cnn− k .

Доказательство

224

= (n − k + 1)(n − k + 2) (n − 1)n . k(k − 1) 2 1

By this way we have obtained formula (2.1).

Example 5. There were n competitors in chess tournament. Every two players were to meet once. How many games were played?

Solution. The number of games equals the number of combi-

nations of n elements taken by 2 at a time: C2 = n(n − 1) . n 1 2

The binomial coefficient Cnk has many interesting and very

important properties for solution of combinatorial problems. Let us consider some of them:

1. Cnk = Cnn− k .

Proof

235

Последнее свойство позволяет описать процедуру последовательно получения числа сочетаний Cnk++11 при различных

значениях n и k.

Используя это свойство, можно представить число сочетаний в виде так называемого треугольника Паскаля:

C43 = C33 + C32 = 1+ 3 = 4;

…

Тогда треугольник Паскаля имеет вид

1

1 1

1 2 1

13 3 1

14 6 4 1

15 10 10 5 1

……………………..

Треугольник Паскаля обладает такими свойствами, когда каждый элемент строки, кроме крайних, равен сумме двух элементов, стоящих над ним в предыдущей строке. В начале и в конце каждой строки стоят 1.

Треугольник Паскаля, записанный с помощью сочетаний, выглядит так:

..................................

246

The last property gives us the possibility to describe the process of sequential obtaining the combinations Cnk at different mean-

ings of n and k.

Using this property it will be possible to imagine the combinations like the so called Pascal’s triangle.

C43 = C33 + C32 = 1+ 3 = 4; ….

Then Pascal’s triangle can be written in the following way

1

1 1

1 2 1

13 3 1

14 6 4 1

15 10 10 5 1

……………………..

Pascal’s triangle has the property: every element in one line except extreme ones equals the sum of two elements situated in the previous line above this element. At the beginning and the end of every line there are units.

Pascal’s triangle, which is written by using the combinations, looks like

C00

C10 C11

C20 C21 C22

C30 C31 C32 C33

..................................

257

Число сочетаний из n элементов по k с повторениями

представляет собой множество из k элементов, каждый из которых принадлежит одному из n типов (причем k может быть и больше n).

Эти множества отличаются от обычных сочетаний тем, что в них элемент может входить в различные сочетания разное число раз.

Число таких сочетаний с повторениями из n элементов по

~

k обозначается Cnk .

Докажем, что Cnk = Cnk+ k −1.

Доказательство. Каждое сочетание полностью определяется, если указать, сколько элементов каждого из n типов в него входит. Поставим в соответствие каждому сочетанию последовательность 0 и 1, составленную по правилу: напишем подряд столько 1, сколько элементов первого типа входит в сочетание, далее поставим 0, после него напишем столько 1, сколько элементов второго типа содержит это сочетание и т.д.

Таким образом, каждому сочетанию из n элементов по k

Cnn+−1k −1 = Cnk+ k −1 .

Пример 6. В оранжерее имеются цветы 10 наименований. Сколькими способами можно составить букет из 20 цветов?

Решение. В букет могут войти несколько цветов одного наименования, т.е. имеем сочетания с повторениями из 10

по 20 ( C~1020 ).

C~1020 = C2920 = C299 =10015005.

268

The number of recurrent combinations of n elements taken by k at a time are k-element sets and every element belongs to one of n types. (It being known that k can be greater than n).

The difference between these sets and usual combinations is that any element can belong to different combinations different number of times.

The number of recurrent combinations of n elements taken by

~

k at a time is denoted by Cnk . .

Let it be proved Cnk = Cnk+ k −1. .

Proof.

Every such combination is considered to be completely define, if we indicate, how many elements of every type are contained in it. We sholl set up the sequence of 0 and 1 in correspondence with every combination. This sequence will be made by using the following rule: we will write in succession as many 1 as elements of the first type are contained in the combination, then we shall set up 0, and after it, we will write as many 1 as elements of the second type are contained in this combination, and so on.

In this way, the sequence of k “1” and (n-1) “0” corresponds~to every combination of n elements taken k at a time. That’s why Cnk equals the number of the sequences of 1 and 0, i.e. Cnn+−1k −1 . According to the first property of Binomial coefficient we have Cnn+−1k −1 = Cnk+ k −1 .

Example 6. There are flowers of 10 names in a greenhouse. How many ways of making up a bouquets that consists of 20 flowers are there?

Solution. We can have some flowers with the same name in one bouquet. That is why we have the recurrent combinations of 10

elements taken by 20 at a time ( C~1020 ).

C1020 = C2920 = C299 = 10015005.

279

Множество, состоящее из n элементов, называется упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое натуральное число от 1 до n (номер элемента) таким образом, что различным элементам соответствуют различные числа. Всякое конечное множество можно сделать упорядоченным.

Число различных способов, которыми может быть упорядочено данное множество, состоящее из n элементов, называется числом перестановок множества и обозначается Pn .

Теорема. Число перестановок из n элементов по k вычисляется следующим образом:

Доказательство. Будем последовательно выбирать элементы данного множества и размещать их в определенном порядке на n местах. На первое место можно поместить любой из n элементов, на второе любой из оставшихся, т.е. (n −1) эле-

ментов и т.д.

Поправилупроизведенияполучим Pn = n (n −1) 2 1= n!

Получили формулу (2.2).

Пример 7. Сколько можно составить перестановок из n элементов, в которых данные два элемента не стоят рядом?

Решение. Определим число перестановок, в которых данные элементы (для определенности a и b) стоят рядом: a на первом месте, b на втором, a на втором, b на третьем, …, a на (n – 1)-м месте, b на n-м – таких случаев (n – 1). Однако впереди можно ставить b, а затем a – таких случаев также (n – 1), т.е. существует 2 (n – 1) случая, когда a и b стоят рядом. Каждому из этих случаев соответствует (n − 2)! перестановок. Используя

правило умножения, искомое решение можно записать в виде

P = n!− 2(n − 1)(n − 2)!= (n − 1)!·(n − 2).

2830

n-element set is called ordered, if every element of this set corresponds to natural numbers from 1 to n. It being known that different elements correspond to different natural numbers. It will be good here to note that every finite set may be ordered.

The number of different ways where n-element set can be odered is called permutations and is denoted by Pn.

Theorem. The number of permutations of n elements is calculated by the formula:

Proof.

We will sequentially choose all the elements of the given set and arrange them on n places. We can put each of n elements on the first place, each of (n-1) elements on the second place and so on. According to the rule of product we have:

Pn = n(n −1) 2 1= n!

Example 7. How many possible combinations of n elements where two given elements do not stay near each other can we construct?

Solution. To solve this problem at first we shall find the number of permutations where two given elements (for example, the element ‘a’ and the element ‘b’) stay near each other: the element ‘a’ can stay on the first place and the element ‘b’-on the second one; the element ‘a’ can stay on the second place and the element ‘b’-on the third one;...; the element ‘a’ can stay on the (n – 1)th place and the element ‘b’-on the nth one. The number of such cases is (n – 1). But in this problem another situation is possible, when the element ‘b’ is in front of the element ‘a’. And the number of them is the same. That is why we have 2*( n – 1) cases, when the element ’a’ and the element ‘b’ stay near each other. Each of these situations corresponds to (n − 2)! permutations. Using the rule of product, we have

P = n!− 2(n − 1)(n − 2)! = (n − 1)!·(n − 2).

2931

Число упорядоченных k-элементных подмножеств множества из n элементов называется числом размещений из n

элементов по k и обозначается Ank .

Теорема. Число размещений из n элементов по k вычисляется следующим образом:

Доказательство. Исходное множество из n элементов – неупорядоченное, поэтому каждое его подмножество может быть упорядочено каким-либо возможным способом. Число всех k-элементных подмножеств исходного множества из n элементов

равно Cnk . Каждое такое подмножество можно упорядочить k! способами (число перестановок из k элементов). Тогда

Получили формулу (2.3).

Пример 8. Учащемуся необходимо сдать 4 экзамена за 8 дней. Сколькими способами это можно сделать?

Решение. Искомое число способов равно числу 4-эле- ментных упорядоченных подмножеств из 8 элементов, т.е.

A84 = 8 7 6 5 = 1680 способов. Если известно, что последний экзамен будет сдаваться на восьмой день, то число способов равно 4 A84 = 7 6 5 4 = 840.

Назовем размещениями с повторениями из n элементов по k число всевозможных упорядоченных k-элементных подмножеств множества n различных элементов, различающихся самими элементами или их порядком или количеством повторяющихся элементов (k может быть и больше n).

302