Введение в комбинаторику и теорию вероятностей

Классическое определение вероятности

Пусть осуществляется n исходов (элементарных событий), удовлетворяющих следующим условиям:

♦число исходов n – конечно;

♦один из исходов ω1, ω2 , ..., ωn обязательно произойдет;

♦два исхода одновременно произойти не могут;

♦все исходы равновозможные.

Такое множество исходов называется пространством элементарных событий.

Пусть пространство элементарных исходов состоит из n исходов, и событию A благоприятствует m исходов из них, тогда вероятность события A определяется следующим образом:

Пример 1. Найти вероятность того, что при случайной сдаче 6 карт из 36 будет сдано 3 туза.

Решение. Общее количество сдач представляет собой все возможные 6-элементные подмножества множества из 36 эле-

ментов, т.е. n = C366 . Всего в колоде 4 туза, поэтому число возможных вариантов, при которых в сдаче окажется 3 туза, равно C43 . Каждой такой сдаче соответствует один из C323 вариантов

(без тузов в колоде 32 карты, необходимо из них взять еще 3, чтобы в сдаче оказалось 6 карт). Согласно правилу умножения

Пусть Ω = (ω1 ,ω2 ,...,ωn ) – пространство элементарных событий с конечным числом исходов (n < ∞).

С учетом введенных выше определений событием бу-

дем называть всякое подмножество множества Ω . Будем обозначать события большими буквами латинского алфави-

та (A, B,C,...Z Ω).

42

The classical definition of probability

Assume, there are n outcomes fulfil to the next conditions:

♦outcomes quantity n – is finite;

♦one of the outcomes ω1, ω2, …, ωn mandatory occur;

♦two outcomes can not occur in the same time;

♦all outcomes are equally likely

Such a set of outcomes is called sample space.

Assume the sample space consists of n outcomes. And for some event A is favor m outcomes of them, therefore probability of event A defined by the following way:

Example 1. What is the probability that 6 cards of 36 dealt at random will be given 3 aces.

Solution

The general quantity of dealing represents all-possible 6- elements subsets of a set consisting of 36 elements, i.e. n = C366 . The standard deck has 4 aces, therefore the quantity of possible variants when dealing will consist of 3 aces is C43 . Every such deal corresponds to the one of C323 variants. According to the rule of product

Let Ω = (ω1,ω2 ,...,ωn ) – sample space with finite quantity of outcomes (n < ∞).

With help of definitions given above, the event is any subset

of set Ω . We shall denote events with the big Latin letters (A, B,C,...Z Ω).

435

Обозначим вероятность каждого элементарного события ωi через pi ( p(ωi ) = pi ,i = 1, ...,n) . Эти вероятности должны удовлетворять следующимусловиям:

( p(ωi ) ≥ 0,i = 1,...,n) ;

n

p(ωi ) = 1 .

i=1

Вероятность события A = (ω1 ,ω2 ,...,ωk ) может быть опре-

делена через вероятности элементарных событий следующим образом:

в формулу (3.1).

Определим простейшие операции над событиями.

1.Сумма двух событий A и B представляет собой событие, состоящее в том, что произойдет хотя бы одно из событий A или B (по существу, имеет место объединение этих событий

( A B )).

2.Произведение двух событий A и B представляет собой событие, состоящее в том, что произойдут одновременно события A и B (по существу, имеет место пересечение этих событий

( A ∩ B )).

3.Событие не A ( A ) называется противоположным к событию A, если оно состоит в том, что событие A не произошло. При этом верно:

♦A A = Ω ,

♦A ∩ A = ,

где Ω – пространство элементарных событий; – пустое множество.

446

To each simple event ωi (i = 1, .., n) we assign a real number, denoted by pi ( p(ωi ) = pi ,i = 1, ...,n) that is called the probability of the event ωi . These numbers can be assigned in an arbitrary manner as long as the following two conditions are satisfied:

( p(ωi ) ≥ 0,i = 1,...,n) ;

i=1

If p(ωi ) = 1 , i = 1,...,k (that is events ωi – are equally likely), k

so rule (3.2) leads to the rule (3.1).

Union, Intersection and Complement of Events

1.In general, if A and B are two events in a sample space, the event A or B is defined to be the union of A and B ( A B ).

2.The event A and B is defined to be the intersection of A and

B ( A ∩ B ).

3.The event not A ( A ) is defined to be contrary (mutually exclusive) to the event A if event A is impossible (not occur). In this case right the following

♦A A = Ω ,

♦A ∩ A = ,

where Ω is sample space, – empty space.

457

Ω представляет собой достоверное событие.представляет собой невозможное событие.

События A и B называются несовместимыми, если они в условиях одного и того же опыта одновременно произойти не могут, но принадлежат одному и тому же пространству элементарных событий, т.е. A B = .

События A1, A2 ,..., Ak образуют полную группу событий,

если в результате опыта хотя бы одно из них произойдет. При этом должны быть удовлетворены следующие два условия:

♦Ai = Ω ,

i=1k

противоположными событиями.

Рассмотрим основные вероятностные соотношения, которые вытекают из формул (3.1) и (3.2).

1.p(Ω) = 1 – вероятность достоверного события равна 1.

2.p( ) = 0 – вероятность невозможного события равна 0.

3.Для любого случайного события A справедливо соотношение

0≤ p(A) ≤ 1.

4.Теорема сложения вероятностей для несовместимых событий A и B (исходя из определения несовместимых событий) имеет вид

5. Дляпротивоположныхсобытийсправедливосоотношение

6. Формулу (3.3) можно обобщить на конечное число несовместимых событий:

468

Ωcertain event.

impossible event.

Events A and B are called exclusive events if the event “A and B” is impossible, that is A B = .

Events A1, A2 ,..., Ak form a complete group of events, if they

cannot occur as a result of the same experiment, but they belong to the same sample space. At this rate the following condition is correct:

We shall to examine the main probability correlation that followed from the rules (3.1) and (3.2).

1.p(Ω) = 1– probability of reliable event is 1.

2.p( ) = 0– probability of impossible event is 0.

3.For any random event A is correct the formula

0≤ p(A) ≤ 1.

4.Addition theorem of probabilities for exclusive events A and B (according to the definition of them) is given by:

6. Rule (3.3) can be generalized for finite quantity of sample events

479

i=1

7. Если события H1, H2 ,..., Hk образуют полную группу событий, то

i=1

8.Для произвольных событий A и B можно записать

10. Если A B , то p(A) ≤ p(B).

Важными в теории вероятностей являются понятия зависимых и независимых событий.

Событие А называется независимым от события В, если вероятность события А не меняется от того, произошло событие В или нет, в противном случае событие А называется зависимым от события В. Характеристики зависимости–независимости двух событий являются взаимными.

При решении вероятностных задач, которые допускают геометрическую интерпретацию, удобно пользоваться понятием

геометрическая вероятность:

где μ – это мера, представляющая собой длину (L), площадь (S) или объем (V).

4850

i=1

7. If events H1, H2 ,..., Hk form complete group of events, so

10. If A B, then p(A) ≤ p(B).

In the theory of probability definitions of dependent and independent events are very important.

We often encounter events A and B which are independent, in the sense that neither one affects the probability of the other. This means that probability of B is not changed by the information that A has occurred, and vice-versa. If not, event A is dependent from event B.

At the process of solving probabilistic problems, which assume geometrical interpretation, geometrical probability is very

where μ – is the measure of geometrical object (length (L), square (S) or volume (V)).

4951

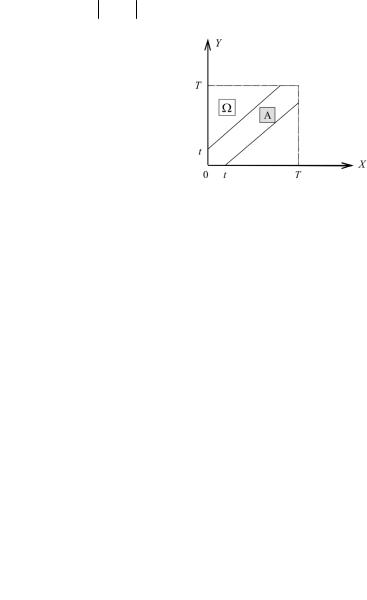
Пример 2. В городе Осторожность дуэли редко кончались трагически. Каждый из дуэлянтов являлся в случайный момент времени от 5 до 6 часов утра и 5 минут ждал. Какова вероятность того, что дуэль состоится?

Решение. Пусть Х – время прихода первого дуэлянта, Y – время прихода второго ( 0 ≤ X ,Y ≤ T ). Тогда Ω :[0,T ] [0,T ] ;

A : X − Y ≤ t, где T – 1 час; t – 1/12 часа (5 минут).

Докажем формулу (3.11) исходя из классического определения вероятностей.

502