Шестак Вакуумная техника. Концепция разреженного газа 2012

В настоящее время моль определяется так: это количество вещества, содержащего столько же структурных элементов (атомов, молекул, ионов или других частиц), сколько их содержится в 0,012 кг углерода-12.

Моль – одна из семи основных единиц международной системы единиц СИ.

На основании закона Авогадро определено число Лошмидта NL= 2,69 · 1019 мол · см–3. Очевидно,

что NL = NА /Vμ .

Число Лошмидта, соответствующее атмосферному давлению 105 Па, удобно использовать при оценке достигнутого в вакуумной системе разрежения х, составляя простое соотношение:

105 Па – 2,69 · 1019 мол · см–3; 10–3 Па – х, мол · см–3,

получаем х = 2,69 · 1011 мол · см–3.

Постоянные Авогадро и Лошмидта настолько велики, что с трудом поддаются воображению.

Например:

•если вылить стакан воды в море и подождать, пока вода из стакана равномерно рас-

пределится по всем морям и океанам, до самого их дна, то, зачерпнув воду тем же стаканом в любом месте Мирового океана, объем которого более 1400 млн км3, окажется, что в него обязательно попадет несколько десятков молекул воды, из тех которые были когда-то в стакане;

•если взять «NА банкнот», то они покроют все материки и острова (площадь суши на Земле – 149,1 млн км2) 2-километровым плотным слоем…

6.Уравнение состояния газа. Для идеального газа, молекулы которого ведут себя в столкновениях подобно абсолютно упругим шарам с диаметром, равным эффективному диаметру молекул

~5 · 10–9 м, уравнение состояния газа (термическое уравнение), полученное Клапейроном в 1865 г. для ограниченного количества газа, может быть записано как: pV/T = В, где величина В зависит от массы газа.

Дмитрий Иванович Менделеев

(1834 – 1907)

великий русский ученый, стоящий в российском сознании вторым в ряду наших великих ученых после М.В. Ломоносова

(см. подробнее сайт: http://glazev.rossija.info/viewtopic.php?t=2774)

(слева – портрет кисти И. Е. Репина, 1885)

В 1874 году Д.И. Менделеев нашёл общее уравнение состояния идеального газа, включающее как частность законы Бойля–Мариотта, Шарля, Гей-Люссака, Авогадро и уравнение Клапейрона. Открытие Менделеева систематизировало разрозненные факты, правила и законы, составляющие теорию газа, и красиво завершило формирование МКТ газа.

С момента открытия Менделеева уравнение состояния газа для одного моля газа в МКТ обычно записывается в виде уравнения Менделеева–Клапейрона:

где pVμ – количество газа в моле; p – давление, Па; Vμ – молярный объем газа, при нормальных условиях (Т ≈ 273 К, р ≈ 105 Па) молярный объем Vμ = V/(M/μ), где M – масса газа, μ – молярная масса га-

за, M/μ – число молей в объеме V, м3; R – универсальная газовая постоянная, R = kNА ≈ 8,314 Дж · моль–1 · К–1, T – температура, К; k – постоянная Больцмана, k =1,38 · 10–23 Дж · К–1.

41

где F – сила взаимодействия молекулы и стенки, τ – время удара.

Путь, который молекула проходит от одного удара о стенку до другого, равен хорде АВ, то есть величине 2R сos φ46. Найдем число ударов молекулы о стенку за одну секунду f*. Оно равно отношению скорости молекулы vi к величине пути, проходимого молекулой от одного удара до другого: f* = = vi /2R сosφ. Тогда величина импульса, сообщенного стенке, например, за секунду, будет равна

2mivi сosφ vi/2R сosφ = miv2i /R, а сумма импульсов всех N молекул за секунду (суммарная сила) F =

= 1/R ∑ miv2i.

Разделив силу на площадь сферы A = 4πR2, найдем давление газа р, оказываемое им на стенку камеры, исходя из того, что все N молекул ведут себя в объеме аналогично:

р = F/A = 1/ R ∑ miv2i/4π R2 = 1/3∑ miv2i /V, где V = 4/3 π R3.

Можно записать рV = 1/3∑ mi v2i = 2/3 ∑ mi v2i /2 = 2/3 ∑Еi , где Еi = miv2i /2 кинетическая энергия одной молекулы.

Умножив и разделив правую часть полученного выражения на число молекул в объеме N, получим рV = 1/3 mN ∑ v2i /N; выражение (Σvi2 N ) можно заменить на некую среднеквадратичную ско-

рость молекул в объеме ‹v›кв., тогда основное уравнение молекулярно-кинетической теории запи-

сывается так:

Исходя из того, что уравнение состояния идеального газа pV = NkT, можно определить значение среднеквадратичной скорости молекул

Расчеты по этой формуле при Т = 293 К дают для молекулярных: водорода ‹v›кв = 1755 м/с, азота – 493 м/с, кислорода – 440 м/с и т.д.

Основное уравнение молекулярно-кинетической теории в явном виде представляет количество газа при известной температуре как количество энергии в джоулях, Дж.

Отсюда следует ряд интереснейших выводов, которые позволяют дополнить аппарат анализа МКТ газа аппаратом анализа, развитым в термодинамике, например:

1)под универсальной газовой постоянной можно понимать величину энергии, содержащейся в моле при заданной температуре, и эта энергия одинакова для всех газов;

2)можно интерпретировать давление находящегося в отсеченном объеме газа и имеющего размерность [Па] = ML–1T–2, как энергетическую концентрацию в этом объеме ML–1T–2 = MT–2 L2 L–3 с размерностью Дж · м–3 и тогда представление количества газа pV в джоулях является более естественным для количества остаточного газа, находящегося при заданной температуре Т в ограниченном объеме V, так как в этом случае можно говорить о внутренней энергии термодинамической системы – ансамбля молекул остаточного газа, не обсуждая характер взаимодействия отдельных молекул между собой и со стенками (вариант описания А, см. рис. 1.1.6).

Тогда, если рассматривать удаление количества газа d(pV) в единицу времени dt как образование

потока откачки Qоткачки, то размерность этого потока выражается в ваттах:

1.1.3. Шкала плотности веществ. Давление газа. Движение молекул в газе. Длина свободного пробега молекул. Критерий Кнудсена. Разрежение газа

Шкала плотности разработана по аналогии с широко известной шкалой электромагнитных колебаний, диапазон которых в длинах волн, простирается от 105 (низкочастотные колебания и радиоволны) до 10–11 м (ядерное γ-излучение). Подобные шкалы позволяют позиционировать не только отрасли наук, занимающихся исследованиями в определенных поддиапазонах шкалы (для электромагнит-

46 Рассмотрение подобного движения молекулы по хорде АВ справедливо для разреженного газа (вакуума); взаимодействие с поверхностью в точке А, конечно, принято чисто условно, в молекулярной физике отражение происходит не под углом падения!

43

ных колебаний известны шесть отдельных областей излучений, отличающихся и методикой исследований, и теоретическим обеспечением, и техническими средствами, например от мобильных телефонов до адронного коллайдера), но и классифицировать используемые методы исследований и технические средства47.

Шкала электромагнитного излучения. По горизонтальным осям отложены: вверху – частота колебаний f в герцах, внизу – длина волны λ в метрах

Плотность веществ обычно представляется в единицах массовой плотности ρ = dm/dV, где dm – масса вещества (кг) в элементе объема dV, м3; для вакуумной техники она может быть представлена, например, в единицах молекулярной концентрации n, мол/м3, определяемой как n = N/V, где – N, количество молекул (мол) в объеме V, м3.

Диапазон известных массовых плотностей простирается от 1017 кг/м3 в ядерной физике (плотность ядерного вещества) до 10–23 кг/м3 в межзвездном космосе, а диапазон, в котором получают и используют технический вакуум, покрывает 17 порядков, что сравнимо с диапазоном генерируемых и используемых электромагнитных колебаний.

Шкала плотности для известных агрегатных состояний веществ приведена в табл. 1.1.1.

Если рассматривать вещество как среду, в которой проводится эксперимент, то возникает необходимость, кроме характеристики «плотность» (массовая или молекулярной концентрации), учитывать энергетическую характеристику газа, параметрами которой являются температура вещества T и давление p. Повторим, что широко используемое в теории газа понятие «давление» соответствует идеальной модели, в которой соударения молекул между собой и со стенками вакуумной камеры абсолютно упруги.

Интерес к давлению газа (особенно к атмосферному) не был праздным, так как давление (или перепад давлений), преобразованное в силу, может быть использовано для производства внешней работы, например, для подъема воды48.

Молекулярно-кинетическая теория газа базируется именно на использовании параметра «давление». Исторически именно давление определило интерес к вакууму, как к среде, в которой «нет» давления, а есть «пустота».

Уже в эпоху эллинизма (330 – 27 гг. до н.э.) создавались различные водяные насосы, действие которых основано на создании разрежения воздуха под поршнем. До нас дошел рисунок пожарного насоса, изобретенного александрийским ученым Ктесибием49. Водяной насос был по существу прообразом вакуумного поршневого насоса.

47Шестак В.П. Основы физических измерений. Гносеологические аспекты. Москва – Томск: Изд-во ТГПУ, 2004. С. 21 – 23.

48См., например, очень интересное эссе: Борисов В.П. Изобретение вакуумного насоса и крушение догмы

«Боязни Пустоты». URL: http://innovatory.narod.ru/borisov.html.

49Ктесибий (около 150 г. до н. э.), древнегреческий механик-изобретатель из Александрии. Изобрел двухцилиндровый поршневой пожарный насос, снабженный всасывающими и нагнетательными клапанами, воздушным уравнительным колпаком и рычагом-балансиром для ручного привода. Насос имел все основные детали

44

Но на шаг от водяного насоса Ктесибия к водяному вакуумному насосу Герике потребовались почти два тысячелетия, так как «пустота» стала предметом церковных догм и запретной темой!

После «мрака средневековья с блеском придворной культуры, кострами инквизиции и устремленной к небесам тамплиерской готикой» 74-летний Галилей в своей последней книге «Беседы и математические доказательства двух новых наук»», вышедшей в 1638 г., бросая вызов инквизиции, рассуждал об ограниченности «силы боязни пустоты».

современных ручных пожарных насосов. Сведения о Ктесибии сохранились в трудах Герона и римского архитектора Витрувия.

50 Афанасий Кирхер (1602 – I680) – авторитетный немецкий ученый тех лет, занимавшийся естественными науками, лингвистикой, древностями, теологией, математикой. Был профессором нескольких университетов, занимался физикой и техникой, особенно оптикой (в частности, он изобрел так называемый волшебный фонарь).

45

Возникшую в то время в обществе борьбу по вопросу «пустоты» блестяще использовал бургомистр г. Магдебурга Отто фон Герике – богатый и знатный человек51, который был блестящим естествоиспытателем. Вместо того чтобы погрязнуть в дискуссиях с коллегами, он принял очень остроумное решение и остался в памяти человечества на века своим экстравагантным экспериментом по «борьбе лошадей с атмосферным давлением», в котором использовались два медных полушария около 14 дюймов (35,5 см) в диаметре, полые внутри и прижатые друг к другу. Из собранной сферы выкачивался воздух, и полушария удерживались вместе только давлением внешней атмосферы.

Панорама Регенсбурга, каменный мост через Дунай (построен в период 1135–1146 гг.)

Фон Герике в качестве PR-акции в 1654 г. продемонстрировал эксперимент рейхстагу52 в присутствии императора Фердинанда III53. После выкачивания из сферы воздуха, 16 лошадей54 (по восемь с каждой стороны) не смогли оторвать полушария друг от друга.

В результате Отто фон Герике не только наглядно доказал неверующим возможность технического получения «пустоты» и существование давления воздуха, но и получил от императора деньги для занятия наукой. Герике впоследствии установил упругость и весомость воздуха, его способность поддерживать горение и дыхание, проводить звук. Доказал наличие в воздухе паров воды. В 1660 г. Герике построил первый в мире водяной барометр и использовал его для предсказания погоды. Занимаясь астрономией, он высказал мнение о том, что кометы могут возвращаться. В 1663 г. Герике создал одну из первых электрических машин – вращающийся шар из серы, натираемый руками, и обнаружил явление электростатического отталкивания однополярно заряженных предметов. В 1672 г. году он открыл, что заряженный шар потрескивает и светится в темноте (электролюминесценция). В этом же году он опубликовал результаты своих исследований в сочинении «Новые, так называемые магдебургские, опыты о пустом пространстве».

Движение молекул в газе. Длина свободного пробега молекул. Критерий Кнудсена

Название «газ», введенное примерно в 1610 г. голландцем Ван Гельмонтом, происходит от греческого слова «haos» и хорошо отражает истинный характер движения частиц в газе, отличающийся полной беспорядочностью, хаотичностью. В отличие, например, от жидкости газы не образуют свободной поверхности и, непрерывно двигаясь, равномерно (равновесно) заполняют весь доступный им объем.

Каждая молекула движется вдоль прямой линии до очередного столкновения с другой молекулой (см. рис. 1.1.3,а) или со стенкой объема (вакуумной камеры) (см. рис. 1.1.3,б).

В идеальном газе порядок величины среднего расстояния ‹r› между молекулами можно определить как ‹r› ≈ n–1/3, где n – число частиц в единице объема или плотность газа.

Если пользоваться моделью взаимодействия частиц газа, в которой молекулы представляются твердыми упругими шариками диаметром dм, то условие идеальности газа записывается как n · dм 3 << << 1. Характерный размер молекул газа можно в среднем оценить как dм = 3 · 10–10 м. Это означает, что газ является идеальным, если n << 3 · 1022 мол · см–3. Такому условию заведомо отвечает любой газ (например, воздух), находящийся при нормальных условиях (давление p = 105 Па, молекулярная плотность 2,69 · 1019 мол · см–3, температура T = 273 K).

51В сочетании с фамилией приставка «фон» в немецком языке означает дворянский титул.

52Рейхстаг (der Reichstag) – верховный законодательный орган власти и центральный элемент всей консти- туционно-правовой системы Священной Римской империи, высший сословно-представительный орган, представляющий интересы политической элиты империи с законодательными и судебными функциями, до падения империи в 1806 г. заседал в Регенсбурге.

53Фердинанд III в 1636 г. был избран римско-германским королем именно в Регенсбурге.

541 лошадиная сила ≈ 740 Н · м/с = 740 Вт.

46

Длина свободного пробега молекул ‹λ›

Предположим, что все молекулы имеют диаметр dм = 2a0 ≈ 1 Å (a0 – первый радиус Бора), тогда эффективное сечение столкновения55 для разреженного газа

σ ≈ πdм2 = 3,1 · 10–16 см2

(для атмосферного воздуха при нормальных условиях с учетом парного потенциала взаимодействия молекул56 почти на два порядка больше, хотя также ничтожно σ =10–14 см2).

Эффективное сечение столкновения, по сути, является вероятностью взаимодействия движущейся молекулы с другими молекулами.

Допустим, что все молекулы, кроме одной, покоятся. Движущаяся со скоростью v молекула будет сталкиваться (точнее, взаимодействовать) со всеми молекулами, центры которых лежат на расстоянии, меньшем или равном dм от прямой, вдоль которой она движется (рис. 1.1.9).

За время dt молекула проходит расстояние λ = v·dt, и «прочеркивает» объем σλ. Среднее число молекул в этом объеме или, что то же самое, среднее число столкновений за время dt составит

и 2 относятся к двум сталкивающимся молекулам и

vср. рез = 2vкв2 в. при условии, что v12 = v22 = 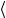vкв2 . Тогда средняя длина свободного пробега молекулы

Для воздуха при 293 К принимается57 <λ>, м = = 6,51 · 10–3/р, где размерность давления р в Па.

Рис. 1.1.9. Модель столкновения молекул

Критерий Кнудсена

Длина свободного пробега, с одной стороны, определяется разрежением, достигнутым в газе, а с другой, входя в выражение, представляющее собой критерий Кнудсена (Kn), Kn = λ /dэф, где dэф – характерный геометрический параметр задачи (принято говорить об эффективном размере системы, но такой термин ничего не объясняет, так как он зависит от цели создания вакуумной системы), в которой участвуют молекулы, является своеобразным «индикатором степени вакуума» в системе.

Критерий Кнудсена назван в честь датского физика Мартина Кнудсена и имеет, как было сказано выше, важное значение в вакуумной технике, поскольку численная величина Kn характеризует степень разреженности газа или степень достигнутого технического вакуума.

Если Kn << 1 (теоретически при 0), справедливо основное предположение о сплошности (континуальности) среды и отсутствии вакуума. МКТ достаточно полно описывает газ в этом состоянии.

55Эффективное сечение – мера вероятности столкновения микрообъектов (атомов, ядер и частиц) в виде

эффективной площади их поперечного сечения. Это основная величина, характеризующая вероятности столкновений (реакций) в микромире. Эффективное сечение измеряют в барнах (б); 1 б = 10–24 см2.

56Понятие парного потенциала подразумевает, что взаимодействие двух частиц зависит только от их взаимного расположения и не зависит от положения каких-либо других частиц.

57Вакуумная техника: Справочник /К.Е. Демихов, Ю.В. Панфилов, Н.К. Никулин и др.; под общ. ред. К.Е. Демихова, Ю.В. Панфилова. 3-е изд., перераб. и доп. М.: Машиностроение, 2009. С. 43.

47

Если Kn >> 1 (теоретически при ∞), движение молекул можно рассчитывать, не рассматривая столкновений молекул между собой, – свободное молекулярное течение. В этом случае можно смело сказать, что единой теории разреженного газа не существует, а модели, принятые за основу в мо- лекулярно-кинетической теории, не работают.

Длина свободного пробега обратно пропорциональна молекулярной концентрации в объеме, что в полулогарифмическом масштабе λ от lg n представляется обратной линейной зависимостью. Линейная зависимость переходит в постоянную величину при

λ = dэф (рис. 1.1.10).

В ряде случаев, например в напылительных установках, длина свободного пробега молекул может являться самостоятельной характеристикой вакуумной системы.

Длина свободного пробега как параметр, характеризующий разреженный газ, имеет важное значение при описании явлений молекулярного переноса – диффузии, внутреннего трения и теплопроводности в области низкого вакуума, так как перенос осуществляется от слоя к слою, а толщина слоев равна λ .

Средняя длина свободного пробега электронов λe в газе, в котором средняя длина свободного пробега молекул равнаλ , вычисляется по формуле

λe ~ 5,6 λ .

Разрежение газа

Шкала плотности веществ, приведенная в табл. 1.1, использует параметр «молекулярная концентрация» n – отношение количества молекул в объеме V к величине этого объема, что не всегда справедливо, поскольку молекулы могут находиться как в ограниченном объеме, так и в открытом пространстве. В последнем случае в пространстве выделяется гипотетический объем dV и рассматриваются находящиеся в нем dN молекул. В этом случае говорят о параметре «локальная молекулярная концентрация», который еще не стал общепринятым в вакуумной технике в связи с тем, что не существует практики ее измерения58.

Можно ввести новый параметр – «параметр разрежения» Di, который рассматривается как гипотетическое59 расстояние между свободными молекулами газа. Очевидно, что при высоком разрежении длина свободного пробега будет велика и в пределе, как показано на рис. 1.1.10, достигнет практического для ограничивающей системы максимума, определяемого параметром Кнудсена dэф.

Если считать разрежение равным величине среднего расстояния между молекулами ‹r›, можно записать Di ≈ n–1/3, м.

Вакуумная техника и технология – средства и способы, обеспечивающие разрежение газа и последующую работу либо с ним, либо в нем

Параметр разрежения Di не учитывает условия замкнутости и величины объема, как, например, критерий Кнудсена, и ранжирует получаемые в газе разрежения аналогично молекулярной концентрации60. Это позволяет построить шкалу, единую для газов, жидкостей и твердого тела. Подобная шкала приведена на рис. 1.1.11.

58Шестак В.П. АС 1302156 СССР, МКИ G01L 21/00. Способ измерения (локального) давления. Заявлено

13.06.1985. Опубл. 07.04.1987. Бюл. № 13. 2 с.: ил.

59Гипотетический – не существующий в реальности или ненаблюдаемый, но смоделированный на основании косвенных данных.

60В том числе по уровню достигаемого вакуума.

48

1.1.4. Функция распределения. Скорости молекул. Распределение Максвелла. Средняя скорость свободных молекул

Функция распределения

При полном описании ансамбля молекул необходимо решать систему N уравнений, описывающих движение каждой молекулы:

ствующая на i-ю молекулу, i = 1, 2, 3,..., N (N – число молекул в системе), например в зоне А

(рис. 1.1.12).

Для решения системы уравнений необходимо знать начальные координаты молекул, начальные скоростиG и принять какую-либо модель взаимодействия молекул с внешней средой для определения

сил F , действующих на молекулу в зоне А. Такой моделью, справедливой для вакуумной техники, как отмечалось выше, является электростатическое притягивание или отталкивание молекулярных диполей.

Общие черты поведения системы в целом являются усреднённым отражением движения отдельных молекул. Молекулы распределяются по возможным для них состояниям – их координаты (ради- ус-вектор) rG и скорости v принимают определённые значения в определенное время t.

Математически это описывается функцией распределения f (r , vG, t), характеризующей вероят-

ность пребывания частицы в данном состоянии. Рассматривается 6-мерное пространство в осях, на которых отложены значения координат и скоростей частиц системы; в статистической физике оно называется фазовым пространством.

Локальный объем пространства dV, по которому проводится осреднение характеристик отдельных молекул, должен быть достаточно мал, чтобы в его пределах действительно существовала изотропность распределения молекул и не изменялись внешние силы, действующие на молекулы при данном разрежении. Объем должен быть таков, чтобы в нем было не менее 100 молекул65. Заметим, что при улучшении вакуума величина dV увеличивается.

Умножив dP на полное число молекул в системе N, получим количество молекул dN, находящихся в объеме dV и имеющих скорости в указанном диапазоне:

Физический смысл функции распределения состоит в том, что она представляет концентрацию молекул n в малой области dV вокруг точки радиуса-вектора с координатами х, у, z, обладающих скоростями в указанном интервале d v, т.е.

где t – текущее время; х, у, z, vx, vу, vz – компоненты векторов и соответственно; или

65 dV ≤ 10–17 см3 при 105 Па или ≤ 1 см3 при 10–12 Па.

50