Красавин Компютерныы практикум в среде МатЛаб 2015

Рис. 18.1. Случайные числа, сгенерированные алгоритмом Метрополиса и имеющие гауссово распределение

Рис. 18.2. Гистограмма случайных чисел из рис. 18.1 и огибающая

1/

√10π

211

Задания

18.1.Вычислить автокорреляционную функцию для случайных чисел из примера 18.1. Определить значение , при котором случайные числа можно считать независимыми.

18.2.Исследовать зависимость числа успешных изменений конфигурации (под успешным изменением конфигурации

18.3. При помощи алгоритма Метрополиса сгенерировать последовательность случайных величин, имеющих нормальное распределение, выделить из этой последовательности подпоследовательность независимых случайных величин, и использовать эту подпоследовательность для расчета интегралов:

;

.

212

19

Фурье-преобразование

Рассмотрим периодическую функцию с периодом 1, определенную на всей действительной оси, и разложим ее в ряд Фурье:

,

где – целое, при этом для сходимости потребуем

слагаемых с одинаковыми экспоненциальными множителями.

переменной , принадлежащей дискретной сетке .

213

Таким образом, теперь задача рассматривается только на одном

Введем скалярное произведение двух функций на дискретной сетке:

1 , .

Множитель 1/ введен для корректного перехода в непрерывный предел:

вычислить скалярное произведение можно двумя способами:

214

Если коэффициенты быстро спадают с ростом номера , то

.

Для численного расчета всех коэффициентов Фурье в общем случае необходимо ~ операций, и при достаточно большом процедура расчета коэффициентов может занимать значительное время. Существует алгоритм, который позволяет проводить разложение в ряд Фурье гораздо быстрее – за ~ log операций – так называемое быстрое преобразование Фурье.

Пусть имеются коэффициенты Фурье некоторой периодической функции :

Тогда фурье-компоненту можно переписать так:

1

, .

216

Задача разбилась на две части: сначала определяют коэффициенты , а затем подставляют их в выражение для коэффициентов Фурье .

Определим количество операций, необходимое на расчет фурьекомпонент. Легко оценить, что для расчета всех коэффициентов

( операций). Таким образом, для расчета всех коэффициентов

~операций. В общем случае при разбиении числа

В MatLab быстрое преобразование Фурье реализуется при помощи функции fft. В примере 19.1 рассмотрено использование этой функции для восстановления зашумленного сигнала

(рис. 19.1).

Пример 19.1.

Fs = 100000; % Частота дискретизации

T = 1/Fs; % Дискретизация по времени

L = 10000; % Длина сигнала

t= (0:L-1)*T; % Вектор времени

%Сумма двух синусоид 500 и 1200 Гц

x= 0.7*sin(2*pi*500*t) + sin(2*pi*1200*t);

figure

% посторение графика зависимости амплитуды чистого сигнала от времени

subplot(2,2,1)

plot(Fs*t(1:1000),x(1:1000))

title('Исходный сигнал (2 синусоиды 500 и 1200 Гц)') xlabel('Время, мс')

% построение графика зависимости амплитуды зашумленного сигнала от времени

subplot(2,2,2)

plot(Fs*t(1:1000),y(1:1000)) title('Сигнал с шумом') xlabel('Время, мс')

Y = fft(y); % быстрое фурье-преобразование зашумленного сигнала f = Fs*linspace(0,1,L); % сетка по частотам

% построение спектра зашумленного сигнала в диапазоне частот [0

Гц, 2000 Гц] subplot(2,2,3)

plot(f(f<2000),abs(Y(f<2000))) title('Спектр сигнала с шумом')

218

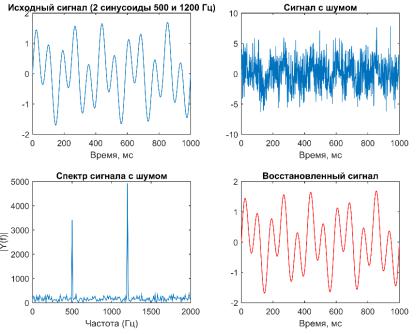
xlabel('Частота (Гц)') ylabel('|Y(f)|')

%нахождение двух основных пиков в спектре зашумленного сигнала в диапазоне частот [0 Гц, 2000 Гц]

[psor,lsor] = findpeaks(abs(Y(f<2000)), 'SortStr', 'descend', 'NPeaks', 2);

fr=f(lsor); x=0; % нахождение частоты пиков

for i=1:1:numel(fr) % цикл по частотам для восстановления сигнала x=x+psor(i)/max(psor)*sin(2*pi*fr(i)*t);

end

%посторение графика зависимости амплитуды восстановленного сигнала от времени

subplot(2,2,4)

plot(Fs*t(1:1000),x(1:1000),'r') title('Восстановленный сигнал') xlabel('Время, мс')

Рис. 19.1. Восстановление зашумленного сингала при помощи фурье-преобразования

219

В примере 19.2 рассматривается спектральный анализ аудиофайла на примере крика голубого кита (рис. 19.2).

Пример 19.2.

'bluewhale.au'); % ссылка на аудиофайл с голосом синего кита; этот файл поставляется вместе с системой MatLab

[x,fs] = audioread(whaleFile); % считывание аудиофайла sound(x,fs); % воспроизведение аудиофайла; файл может быть прослушан

figure % рис. 19.2 subplot(3,1,1)

t=10*(0:1/fs:(length(x)-1)/fs); % перевод дискретизации аудиофайла в сетку по времени

plot(t,x) % построение графика зависимости амплитуды от времени xlabel('Время, с')

ylabel('Амплитуда')

title('{\bf Крик голубого кита}')

subplot(3,1,2)

bCall = x(2.45e4:3.10e4); % bCall - "второе слово" голубого кита tb = 10*(0:1/fs:(length(bCall)-1)/fs); % перевод дискретизации

"второго слова" в сетку по времени

plot(tb,bCall,'m') % построение графика зависимости амплитуды от времени для "второго слова"

xlim([0 tb(end)]) % установление пределов графика по оси Х xlabel('Время, с')

ylabel('Амплитуда') title('{\bf Второе слово}')

subplot(3,1,3)

plot(f(1:floor(n/2)),p(1:floor(n/2)),'r') % построение графика зависимости мощности сигнала от частоты

xlabel('Частота, Гц') ylabel('Мощность')

220