Красавин Компютерныы практикум в среде МатЛаб 2015

Таким образом, задача сводится к системе линейных уравнений

ΨΨ,

собственных функций и собственных значений матрицы следует

ΦΦ ,

ΦΦ .

Процесс перехода к собственному базису называется диагонализацией матрицы , во многих современных математических пакетах имеются встроенные достаточно мощные процедуры диагонализации матриц, позволяющие находить собственные векторы и собственные числа произвольных матриц довольно больших размеров. Результатом процедуры диагонализации будет вектор-столбец собственных значений гамильтониана, или спектр системы,

… ,

а также матрица , состоящая из вектор-столбцов, отвечающих разложению собственных функций Φ по исходному базису Φ:

161

ΦΦ .

Впримере 14.1 приведен код, реализующий решение уравнения Шредингера для частицы в бесконечной яме.

Пример 14.1.

function [H,E] = InfiniteWell(a,n,k)

%Входные параметры:

%a - ширина ямы

%n - число отрезков

%k - число решений

%Выходные параметры:

%H – матрица гамильтониана

%E – спектр

h = a/n; % ширина отрезка

x = [h/2 : h : a - h/2]; % координаты середин отрезков

% создание матрицы H

H = zeros(n); % инициализация; квадратная матрица из нулей

H = H + (1/h^2)*diag(ones(1,n)); % добавление главной диагонали H = H - (1/2/h^2)*diag(ones(1,n-1),1); % добавление верхней

диагонали

H = H - (1/2/h^2)*diag(ones(1,n-1),-1); % добавление нижней диагонали

% диагонализация матрицы H

[V,E] = eigs(H,k,0); % eigs – функция диагонализации матрицы; первый параметр – исходная матрица; второй параметр – число решений, которые нужно найти; третий параметр – область поиска, найденные решения будут располагаться вблизи этого числа

%E - матрица размера k x k с собственными значениями по главной диагонали

%V - матрица размера n x k разложения собственных функций по базисным

162

[E,DE] = sort(diag(E)); % превращение диагональной матрицы E в вектор и сортировка его элементов

%нормировка матрицы V A = sum(V(:,1).^2)*h; V = V / sqrt(A);

%построение графиков собственных функций col = 'bgrcmk'; % обозначения цветов

figure

for i = 1 : k subplot(3,2,i)

plot(x,V(:,DE(i)).^2,col(i),'LineWidth',3) % численное решение hold on

plot(x,2*(sin(pi*i*x)).^2,'ok') % точное решение set(gca, 'LineWidth',1)

set(gca, 'FontName', 'Trebuchet MS') set(gca, 'FontSize', 8)

set(gca, 'FontWeight', 'bold')

xlabel('x', 'FontName', 'Trebuchet MS', 'FontAngle', 'italic', 'FontSize', 10, 'FontWeight', 'bold')

ylabel('y', 'FontName', 'Trebuchet MS', 'FontAngle', 'italic', 'FontSize', 10, 'FontWeight', 'bold') title(['E=',num2str(E(i))],'FontSize', 12)

end

В результате выполнения программы вычисляется спектр частицы в бесконечной потенциальной яме (собственные числа гамильтониана) и квадраты модулей волновых функций частицы (собственных функций гамильтониана, рис. 14.3), которые также сравниваются сточным решением

сплошными линиями на рис. 14.3, точные решения – черными кругами. Хотя точность численного решения довольно высока, особенно для основного состояния с энергией , видно, что с увеличением номера энергетического уровня погрешность расчета возрастает. Следует также отметить, что при решении одночастичных задач всегда справедлива осцилляционная теорема,

утверждающая, что число нулей собственной волновой функции на единицу меньше, чем номер энергетического уровня, которому она отвечает (при этом не учитываются вырожденные состояния).

163

Рис. 14.3. Квадраты модулей волновых функций частицы

вбесконечной потенциальной яме

14.3.Конечная потенциальная яма

Рассмотрим теперь задачу о частице в конечной потенциальной яме (рис. 14.4), где

164

В яме конечной глубины состояния частицы делятся на

связанные состояния и состояния непрерывного спектра ,

энергия которых удовлетворяет соотношению:

min ∞ .

Рис. 14.4. Конечная потенциальная яма

Собственные волновые функции, отвечающие значениям энергии из непрерывного спектра, за пределами ямы ведут себя как плоские волны:

Ψconst ,

асобственные волновые функции, отвечающие связанным

связанных состояний недостаточно ограничиваться лишь размерами ямы, так как волновые функции существуют и при

. Граница области , на которой ищется решение, должна быть определена из условия затухания полученного решения на

конечное значение в точке , то следует увеличить размер области, на которой ищется решение, и решить задачу заново.

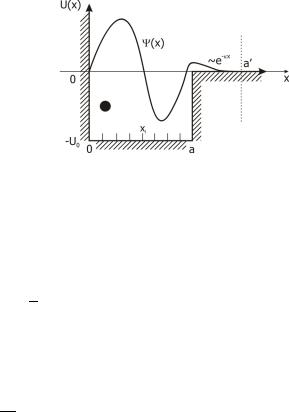
Рис. 14.5. За пределами ямы волновые функции, отвечающие связанным состояниям, экспоненциально затухают

По сравнению с задачей о яме с бесконечными стенками теперь спектральная задача формулируется следующим образом:

166

решений, отвечающих состояниям непрерывного спектра. При численной диагонализации матрицы это может привести к проблеме, связанной с тем, что матрица может быть плохо обусловленной, т.е. некоторые ее столбцы будут являться почти линейно зависимыми. Степень обусловленности матрицы характеризуется числом обусловленности, которое для симметричной вещественной матрицы равно отношению модулей максимального и минимального собственных значений. Большие числа обусловленности (порядка 1000 и больше) отвечают плохо обусловленным матрицам, при численной диагонализации которых возникают очень большие погрешности, приводящие к неверным результатам. Из-за того, что значения энергии частицы, отвечающие состояниям непрерывного спектра, могут принимать

математических пакетах имеются встроенные процедуры оценки числа обусловленности матриц до их диагонализации.

Для уменьшения числа обусловленности матрицы можно использовать следующий прием. Сдвинем всю потенциальную картину на рис. 14.5 на достаточно большую величину 0, так что

| | | |,

167

и, соответственно, к каждому элементу, стоящему на главной диагонали матрицы , добавится слагаемое, равное :

,

а на собственные функции сдвиг потенциальной картины не окажет влияния:

ΨΨ.

Впримере 14.2 приведен код, реализующий решение уравнения Шредингера для частицы в конечной яме.

Пример 14.2.

function [H,E] = FiniteWell(a,a1,n,k,U0)

%Входные параметры

%a - ширина ямы

%a1 - область решения

%n - число отрезков

%k - число решений

%U0 - глубина ямы

%Выходные параметры

%H – матрица гамильтониана

%E – спектр системы

h = a1/n; % ширина отрезка

x = [h/2 : h : a1 - h/2]; % координаты середин отрезков

% создание матрицы H

H = zeros(n); % инициализация

H = H + (1/h^2)*diag(ones(1,n)); % добавление главной диагонали

168

H = H - (1/2/h^2)*diag(ones(1,n-1),1); % добавление верхней диагонали

H = H - (1/2/h^2)*diag(ones(1,n-1),-1); % добавление нижней диагонали

b = find(x < a); % нахождение номеров отрезков, попадающих в яму

U = zeros(size(x)); % инициализация массива U(x)

U(b) = -U0; % для отрезков, попадающих в яму, значение потенциала равно -U0

H = H + diag(U); % добавление потенциала ямы в матрицу H

% диагонализация матрицы H

[V,E] = eigs(H,k,-U0); % первый параметр - матрица H; второй параметр - число решений; третий параметробласть поиска этих решений - дно ямы

%E - матрица размера k x k с собственными значениями по главной диагонали

%V - матрица размера n x k разложения собственных функций по

базисным

[E,DE] = sort(diag(E)); % превращение диагональной матрицы в вектор и сортировка его элементов

%нормировка матрицы V A = sum(V(:,1).^2)*h; V = V / sqrt(A);

%построение графиков собственных функций col = 'bgrcmk';

figure

for i = 1 : k

subplot(3,2,i)

plot(x,V(:,DE(i)).^2,col(i),'LineWidth',2) % численное решение

set(gca, 'LineWidth',1)

set(gca, 'FontName', 'Trebuchet MS') set(gca, 'FontSize', 8)

set(gca, 'FontWeight', 'bold')

xlabel('x', 'FontName', 'Trebuchet MS', 'FontAngle', 'italic', 'FontSize', 10, 'FontWeight', 'bold')

ylabel('y', 'FontName', 'Trebuchet MS', 'FontAngle', 'italic', 'FontSize', 10, 'FontWeight', 'bold')

title(['E=',num2str(E(i))],'FontSize', 12)

hold on

plot(x,U/U0,'k','LineWidth',3) % профиль ямы (не в масштабе) plot(x(b),E(i)/U0*ones(size(x(b))),col(i),'LineWidth',2)

end

169

В результате выполнения программы вычисляется спектр частицы в конечной потенциальной яме (собственные числа гамильтониана) и квадраты модулей

состояний частицы в такой яме являются связанными, а шестое принадлежит к непрерывномуспектру.

Рис. 14.6. Частица в конечной потенциальной яме. Показаны квадраты модулей волновых функций, значения энергии частицы, атакже профиль ямы

(не в масштабе)

170