Маслов Введение в физику ноноструктур 2011

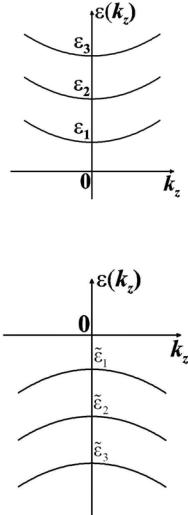
су дырки, а высота энергетического барьера, определяющего вид дискретного спектра в поперечном направлении, равна не EC, а

EV.

Рис. 6.3. Энергетический спектр электронов в полупроводниковой квантовой нити. За начало отсчета принята энергия дна зоны проводимости в полупроводнике А

Рис. 6.4. Энергетический спектр дырок в полупроводниковой квантовой нити. За начало отсчета принята энергия потолка валентной зоны в полупроводнике А

41

Плотность электронных состояний g(ε) в квантовой нити представляет собой сумму вкладов от всех зон размерного квантования:

где n – номер зоны. Она изображена на рис. 6.5. Аналогичный вид имеет и плотность состояний для дырок. По мере увеличения концентрации носителей в квантовой нити сначала заполняется первая зона размерного квантования, затем – вторая (первая при этом тоже продолжает заполняться) и т. д.

Рис. 6.5. Плотность электронных состояний в полупроводниковой квантовой нити. Энергия отсчитывается от дна зоны проводимости полупроводника А

Наиболее просто изготовить квантовую нить из двумерного электронного газа. Для этого нужно приложить напряжение к электроду, имеющему соответствующую форму и расположенному на границе раздела формирующих двумерный электронный газ полупроводников, см. рис. 6.6. При этом потенциальная энергия электронов уменьшается в области, имеющей форму длинной полоски. В этой области и скапливаются электроны. Эффективной глубиной потенциальной ямы для электронов можно управлять, изменяя напряжение на электроде. Такие квантовые нити называются “gate defined quantum wires”. Их недостатком является плохая воспроиз-

42

водимость результатов, что отчасти связано с отсутствием у них четко определенной границы.

Рис. 6.6. Квантовая нить в двумерном электронном газе

Упомянем и еще один способ изготовления полупроводниковых квантовых нитей, который достаточно сложен в реализации, но позволяет получать очень качественные квантовые нити, используя метод молекулярно-лучевой эпитаксии. На первом этапе из двух полупроводников изготавливается квантовая яма A/B/A с EgA > EgB. Затем в плоскости, перпендикулярной квантовой яме, делается скол, а на поверхность скола напыляется сначала тонкий слой полупроводника В, а затем – толстый слой полупроводника А. При этом квантовая нить формируется в области пересечения двух взаимно перпендикулярных квантовых ям. Такие квантовые нити называют Т-образными (T-shaped), а метод их изготовления – методом заращивания поверхности скола (cleaved edge overgrowth, CEO).

43

7. Энергетический спектр электронов в квантовых нитях, полученных методом заращивания поверхности скола. Баллистическая проводимость квантовых нитей

Покажем, что в электронном энергетическом спектре квантовой нити, полученной методом заращивания поверхности скола, имеется по крайней мере одна подзона размерного квантования, в которой электронные состояния локализованы в двух направлениях и делокализованы в одном. Квантовая нить образуется в области пересечения двух полупроводниковых квантовых ям, изготовленных из полупроводников А и В, таких что дно зоны проводимости полупроводника В лежит ниже дна зоны проводимости полупроводника А, то есть ECВ < ECA, см. рис. 7.1. При этом потенциальная энергия добавленного в наноструктуру “лишнего” электрона равна:

U (rG) = EC (rG) = ECB при r B;

ECA при rG A.

где EC = ECA – ECB – разрыв зон проводимости полупроводников А и В.

Рис. 7.1. Поперечное сечение квантовой нити, полученной методом заращивания поверхности скола. Потенциальная энергия электрона равна нулю в области, занимаемой полупроводником В, и разрыву зон проводимости EC = ECA – ECB в полупроводнике А

44

Поскольку потенциальная энергия электрона зависит только от x и y, см. рис. 7.1, то в приближении эффективной массы решение уравнения Шредингера для огибающей функции

можно искать в виде: Ψ(r) = ϕ(x, y)φ(z), где функции ϕ и φ удовлетворяют уравнениям:

ε1 + ε2 = ε.

Обозначим: ε2 = =2kz2 2m *. Тогда для функции φ(z) найдем:

φ(z) = L−1/2 exp(ikz z),

где L – длина квантовой нити. Таким образом, электронные состояния делокализованы вдоль оси z. Это есть следствие однородности рассматриваемой наноструктуры вдоль оси z. Вопрос, однако, заключается в том, существуют ли локализованные состояния электрона в плоскости xy. Если да, то энергия εn каждого такого состояния является дном соответствующей подзоны размерного квантования, в которой закон дисперсии имеет вид:

На первый взгляд кажется, что локализованные в плоскости xy состояния отсутствуют, поскольку в структуре нет барьеров, препятствующих удалению электрона на бесконечно большое расстояние от области пересечения квантовых ям. Но мы покажем, что это не так.

Несмотря на сравнительно простой вид двумерного потенциального рельефа, уравнение Шредингера для функции ϕ(x,y) аналитически не решается, поэтому для доказательства наличия локализованных в плоскости xy состояний воспользуемся следующей моделью. Рассмотрим две пересекающиеся цепочки атомов: одну –

45

бесконечную, а другую – полубесконечную (см. рис. 7.2), что соответствует квантовой нити, образованной на стыке двух квантовых ям толщиной в один атомный слой каждая, и бесконечно большому разрыву зон проводимости EC.

X

1

2

3

4

5

Y m

Рис. 7.2. Две пересекающиеся цепочки атомов – модель поперечного потенциального рельефа электрона в квантовой нити

Принимая атомный уровень за начало отсчета энергии и обозначая через t матричный элемент перескока электрона между соседними атомами, получим в приближении сильной связи следующую

орбиталям:

EAi = t∑Aj ,

j

где суммирование ведется по всем атомам j, являющимся ближайшими соседями атома i. Решение этой системы дает для энергии и волновой функции основного состояния:

E = − 32 t,

46

Таким образом, волновая функция экспоненциально быстро убывает по мере удаления от начала координат, а значит – описывает локализованное состояние. Заметим, что такое состояние только одно (за ним следует непрерывный спектр), то есть в квантовой нити имеется одна подзона размерного квантования с делокализованными вдоль оси квантовой нити волновыми функциями.

Для определения электрической проводимости квантовой нити можно воспользоваться, например, формулой Друде. Заметим, однако, что эта формула применима к системам, размеры которых значительно больше длины l свободного пробега электронов в материале, из которого они изготовлены, так что электроны на своем пути многократно рассеиваются. Рассмотрим короткую квантовую нить, длина L которой меньше длины свободного пробега. Тогда электроны будут “пролетать” через нее, как снаряды из пушки. Такие наноструктуры называются баллистическими, а их проводимость – баллистической. Она определяется как коэффициент пропорциональности между силой тока через квантовую нить I и приложенным к ней небольшим “измерительным” напряжением V:

I= GV .

Вотличие от удельной проводимости (conductivity) σ, величина G измеряется в Ом–1. Ее также называют кондактансом (conductance).

Рассчитаем проводимость квантовой нити. Будем считать, что

нам известен набор дискретных уровней энергии εn для движения электрона в перпендикулярном оси квантовой нити направлении, то есть известна ее электронная структура:

Если к квантовой нити приложено напряжение V, то в переносе тока участвуют те электроны, энергия которых лежит в интервале μ ≤ ε ≤ μ + eV (где μ и μ + eV – химические потенциалы электриче-

ских контактов к квантовой нити), которые при этом движутся в сторону контакта с меньшим химическим потенциалом, и для которых в квантовой нити есть доступные делокализованные состояния (то естьε > ε1 ), см. рис. 7.3. Время, затрачиваемое электроном с

импульсом pG на прохождение квантовой нити, равно t = Lvz = m * L pz .

47

“квант проводимости” (а обратную ей величину – “квант сопротивления”, он составляет около 10 кОм). На практике квантование проводимости квантовой нити наблюдают, прикладывая к ней напряжение U (порядка 1 В, в отличие от маленького “измерительного” напряжения V ~ 1 мкВ). При этом система уровней размерного квантования (вместе с соответствующими подзонами) смещается относительно уровня Ферми. Из-за конечной величины температуры и других факторов зависимость G от U имеет вид ступенек со скругленными краями, см. рис. 7.4.

Рис. 7.4. Зависимость проводимости G квантовой нити от напряжения U на управляющем электроде

Обычно для экспериментов используют не квантовую нить, а так называемый квантовый точечный контакт (quantum point contact, QPC) – сужение в двумерном электронном газе, см. рис. 7.5.

Рис. 7.5. Квантовый точечный контакт в двумерном электронном газе (2DEG)

49

8. Полупроводниковые квантовые точки. Энергетический спектр кубических квантовых точек. Способы изготовления квантовых точек. Энергетический спектр квантовых точек с двумерным и трехмерным потенциалами конфайнмента. Кулоновское взаимодействие электронов в квантовых точках. Искусственные молекулы

Полупроводниковые квантовые точки – типичные представители нульмерных наноструктур: у них все три характерных размера имеют порядок нанометра. Рассмотрим в качестве примера кубическую квантовую точку, представляющую собой куб из полупроводника В, окруженный со всех сторон полупроводником А, таким что дно зоны проводимости полупроводника В лежит ниже дна зоны проводимости полупроводника А, то есть ECВ < ECA, см. рис. 8.1.

Рис. 8.1. Кубическая квантовая точка из полупроводника В в полупроводнике А

(ECВ < ECA)

При этом потенциальная энергия добавленного в наноструктуру “лишнего” электрона равна:

U (rG) = EC (rG) = ECB при r B;

ECA при rG A.

Принимая величину ECВ за начало отсчета энергии, получим: