
Маслов Введение в физику ноноструктур 2011
.pdf
довольно существенно (в 10 и более раз) отличаться от нее в ту или иную сторону.
Периодические граничные условия Ψk (x)= Ψk (x + L) приводят
к тому, что величина k может принимать не любые значения (как в бесконечном пространстве –∞ < x < +∞), а лишь дискретные: kn = 2πn L, где n = 0; ±1; ±2; … – целые числа. Соответственно, энергетический спектр свободного электрона имеет вид:
L, где n = 0; ±1; ±2; … – целые числа. Соответственно, энергетический спектр свободного электрона имеет вид:
εn |
= ε(kn ) = =2kn2 |
/ 2m = (=2 / 2m)(2π/ L)2 n2 . |
Заметим, что |
k = kn+1 − kn |
= 2π L →0 и Δεn = εn+1 −εn →0 при |
L → ∞, то есть в макроскопической системе энергетический спектр
является, по существу, не дискретным, а квазинепрерывным. Тем не менее (в отличие от непрерывного спектра) можно “пересчитать” электронные состояния (и количество электронов в них), что часто бывает удобно.
Рассмотрим систему, в которой имеется макроскопическое число электронов Nel >> 1. При нулевой температуре полная энергия всей системы должна иметь минимальную возможную величину (основное состояние). Так будет, если электроны занимают уровни с энергией ε(k) ==2k2 / 2m ≤εF , где εF ==2kF2 / 2m – энергия Ферми, kF – волновой вектор Ферми. Все состояния с −kF ≤ k ≤ kF при
этом заняты, а состояния с k > kF – свободны. С учетом того, что в
состоянии с данным k могут находиться два электрона (со спином “вверх” и “вниз”), получим для полного числа электронов:
Nel = ∑ 2 . Характеристики макроскопической системы не чувст-
|k|≤kF
вительны к виду граничных условий, поэтому выберем их периодическими. При этом “расстояние” k = 2π L между соседними значениями k очень мало, то есть энергетический спектр является квазинепрерывным, и можно перейти от суммы по kn = 2πn
L между соседними значениями k очень мало, то есть энергетический спектр является квазинепрерывным, и можно перейти от суммы по kn = 2πn L к
L к
|
∫ |
|
k |
|
2π |
∫ |
|
интегралу по k: |
Nel = kF |
2 |
dk |
= |
L |
kF |
2dk. Концентрация электро- |
|
|
|
|||||
|
−kF |
|
|
|
|
−kF |
|
нов n = Nel L = 2kF π. Величина kF |
монотонно увеличивается с |
||||||
|
|
|
|
11 |
|
|
|
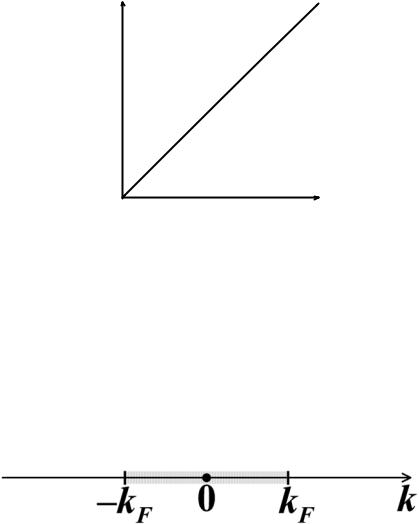
ростом n, так как при увеличении числа электронов заполняются состояния с большей энергией, см. рис. 2.1.
kF
0 |
n |
Рис. 2.1. Зависимость концентрации электронов n в одномерном свободном электронном газе от волнового вектора Ферми kF
|
Поверхностью |
Ферми называется множество точек в |
kG |
-пространстве, |
удовлетворяющих условию ε(kG)= εF , где εF – |
энергия Ферми. При T = 0 все состояния с ε(kG)≤ εF заняты элек-
тронами, а состояния с ε(kG)>εF свободны. В одномерном слу-
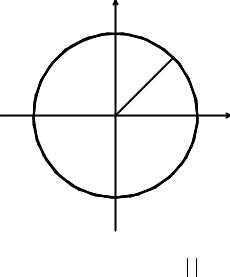
чаеkG = keGx и ε(kG)==2k2 / 2m , поэтому “поверхность” Ферми представляет собой две точки: k = kF и k = −kF , см. рис. 2.2.
Рис. 2.2. При T = 0 электроны в одномерном свободном электронном газе занимают состояния с проекцией волнового вектора −kF ≤ k ≤ kF на ось x
12

Плотностью электронных состояний g(ε) называется отношение числа состояний в “физически малом” интервале энергий [ε; ε+dε] к величине этого интервала dε. Для электрона с заданной проекцией спина “плотность состояний на спин” равна g (ε) = ∑δ(ε −εn ),
n
где δ(x) – дельта-функция, n – набор квантовых чисел (исключая спиновое квантовое число), εn – собственные значения энергии электрона, которые находятся из решения уравнения Шредингера для рассматриваемой системы. Для одномерного электронного газа квантовым числом n можно считать проекцию k волнового вектора
на ось x. При этом εn =ε(k) ==2k2 / 2m. Переходя от суммы по n к интегралу по k, получим:
|
m |
|
1/2 |
−1/2 |
|
||
g (ε)= L |
|
|
|
|
ε |
|
θ(ε), |
2 |
= |
2 |
|
||||
|
2π |
|
|
|
|
|
|
где θ(ε) – тета-функция: θ(ε)= 1 при ε > 0 и θ(ε)= 0 при ε < 0.
Плотность состояний расходится корневым образом при ε → 0 и монотонно уменьшается с ростом ε, см. рис. 2.3 (напомним, что для свободных электронов в трехмерном пространстве g (ε)~ ε1/2θ(ε)).
g(ε)
0 |
ε |
Рис. 2.3. Плотность электронных состояний одномерного свободного электронного газа с законом дисперсии ε(k) = =2k2 / 2m
13

Так как мы считали потенциальную энергию электронов равной
нулю, то ε(k) ==2k2 / 2m ≥0. |
|
Если же U(x)=Ec – отличная от нуля |
|||||
константа, то ε(k) = Ec |
+=2k2 / 2m ≥ Ec . |
Плотность состояний при |
|||||
этом равна: |
|
|
|
|
|
|
|
g (ε)= L |
|
m |
|
1/ 2 |
(ε − E )−1/2 θ(ε− E ), |
||
|
2 |
|
2 |
|
|||
|
= |
c |
c |
||||
|
|
2π |
|
|
|
|
|
см. рис. 2.4.
g(ε)
0 Ec |
ε |
Рис. 2.4. Плотность электронных состояний одномерного свободного электронного газа с законом дисперсии ε(k) = Ec +=2k2 / 2m
Используем плотность состояний для расчета зависимости концентрации электронов n от волнового вектора Ферми kF. Поскольку 1) по определению плотности состояний, величина g(ε)dε равна числу состояний электрона с одной проекцией спина в интервале энергий [ε; ε+dε] и 2) при T = 0 электроны занимают все состояния
с энергией ε(k )≤ εF , причем в каждом состоянии, в соответствии с
принципом Паули, находятся два электрона (со спином “вверх” и
εF
“вниз”), то полное число электронов в системе Nel = 2 ∫ g(ε)dε.
−∞
Область энергий ε < 0 не дает вклада в интеграл, так как g(ε) = 0
14

при ε < 0. Вычисляя интеграл, получим n = Nel/L = 2kF/π, как и вы- |
|||||||||
ше. Полная энергия всей системы электронов при T = 0 (энергия |
|||||||||
|
|
ε |
εg(ε)dε = 1 |
|
|
|
|
||
основного состояния) равна E0 |
= 2 ∫F |
εF Nel , тогда как в |
|||||||
|
|
−∞ |
|
|
3 |
|
|
|
|
трехмерном свободном электронном газе E = |
3 ε |
F |
N |
el |
. |
||||
|
|
|
|
0 |
5 |
|
|
||
При T ≠ 0 среднее число электронов с одной проекцией спина в |
|||||||||
состоянии с энергией ε равно: |
|
ε−μ +1 −1 |
|
|
|
|
|
||
f (ε,T ) = exp |
, |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
kBT |
|
|
|
|
|
|
|
где f (ε,T ) – функция распределения Ферми–Дирака (см. рис. 2.5), |
|||||||||
μ – химический потенциал. |
|
|
|
|
|
|
|
|
|
f(ε,T) |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
εF |
|
|
ε |
|
|
Рис. 2.5. Функция распределения Ферми-Дирака |
f (ε,T ) при T = 0 (сплошная |
||||||||
линия) и kBT = μ 10 (пунктирная линия) |
|
|
|
||||||
Число электронов в состояниях с энергиями, принадлежащими интервалу [ε; ε + dε], равно удвоенному (с учетом спина) произведению f (ε,T ) на число состояний g(ε)dε в этом интервале. Следо-
вательно, полное число электронов Nel = 2 |
∞∫ f (ε,T )g(ε)dε. Это со- |
|
−∞ |
15 |
|

отношение неявно определяет μ как функцию T. В отличие от случая T = 0, верхний предел интегрирования равен бесконечности, так как при T ≠ 0 электроны могут с конечной вероятностью f (ε,T ) занимать энергетические уровни с ε > εF. Вычисление
интеграла дает
|
|
|
π |
2 |
|
kBT |
2 |
|
μ(T ) ≈ εF |
1 |
+ |
|
|
|
|
||
|
|
|
||||||
|
|
|
12 |
|
εF |
|
|
|
|
|
|
|
|||||
при kBT << εF , см. рис. 2.6. Так как обычно εF ~ 1 эВ, то неравенство kBT << εF справедливо даже при T ~ 1000 К. Заметим, что μ уве-
личивается с ростом T – в отличие от свободного трехмерного электронного газа.
μ
εF
|
|
|
|
0 |
kBT |
||
εF
Рис. 2.6. Температурная зависимость химического потенциала μ одномерного свободного электронного газа при kBT << εF
Полную энергию E одномерного свободного электронного газа при T ≠ 0 можно найти, заметив, что энергия электронов в состояниях из интервала [ε; ε + dε] равна произведению ε на число элек-
16

тронов 2 f (ε,T )g (ε)dε во всех этих состояниях. Тогда
∞
E(T ) = 2 ∫ εg(ε) f (ε,T )dε, и мы получим:
−∞
E(T ) ≈ E0 1+ π42 kεBFT 2 .
Зависимость E(T) приведена на рис. 2.7.
E
E0
0 kBT
εF
Рис. 2.7. Температурная зависимость полной энергии E одномерного свободного электронного газа при kBT << εF
17
3. Свободный двумерный электронный газ. Плотность состояний. Энергия Ферми. Химический потенциал. Полная энергия
Электронные свойства ряда двумерных наноструктур (например, квантовых ям) можно качественно (а иногда и количественно) описать в рамках модели свободного двумерного электронного газа. Будем считать, что двумерная наноструктура имеет форму квадрата с размерами L ×L (здесь L – макроскопический размер), а ее толщина равна нулю. Электроны занимают область 0 < x, y < L, причем их потенциальная энергия в этой области U(x,y) = 0, то есть они являются свободными. Решение уравнения Шредингера
|
= |
2 |
|
2 |
Ψ(x2 , y) |
|
2 |
Ψ(x2 , y) |
|
|
− |
|
|
∂ |
+ |
∂ |
|
= εΨ(x, y) |
|||
|
|
|
|
|||||||
|
2m |
|
∂x |
|
|
∂y |
|
|
||
имеет вид (с учетом нормировки квадрата модуля волновой функции на единицу):
|
G |
−1 |
GG |
G |
=2kG2 |
|
=2 (kx2 + ky2 ) |
|
|
ΨG |
(ρ) = L |
exp(ikρ); ε(k) = |
|
= |
|
, |
|||
2m |
2m |
||||||||
k |
|
|
|
|
|
|
|||
где ρG = xeGx + yeGy |
|
|
|
|
|
||||
– двумерный радиус-вектор, k = kxeGx + ky eGy – дву- |
|||||||||
мерный волновой вектор электрона (он является “квантовым числом”, определяющим вид волновой функции и закона дисперсии), m – эффективная масса электрона.
Периодические граничные условия по обоим направлениям,
ΨG |
(x, y) = ΨG |
(x + L, y) = ΨG |
(x, y + L) , приводят к дискретности |
k |
k |
k |
|
компонент волнового вектора kx = 2πn1/L, ky = 2πn2/L, где n1 и n2 –
целые числаG . ЭнергетическийG спектр является квазинепрерывным:
εn1n2 = ε(k) = =2k2 / 2m = (=2 / 2m)(2π/ L)2 (n12 + n22 ). Заметим, что для другого вида граничных условий (например, периодических по оси x и антипериодических по оси y) допустимые значения волнового вектора и энергии будут другими, но их плотность (в обратном и энергетическом пространстве, соответственно) останется такой же.
Если в системе имеется макроскопическое число электронов
Nel >>1, то при нулевой температуре они занимают состояния с
G G
энергией ε(k) ==2k2 / 2m ≤εF , где εF ==2k F2 /2m – энергия Ферми, 18
kFG – волновой вектор Ферми. |
При этом заняты все состояния с |
| k |≤ kF , а состояния с | k |> kF |
свободны. Поверхность Ферми, оп- |
ределяемая условием ε(k) =εF |
(то есть | k |= kF ), имеет вид окруж- |
ности с радиусом kF, см. рис. 3.1. В двумерной системе поверхность Ферми называют обычно контуром Ферми.
ky
kF
0 kx
Рис. 3.1. При T = 0 электроны в двумерном свободном электронном газе занимают состояния с волновым вектором kG ≤ kF
С учетом того, что в состоянии с данным k могут находиться два электрона (со спином “вверх” и “вниз”), получим для полного числа электронов:
Nel = ∑G |
|
|
2 = |
∫∫ |
dk |
x |
|
dky |
2 |
= |
L2 |
|
|
∫∫ dkx dky 2, |
||
|
) |
k k |
(2π) |
2 |
G |
|||||||||||
k |
,k |
(|k|≤k |
F |
G |
|
|
|
|
|
|||||||
x |
y |
|
|
|k|≤kF |
|
|
|
|
|
|
|
|
|k|≤kF |
|||
где k = 2π/L. Переходя в полярные координаты и вычисляя интеграл, имеем для концентрации электронов: n = Nel  L2 = kF2
L2 = kF2  2π. Как
2π. Как
и в одномерном свободном электронном газе, концентрация электронов увеличивается с ростом kF, но по другому закону, см. рис. 3.2.
19

kF
0 |
n |
Рис. 3.2. Зависимость концентрации электронов n в двумерном свободном электронном газе от волнового вектора Ферми kF
Для плотности электронных состояний g(ε) двумерного свобод-
ного электронного газа получим: |
=2kG2 |
|
|
|
|
|
g(ε) = ∑δ(ε −εn ) = ∑δ(ε − |
2 |
m |
|
|
||
|
) = L |
|
|
θ(ε), |
||
2m |
2π= |
2 |
||||
n |
kG |
|
|
|
||
см. рис. 3.3.
g(ε) |
|
0 |
ε |
Рис. 3.3. Плотность электронных состояний двумерного свободного электронного газа с законом дисперсии ε(kG) = =2kG2 / 2m
20
