2. ЗАКОНЫ НЬЮТОНА

При решении задач этого раздела следует руководствоваться основными положениями.

1.Существуют такие системы отсчёта (их называют инерциальными), в которых тело, не взаимодействующее с другими телами, движется равномерно и прямолинейно. Это утверждение носит название закона инерции, или первого закона Ньютона. В дальнейшем будут использоваться, если не оговорено особо, только инерциальные системы отсчёта.

2.Если тело взаимодействует с другими телами, то его движение уже не будет равномерным и прямолинейным. Иными словами, скорость тела будет изменяться, т.е. тело будет двигаться с ускорением.

3.Всякое взаимодействия тел характеризуется силой. Ускорение тела пропорционально сумме сил, действующих на это тело:

ma = ΣF.

Это уравнение носит название второго закона Ньютона. Здесь m – масса частицы, a – вектор её ускорения, ΣF – векторная сумма сил, действующих на частицу со стороны других тел. Отметим здесь, что если в задаче рассматривается движение нескольких тел, то для каждого из них необходимо записать своё уравнение второго закона Ньютона. При этом система отсчёта может быть выбрана одной для всей системы тел, а можно для каждого тела выбирать свою систему отсчёта.

26

5. Если поверхности шероховатые, то сила реакции уже не будет перпендикулярна касательной плоскости. Её компонента, параллельная касательной плоскости, называется силой трения. Причем сила трения возникает либо при попытке сдвинуть одно тело по отношению к другому, либо при скольжении одного тела по поверхности другого. Следует различать два случая, когда встречается сила трения. Рассмотрим тело, находящееся на горизонтальной поверхности. Пусть к телу приложена сила F, направленная горизонтально.

Случай 1. Тело покоится относительно поверхности. Тогда сумма сил, приложенных к телу, равна нулю. Спроецировав силы, действующие на тело, на вертикальное и горизонтальное направление, получим, что сила тяжести уравновешивается нормальной составляющей силы реакции поверхности. А горизонтальная составляющая силы реакции, т.е. сила трения покоя, равна по величине и противоположна по направлению внешней силе F, направленной вдоль поверхности, на которой находится тело. Сказанное иллюстрируется рис. 2.2, на котором

где N – величина нормальной состав-

ляющей силы реакции поверхности, k – коэффициент трения между телом и поверхностью. Считается также, что:

6. Силы взаимодействия между телами равны по величине, противоположны по направлению и действуют вдоль одной прямой (третий закон Ньютона).

27

Задача 2.1. На горизонтальном столе находятся два бруска с массами m1 и m2, связанные невесомой, нерастяжимой нитью. Брусок m1 тянут с силой F, направленной параллельно столу. Коэффициент трения между брусками и столом – k. Найти ускорение, с которым движутся бруски и силу натяжения нити, связывающей их.

Решение. На рис. 2.3 изображены силы, действующие на каждое из тел. Так как нить предполагается нерастяжимой, то тела движутся с одинаковыми скоростями и, следовательно, с одинаковыми ускорениями. Составим уравнения второго закона Ньютона для каждого тела:

Рис. 2.3

Выберем систему координат XOY так, чтобы ось ОХ была направлена горизонтально, а ось OY – вертикально. Записывая (1) и

Мы получили четыре уравнения для семи неизвестных: ах, T1, Т2, N1, N2, Fтр1, Fтр2. Для того чтобы эта система имела единственное решение, необходимы еще три уравнения. Первое из этих трех уравнений получим, если помимо нерастяжимости нити учтем еще и её невесомость. Так как нить нерастяжима, то ее ускорение равно ускорению тел, которые она соединяет. Тогда уравнение второго закона Ньютона для нити имеет вид:

mн ax = T1 – T2,

28

где mн – масса нити, T1 и T2 – силы, приложенные к нити со стороны первого и второго тел соответственно. Так как нить невесома,

то mн = 0 и T1 – T2 = 0, т.е. T1 = T2.

Иными словами, нерастяжимая невесомая нить действует с одинаковыми силами на тела, которые она соединяет. Причем силы эти направлены вдоль нити. В дальнейшем мы этот результат будем постоянно использовать и не делать различия между T1 и T2, обозначая их одной буквой, скажем, Т. Равенство T1 = T2 одно из трех недостающих уравнений. Нам нужны еще два уравнения. Для их получения рассмотрим силы трения. Возможны, очевидно, два случая.

Случай 1. Тела движутся, поэтому: Fтр1 = kN1, Fтр2 = kN2. Тогда с учетом этих соотношений имеем вместо (3)–(6) следующую сис-

тему уравнений:

Проанализируем полученное выражение для ах. Это следует делать всегда, но особенно в тех случаях, когда результат не является знакопостоянной величиной (т.е. в нём где-то содержится разность некоторых величин). Так как результат для ах получен в предположении, что тела движутся, то очевидно, что ах должно быть положительной величиной:

ax = m1 F+ m2 − kg > 0 ,

откуда F > kg (m1+ m2).

29

Если же это неравенство нарушается, т.е. F < kg (m1+ m2), то тела, очевидно, покоятся. Рассмотрим этот случай.

Случай 2. Тела покоятся, поэтому ах = 0. Из (3)–(6) получаем то-

гда

Если увеличивать F, то будет возрастать и сила трения Fтрпокоя1 ,

до тех пор, пока она не станет равной km1g. Поэтому если

kg (m1+ m2) > F > km1g,

то Fтр1= km1g, и тогда находим

T = F – km1g < km2g, Fтр2 =Т< km2g.

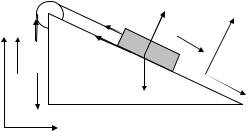
Задача 2.2. На наклонной плоскости, образующей угол α с горизонтом находится тело массы m1, соединенное невесомой нерастяжимой нитью с телом массы m2. Нить перекинута через невесомый блок. Трения в блоке нет. Коэффициент трения между телом и плоскостью равен k. Найти ускорение, с которым движутся тела.

Решение. Изобразим силы, действующие на тела, предполагая, что m1 опускается, а m2 поднимается (рис. 2.4). Тогда сила трения направлена навстречу движению тела m1, т.е. вверх вдоль плоскости.

Рис. 2.4

Так как нить невесома и нерастяжима, ускорения обоих тел одинаковы, а сила натяжения нити одинакова вдоль всей длины нити (см. задачу 2.1).

30

Вводя систему координат X1OY1 с осью ОХ1, направленной вниз параллельно плоскости, напишем уравнения второго закона Нью-

Уравнения (1)–(3) составляют систему трех уравнений для четырех неизвестных a, T, N, Fтр. Для получения однозначного решения требуется еще одно уравнение. Так как мы предполагаем, что тела движутся, то сила трения связана с нормальной компонентой силы реакции соотношением

Fтр = kN.

Это и есть четвёртое уравнение. Итак, имеем:

m1a = m1g sin α – T – kN, 0 = m1g cos α – N,

m2a = T – m2g.

Согласно второму уравнению системы

N = m1gcosα.

Подставляя найденное N в первое уравнение этой системы, и

Так как мы получили ответ, предполагая, что тела движутся в положительных направлениях осей ОХ1 и OY2, то а > 0, откуда

m1 (sinα – k cos α) > m2. (5)

Подчеркнем, что полученное неравенство – условие того, что m1 опускается.

Рассмотрим теперь обратный случай, когда m1 поднимается. Направления сил и координатных осей для этого случая изображены на рис. 2.5.

31

Опять, требуя а > 0, получим условие того, что m1 поднимается: m1 (sinα + k cos α) < m2.

то m1 не будет ни подниматься, ни опускаться, т.е. при выполнении условия (7) тела будут покоиться. Заметим еще, что неравенство (5)

Неравенство (8) – это условие того, что m1 вообще может опускаться. Если (8) нарушается, то даже при m2 = 0 тело m1 опускаться не будет, оно будет покоиться.

Задача 2.3. На гладком (трения нет) клине с углом наклона α, основание которого горизонтально, находится небольшое тело. С

32

каким ускорением в горизонтальном направлении следует перемещать клин, чтобы тело покоилось относительно клина?

Решение. Так как тело относительно клина покоится, а клин движется в горизонтальном направлении с ускорением а, то и тело движется вместе с клином с тем же ускорением в горизонтальном направлении. Согласно второму закону Ньютона

Здесь N – вся сила реакции клина, поскольку трение по условию отсутствует. Кроме силы тяжести mg и нормальной компоненты реакции опоры N на тело больше никакие силы не действуют. Выберем систему координат XOY с горизонтально направленной осью

ОХ (рис. 2.6).

a = g tg α.

Задача 2.4. На краю горизонтального диска радиуса R находится небольшое тело. Коэффициент трения между телом и диском равен k. Диск вращается с угловой скоростью ω. При каком значении ω тело соскользнет с диска?

Решение. Так как тело движется вместе с диском, то его траектория является окружностью радиуса R. Поскольку угловая скорость ω = const, то и скорость тела

υ = ω R = const,

и, следовательно, его тангенциальное ускорение

aτ = dυ/dt = 0.

Таким образом, ускорение a тела равно нормальному ускорению, которое всегда направлено к центру диска и равно

an = υ2 = ω2 R .

R

33

Рассмотрим силы, действующие на тело (рис. 2.7). Их две: сила тяжести mg и сила реакции диска R, которую мы, как всегда, представим в виде векторной суммы её нормальной компоненты и силы трения:

Так как тело покоится относительно диска, то Fтр – сила трения покоя и потому:

Fтр < kN.

Но N = mg, следовательно:

mω2R< k mg,

или

ω2< kg/R.

Если это условие выполняется, то тело по диску не скользит, если же нарушается, то начинается скольжение тела по диску. Итак, тело соскользнет с диска, если ω2 > kg/R.

Задача 2.5. Через невесомый блок, прикреплённый к потолку, перекинута невесомая нерастяжимая верёвка. К одному концу верёвки прикреплён груз массы m, а за другой конец ухватилась обезьяна такой же массы. Сначала система находится в покое, но в некоторый момент обезьяна начинает карабкаться вверх по верёвке. На какое расстояние относительно земли переместятся обезьяна и уравновешивающий её груз, если обезьяна переместилась по верёвке на расстояние L?

Решение. На обезьяну действуют две силы (рис. 2.8): тяжести и сила реакции верёвки. То же самое относится и к грузу. Если обо-

34

значить a1 и a2 ускорения соответственно обезьяны и груза, то для них можно записать уравнения второго закона Ньютона:

ma1 = T + mg, ma2 = T + mg.

Здесь учтено то обстоятельство, что невесомая верёвка действует с одинаковыми силами на соединённые с нею тела. Из написанных уравнений следует, что ускорения обезьяны и груза одинаковы. Следовательно, скорости и перемещения их также одинаковы. Пусть груз поднялся на высоту h. При этом противоположный конец верёвки опустился на высоту h. Обезьяна же, как и груз, поднялась относительно земли на ту же высоту h. Значит, она оказалась на

расстоянии 2h от своего конца верёвки. Но согласно Рис. 2.8 условию задачи это расстояние равно L, поэтому

L = 2h.

Откуда

h =L/2.

Задача 2.6. Через неподвижный блок перекинута верёвка, к одному из концов которой привязан груз массой m. С какой силой необходимо тянуть второй конец верёвки, чтобы груз начал подниматься? Коэффициент трения между верёвкой и поверхностью бло-

35

ляющая dN – силы реакции блока, dFтр – сила трения, Т и Т' – силы натяжения верёвки, приложенные к противоположным сторонам выделенного участка. Поскольку верёвка невесома, то сумма указанных сил равна нулю. Проецируя силы на направления касательной к блоку (ось X) и радиальное направление (ось Y), получим систему уравнений:

Обозначая dT = Т'– Т и учитывая, что сила трения скольжения

dFтр = kdN,

получим систему уравнений:

dN =Tdϕ, dT = kdN,

откуда dTT = kdϕ.

Интегрируя обе части этого уравнения, найдём lnT = kϕ +C.

Здесь С – постоянная интегрирования. Она находится из начальных условий: Т = mg при ϕ = 0. Отсюда находим С = ln(mg), и силу натяжения T = mg ekϕ .

Если верёвка накинута только сверху на блок, как это изображено на рис. 2.9, то сила натяжения на втором свободном конце верёвки согласно полученному результату равна (ϕ = π):

T = mg ekπ .

Если же верёвка обмотана вокруг блока n раз, то угол ϕ = = π + 2πn, откуда

T = mg ekπ(1+2n) .

Как видим, сила, необходимая для того, чтобы верёвка начала скользить по блоку, очень быстро возрастает с увеличением числа витков верёвки вокруг блока. Реально это означает, что, намотав даже небольшое число витков вокруг блока, вы не сможете сдвинуть верёвку с места, так велика будет необходимая для этого сила.

Задача 2.7. Материальная точка m находится внутри тонкого сферического слоя. Доказать, что сила тяготения, действующая на эту материальную точку со стороны слоя, равна нулю.

36

Решение. Для доказательства разобьём всю поверхность сферы на пары малых площадок так, чтобы каждая пара была образована

Здесь σ – масса сферического слоя, приходящаяся на единицу его площади.

Проведём из центра сферического слоя радиусы к площадкам dS1 и dS2. Треугольник, образованный этими радиусами и отрезок, соединяющий их концы, является равнобедренным. Пусть α – угол при основании этого треугольника. Спроецируем площадки dS1 и dS2 на направление перпендикулярное прямой, соединяющей эти площадки. Площади этих проекций, как нетрудно понять (рис. 2.10), равны

С другой стороны, согласно определению телесного угла, телесный угол dΩ, в пределах которого из точки т видны обе эти площадки, можно записать по-разному:

dΩ = dS1' = dS2' .

r12 r22

Полученное соотношение совместно с (1) и (2) показывает, силы dF1 и dF2 равны. Но это утверждение справедливо для каждой пары таких площадок, поэтому и весь сферический слой не оказывает никакого воздействия на материальную точку, находящуюся внутри него. Из полученного нами результата следует, что и слой конечной толщины также не оказывает никакого воздействия на

37

материальную точку, находящуюся внутри него, поскольку такой слой можно разбить на множество тонких слоёв, каждый из которых не действует на точку, находящуюся внутри него.

Задача 2.8. Оценить давление в центре Земли. Радиус Земли принять равным R=6400 км, а среднюю плотность Земли – ρ = = 5,5 103 кг/м3.

Решение. Выделим мысленно объём в виде слоя толщиной dr и площадью поперечного сечения S. Пусть эта частица находится на расстоянии r от центра Земли. Частица притягивается к центру Земли, поэтому, для того чтобы она находилась в равновесии, необходимо силу притяжения уравновесить разностью давлений:

зывает на частицу никакого влияния. Тогда сила притяжения легко находится. Действительно, если масса шара радиуса r равна М(r), то сила притяжения частицы массой dm к этому шару равна

Этот результат можно записать в более простом виде, если умножить и поделить его на куб радиуса Земли:

dF = G 43πρr dm = G 43π R3ρ Rr3 dm = G RM3 r dm = dm g Rr .

Здесь М – масса Земли, и кроме того, мы использовали то обстоятельство, что ускорение свободного падения на поверхности Земли можно записать как

g = G RM2 .

38

Уравнение (1) с учётом (2) приобретёт вид:

Подставляя сюда числовые параметры, найдём давление в центре Земли: р ≈ 1,8 1011 Па = 1,8 106 атм.

39