Астахов Електричество конспект лекций 2011

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ «МИФИ»

М. М. Астахов

ЭЛЕКТРИЧЕСТВО

КОНСПЕКТ ЛЕКЦИЙ

Для физико-математического лицея

Издание 4-е, с изменениями и дополнениями

Москва 2011

ТЕМА 1. ЭЛЕКТРОСТАТИКА

Электродинамика — раздел физики, в котором изучается электромагнитное взаимодействие тел и частиц.

Электромагнитное взаимодействие — один из видов фунда-

ментальных взаимодействий тел и частиц.

Электростатика — раздел электродинамики, в котором изучаются взаимодействие неподвижных (относительно какой-либо инерциальной системы отсчета) электрически заряженных тел и частиц.

§1. Электрический заряд

Электрический заряд q, Q — скалярная физическая величина (СФВ), определяющая силу и энергию электромагнитного взаимодействия тел и частиц.

Единица электрического заряда — кулон: [q] = Кл.

Кулон определяется через единицу силы тока — ампер (А):

Кл = А с (§14).

Свойства зарядов

1. Существуют два вида электрических зарядов: положительные, обозначаемые знаком плюс (+), и отрицательные, обозначаемые знаком минус (−).

Положительно заряженным становится, например, стеклянный стержень, потёртый о шёлк, отрицательно заряженным — янтарный стержень, потёртый о мех.

Между заряженными телами существует взаимодействие: одноимённо заряженные тела отталкиваются, разноимённо заряженные — притягиваются друг к другу.

2. Заряд любого тела является дискретным: он равен целому (либо положительному, либо отрицательному) числу N элементарных электрических зарядов:

Элементарный электрический заряд е — абсолютная величина наименьшего заряда:

3

Элементарным электрическим зарядом обладают, например, такие элементарные частицы, как протон, являющийся положительно заряженной частицей (qпр = е), и электрон, являющийся отрицательно заряженной частицей (qэл = −е).

3. Электрический заряд тела не зависит от скорости тела. Заряд тела во всех инерциальных системах отсчета одинаков.

Электрический заряд в дальнейшем будет называться (для краткости) зарядом.

Электризация тел — образование на теле избытка (недостатка) положительного или отрицательного заряда.

При электризации двух разнородных тел, например соприкосновением (в частности, при трении тел друг о друга), оба тела приобретают заряды разных знаков, но одинаковые по абсолютной величине (вследствие того, что некоторое количество электронов переходит с тела, диэлектрическая проницаемость (§5) которого больше, на другое, соприкасающееся с ним, тело).

Заряженное (наэлектризованное) тело — тело с избытком

(недостатком) положительного или отрицательного заряда.

Положительно заряженное тело — заряженное тело с избыт-

ком положительного (недостатком отрицательного) заряда.

Отрицательно заряженное тело — заряженное тело с избыт-

ком отрицательного (недостатком положительного) заряда.

Электрически нейтральное тело — тело, заряд которого равен нулю (вследствие того, что общий положительный и общий отрицательный заряды частиц тела равны по абсолютной величине).

Заряд системы тел qc равен сумме зарядов qi тел данной системы:

i=1

где n — число заряженных тел системы.

Изолированная система тел — система тел, которая не может обмениваться заряженными телами (или заряженными частицами) с внешней средой.

4

Закон сохранения электрического заряда

Заряд изолированной системы тел при любых процессах, происходящих в данной системе, остается постоянным:

Заряженные тела и частицы в дальнейшем будут называться (для краткости) зарядами.

§2. Закон Кулона

Точечный заряд — заряженное тело, размерами которого можно пренебречь в данной задаче.

Закон Кулона

Силы, с которыми действуют друг на друга два неподвижных точечных заряда, направлены по прямой, проходящей через эти заряды, равны по величине и противоположны по направлению. Эти силы являются силами отталкивания, если заряды одноимён-

ные, и силами притяжения, если заряды разноимённые. Величина сил прямо пропорциональна произведению модулей этих зарядов и обратно пропорциональна квадрату расстояния между ними.

Точечные заряды (при использовании в законе Кулона) — заряженные тела, максимальный линейный размер Li max которых много меньше минимального расстояния rmin между ними:

Li max << rmin (i = 1,2; rmin — наименьшее из расстояний между любыми двумя точками заряженных тел).

Закон Кулона в векторной форме

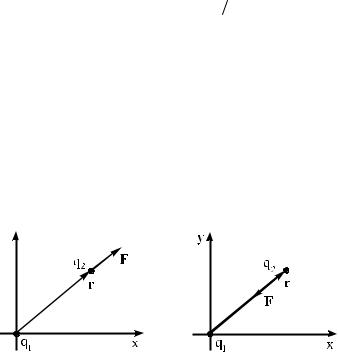
Пусть точечный заряд q1 находится в начале координат xOy (рис.2.1), точечный заряд q2 находится в точке, радиус-вектор которой r.

Если заряды находятся в вакууме (газовой среде при давлении много меньше атмосферного), на заряд q2 действует заряд q1 с силой F2,1 (кулоновской силой), которая может быть представлена в виде выражения:

5

где кэл — коэффициент пропорциональности, определяемый (в СИ) равенством:

ε0 — электрическая постоянная:

с — скорость света в вакууме (с = 3·108 м/с), Ф (фарад) — единица электрической емкости (§6).

Сила F2,1 является:

а) силой отталкивания, если оба заряда q1 и q2 имеют одинаковые знаки (сила F2,1 направлена по радиус-вектору r от заряда q1 —

рис.2.1,а);

б) силой притяжения, если оба заряда q1 и q2 имеют разные знаки (сила F2,1 направлена противоположно радиус-вектору r к заряду q1 — рис.2.1,б).

Модуль кулоновской силы

Если заряды находятся в однородной и изотропной (свойства одинаковы по всем направлениям) бесконечной диэлектрической среде, кулоновская сила уменьшается в ε раз по сравнению с силой

6

в вакууме:

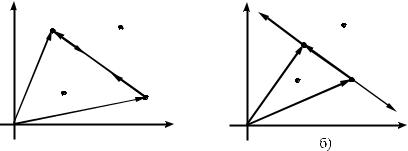
где ε — относительная диэлектрическая проницаемость среды (§5). В общем случае, когда ни один из зарядов не находится в начале координат, кулоновские силы, с которыми действуют друг на друга точечные заряды (на рис.2.2,а — заряды разноименные, на рис.2.2,б — заряды одноименные), могут быть представлены в виде

выражения:

где Fi,j — кулоновская сила, с которой j-й заряд действует на i-й заряд (i,j = 1,2,…n; i ≠ j); ri,j — вектор, начало которого находится на j-м заряде, конец вектора — на i-м заряде:

где ri и rj — радиус-векторы точечных зарядовqi и qj соответственно.

Из формулы (2.6) следует, что i-й и j-й заряды действуют друг на друга силами, равными по модулю, лежащими на прямой, проходящей через оба заряда, и направленными в противоположные стороны:

7

Формула (2.6) может быть использована для определения сил и при движении точечных зарядов, если модуль их относительной скорости значительно меньше скорости света в вакууме (vотн << с).

Принцип независимости действия (суперпозиции) сил

Если на i-й заряд системы точечных зарядов действуют одновременно несколько зарядов, то равнодействующая сила, приложенная к этому заряду

частиц значительно превосходят силы их гравитационного взаимодействия. Например, при взаимодействии двух электронов (масса электрона mэл = 9,1 10−31кг) кулоновские силы больше (по модулю)

гравитационных в 4,2 1042 раз, двух протонов (масса протона mпр = 1,67 10−27кг) — в 1,2 1036 раз.

§3. Напряжённость электростатического поля

Электромагнитное поле — поле, посредством которого осуществляется электромагнитное взаимодействие тел и частиц.

Электростатическое поле — поле, создаваемое неподвижными (в какой-либо инерциальной системе отсчёта) зарядами.

На заряд, находящийся в электростатическом поле, действует сила, определяемая напряженностью этого поля.

Электростатическое поле в дальнейшем будет называться (для краткости) полем.

Напряженность поля (в некоторой точке) Е — векторная физическая величина (ВФВ), равная отношению кулоновской силы Fкл, действующей на пробный заряд q, находящийся в этой точке поля, к этому заряду:

8

Напряженность поля в некоторой точке совпадает по направлению с кулоновской силой, действующей на положительный пробный заряд, находящийся в этой точке.

Пробный заряд — точечный заряд, используемый для определения характеристик электрического поля.

Величина пробного заряда должна быть достаточно малой, чтобы практически не изменять распределения тех зарядов, которые создают исследуемое поле.

Единица напряженности поля — вольт на метр: [E] = В/м (вольт — единица потенциала, §4).

Напряженность поля точечного заряда

Пусть точечный заряд q находится (в вакууме) в начале коор-

динат xOy (рис.3.1).

Точечный заряд (при определении напряженности поля) — заряд, максимальный размер L max которого значительно меньше, чем расстояние r от него до тех точек, в которых определяются напряженность поля (L max << r).

Напряженность поля E точечного заряда q в точке, радиусвектор которой r:

где кэл — коэффициент пропорциональности, определяемый равен-

ством (2.2).

Поле точечного заряда является центральным. Напряженность поля положительного точечного заряда направлена от заряда (на

9

рис.3.1,а показана напряженность в точке С), отрицательного — к заряду (на рис.3.1,б показана напряженность в точке D).

Модуль напряженности поля точечного заряда q:

где r — модуль радиус-вектора данной точки.

Принцип суперпозиции полей

Напряженность поля системы точечных зарядов Eс в некоторой точке равна сумме напряженностей полей Ei, создаваемых каждым зарядом qi данной системы в этой точке по отдельности:

i=1

где n — число зарядов в системе.

Электрический диполь — система, состоящая из двух одинаковых по абсолютной величине разноименных точечных зарядов.

Ось диполя — прямая, проходящая через оба заряда.

Электрический момент диполя P — ВФВ, определяемая про-

изведением:

где q — положительный заряд; l — вектор, начало которого находится на отрицательном заряде, конец — на положительном заряде диполя (рис.3.2).

Электрический точечный диполь — диполь, расстояние между зарядами которого значительно меньше, чем расстояние до тех точек, в которых определяется напряженность поля этих зарядов.

Напряженность поля Eo на оси точечного диполя в точке, ра- диус-вектор которой ro (начало координат xOy находится в центре диполя, см. рис.3.2):

Напряженность поля Eп точечного диполя на прямой, перпен-

10