Математика Лабораторный практикум часть 2

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Южно-Российский государственный университет экономики и сервиса» (ФГБОУ ВПО «ЮРГУЭС»)

МАТЕМАТИКА

Лабораторный практикум

для самостоятельной работы студентов 2 курса очной, заочной и дистанционной форм

обучения всех направлений и специальностей

В 2 частях

Часть 2

ШАХТЫ ФГБОУ ВПО «ЮРГУЭС»

2012

УДК 519.2(076.5) ББК 22.171я73

М34

Рекомендован к внутривузовскому изданию редакционно-издательским советом ЮРГУЭС

Издание выходит с 2011 г.

Составители:

к.ф.-м.н., доцент кафедры «Математика» ЮРГУЭС

А.Б. Михайлов

к.т.н., доцент кафедры «Математика» ЮРГУЭС

Г.Р. Саакян

к.т.н., доцент кафедры «Математика» ЮРГУЭС

И.Д. Михайлова

к.ф.-м.н, доцент кафедры «Математика» ЮРГУЭС

К.А. Михайлов

старший преподаватель кафедры «Математика» ЮРГУЭС

С.В. Рубцова

Рецензенты:

к.э.н., доцент кафедры «Математика» ЮРГУЭС

О.И. Охрименко

к.т.н., доцент кафедры «Математика» ЮРГУЭС

О.А. Алейникова

М34 Математика: лабораторный практикум: в 2 ч. / составители А.Б. Михайлов, Г.Р. Саакян, И.Д. Михайлова, К.А. Михайлов, С.В. Рубцова. – Шахты : ФГБОУ ВПО «ЮРГУЭС», 2011–2012.

Ч. 2. – 89 с.

Лабораторный практикум содержит варианты заданий по лабораторным работам, выполняемым по разделу математики «Теория вероятностей и математическая статистика», примеры их выполнения, краткий справочный материал, а также контрольные вопросы для защиты лабораторных работ.

Лабораторный практикум предназначен в помощь студентам 2 курса очной, заочной и дистанционной форм обучения для подготовки и выполнения лабораторных работ по курсу высшей математики.

УДК 519.2(076.5) ББК 22.171я73

Режим доступа к электронному аналогу печатного издания: http://www.libdb.sssu.ru

©ФГБОУ ВПО «Южно-Российский государственный университет экономики и сервиса», 2012

2

СОДЕРЖАНИЕ

3

ПРЕДИСЛОВИЕ

Методы теории вероятностей широко применяются в различных отраслях естествознания и техники: в теории надёжности, теории массового обслуживания, в теоретической физике, теории ошибок наблюдений, теории автоматического управления и во многих других теоретических и прикладных науках. Теория вероятностей служит также для обоснования математической и прикладной статистики, которая, в свою очередь, используется при планировании и организации производства, при анализе технологических процессов, предупредительном и приёмочном контроле качества продукции и для многих других целей. В последние годы методы теории вероятностей всё шире и шире проникают в различные области науки и техники, способствуя их прогрессу.

В данном лабораторном практикуме предлагается курс лабораторных работ, основная задача которых состоит в обучении студентов методам решения задач по теории вероятностей и математической статистики с помощью ЭВМ. Лабораторный практикум включает в себя пять лабораторных работ по основным темам, предусмотренным учебной программой по дисциплине «Теория вероятностей и математическая статистика». Лабораторные работы выполняются с привлечением математического пакета Maple.

Практикум имеет следующую структуру:

лабораторные работы по разделам теории вероятностей и математической статистике, включающие последовательное описание их выполнения;

краткий теоретический материал;

варианты, предлагаемые студентам для самостоятельного выполнения;

контрольные вопросы для защиты лабораторных работ. Студент должен выполнить свой вариант лабораторной работы

иоформить отчёт по ней. Отчёт должен содержать:

название лабораторной работы;

цель работы;

задание своего варианта;

результаты решения на ЭВМ;

анализ полученного решения, интерпретацию результатов;

выводы.

Настоящее пособие позволит студентам понять, как применять математическую теорию на практике.

4

Лабораторная работа 1 Схема Бернулли

Цель работы: научиться пользоваться формулами Бернулли, Пуассона, локальной и интегральной теоремами Муавра – Лапласа, по условию задачи правильно выбирать и применять для решения нужную формулу.

Краткий теоретический материал. Схема Бернулли состоит в следующем: проводится n независимых испытаний, в каждом испытании вероятность появления некоторого события A одна и та же и равна p. Вероятность того, что в n независимых испытаниях событие A наступит ровно m раз, определяется по формуле Бернулли:

формуле Бернулли превращается в технически сложную задачу. По-

Pn(m) me , где np. m!

Значения функции me приведены в таблице приложения 3. m!

Если требуется найти вероятность того, что событие A наступит не менее m1 и не более m2 раз, то при больших n и при p 0;1можно воспользоваться интегральной теоремой Муавра – Лапласа:

5

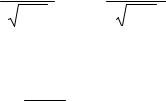
x1 m1 np, x2 m2 np . npq npq

Функция (x) нечётная, её значения приведены в таблице приложения 2. Также для этой цели можно использовать формулу

m2 ie

Пуассона: Pn(m1 k m2) , np.

i m1 i!

Задание. Решить задачи 1, 2, 3, применяя формулы Бернулли, Пуассона, локальную и интегральную теоремы Муавра – Лапласа. Расчёты вероятности в каждой задаче провести с использованием пакета прикладных программ Maple. Сравнить результаты, сделать выводы.

Варианты заданий Задача 1 (m номер варианта).

Варианты 1–5. Вероятность того, что деталь при проверке окажется бракованной, равна 0,05. Найти вероятности того, что среди проверенных десяти деталей:

а) ровно m окажутся бракованными;

б) не более m 1 окажутся бракованными; в) не менее m 2 окажутся бракованными.

Варианты 6 – 10. Вероятность попадания при каждом из 12 выстрелов равна 0,75. Найти вероятности того, что мишень будет поражена:

а) ровно m раз; б) не более m раз;

в) не менее m 1 раза.

Варианты 11–15. Вероятность того, что лотерейный билет будет выигрышным, считается постоянной и равной 0,02. Найти вероятности того, что среди 9 купленных билетов:

а) ровно m 10 окажутся выигрышными; б) не более m 9 окажутся выигрышными; в) не менее m 8 окажутся выигрышными.

Варианты 16–20. Найти вероятности того, что при 11 бросаниях игральной кости шестёрка выпадет:

а) ровно m 14 раз; б) не более m 13 раз; в) не менее m 12 раз.

Варианты 21–25. Вероятность того, что зашедший в магазин человек сделает покупку, равна 0,42. Найти вероятность того, что из 15 человек покупку сделают:

а) ровно m 17 человек; б) не более m 15 человек; в) не менее m 14 человек.

6

Задача 2 (m номер варианта). При перевозке стеклотары вероятность боя одной бутылки равна 0,002. Найти вероятности того, что при перевозке 1000 10m бутылок будет разбито:

а) ровно 3 бутылки; б) не более 3 бутылок;

в) не менее 3 и не более 3 mбутылок.

Задача 3 (m номер варианта). Вероятность всхода семян данного растения равна 0,85. Найти вероятности того, что при посадке 500 10m семян взойдёт:

а) ровно 450 3m растений; б) не менее 400 растений;

в) не менее 420 и не более 420 5m растений.

Пример выполнения лабораторной работы

Задача 1. Вероятности выигрыша по облигациям займа равна 0,25. Какова вероятность того, что из 8 взятых облигаций:

а) выиграют ровно 3; б) выиграют не более 3; в) выиграют не менее 4.

Решение. а) Так как число облигаций, участвующих в розыгрыше, невелико, воспользуемся формулой Бернулли для решения задачи:

> restart: n:=8;m:=3;p:=0.25;

Проводим вычисления.

> P(n,k<=m,p):=sum(n!/(i!*(n-i)!)*p^i*(1-p)^(n-i),i=0..3);

P(8,k≤ 3,0.25)=0.8861846924

в) Вероятность события «выиграют не менее 4» находим как вероятность противоположного события к событию «выиграют не более 3»:

>P(n,k>=m+1,p):=1 – P(n,k<=m,p);

P(8,4≤ k,0.25)=0.1138153076

7

Задача 2. Обувной магазин продал 200 пар обуви. Вероятность того, что в магазин будет возвращена бракованная пара, равна 0,01. Найти вероятность того, что из проданных пар обуви будет возвращено:

а) ровно 4 пары; б) не более 4 пар;

в) не менее 3 и не более 8 пар.

Решение. Найдём точное значение вероятности в задаче а) по формуле Бернулли и приближённые значения вероятности с помощью формулы Пуассона и локальной теоремы Муавра – Лапласа. Имеем

> restart: n:=200;m:=4;p:=0.01; n:=200 m:=4 p:=0.01

По формуле Бернулли:

> P(n,m,p):=n!/(m!*(n-m)!)*p^m*(1-p)^(n-m);

P(200,4,0.01):=0.09021970194

По формуле Пуассона:

> P1(n,m,p):=evalf((n*p)^m*exp(-n*p)/m!);

P1(200,4,0.01):= 0.09022352212

С использованием локальной теоремы Муавра – Лапласа:

> x:=(m-n*p)/sqrt(n*p*(1-p)); x:=1.421338109

> P(n,p,x):=evalf(1/sqrt(n*p*(1-p))*(1/sqrt(2*Pi))*exp(-x^2/2));

P(200,4, 1.421338109):=0.1032514539

Делаем вывод о том, что более точный результат даёт формула Пуассона.

Замечание. При больших n и при малых значениях p 0,1 более точный результат даёт формула Пуассона, поэтому задачи б) и в) будем решать с использованием этой формулы.

б) Находим искомую вероятность по формуле:

4

P(200,k 4,0.01) (np)i e np /i!

i 0

>P(n,k<=4,p):=evalf(sum((n*p)^i*exp(-n*p)/i!,i=0..4));

P(200,k≤ 4,0.01):= 0.9473469824

в) Найдём вероятность того, что из проданных пар обуви будет возвращено не менее 3 и не более 8 пар. Воспользуемся вновь форму-

8

лой Пуассона: P(200,3 k 8,0.01) (np)i e np /i!

i3

>P(n,3<=k,k<=8,p):=evalf(sum((n*p)^i*exp(-n*p)/i!,i=3..8));

P(200, 3<=k,k<=8, 0,01):= 0.05241557000

8

Задача 3. Вероятность того, что случайный покупатель потратит в супермаркете более 500 руб., равна 0,24. Найти вероятность, что из 400 покупателей более 500 руб. потратят:

а) ровно 100 чел.; б) не более 100 чел.;

в) не менее 85 и не более 125 чел.; Решение. Найдём точное значение вероятности в задаче а) по

формуле Бернулли и приближённые значения вероятности с помощью формулы Пуассона и локальной теоремы Муавра – Лапласа. Имеем

> restart: n:=400;m:=100;p:=0.24; n:=400 m:=100 p:=0.24

По формуле Бернулли:

> P(n,m,p):=n!/(m!*(n-m)!)*p^m*(1-p)^(n-m);

P(400,100,0.24):= 0.04128662045

По формуле Пуассона:

> P1(n,m,p):=evalf((n*p)^m*exp(-n*p)/m!);

P1(400,100,0.24):= 0.03671549490

Локальная теорема Муавра – Лапласа:

> x:=(m-n*p)/sqrt(n*p*(1-p));

x:=0 .4682929058

> P(n,p,x):=evalf(1/sqrt(n*p*(1-p))*(1/sqrt(2*Pi))*exp(-x^2/2));

P(400,100,0 .4682929058):= 0.04185502868

Делаем вывод о том, что в данной ситуации более точный результат даёт локальная теорема Муавра – Лапласа, поэтому задачи б) и в) будем решать с использованием интегральной теоремы Муавра – Лапласа.

б) Имеем

> m1:=0;m2:=100;

m1:=0

m2:=100

> x1:=(m1-n*p)/sqrt(n*p*(1-p)); x2:=(m2-n*p)/sqrt(n*p*(1-p)); x1:= -11.23902974

x2:= 0.4682929058

> P(n,m1<=k,k<=m2,p):=evalf(1/sqrt(2*Pi)*int(exp(-x^2/2),x=x1..x2));

P(400, 0≤k≤100, 0.24)=0 .6802124294

в) Найдём вероятность, что из 400 покупателей более 500 руб. потратят не менее 85 и не более 125 чел.

> m1:=85;m2:=125;

m1:=85

m2:=125

> P(n,m1<=k,k<=m2,p):=evalf(1/sqrt(2*Pi)*int(exp(-x^2/2),x=x1..x2));

P(400,85≤k≤125,0.24)=0 .9007501711

9

Контрольные вопросы

1.Какие испытания называются независимыми? Приведите примеры независимых испытаний.

2.Что понимают под схемой Бернулли? Приведите примеры ситуаций, в которых присутствует схема Бернулли.

3.Что такое «успех» и «неудача» в схеме Бернулли? Как связаны их вероятности?

4.Запишите формулу Бернулли. Какую вероятность вычисляют по этой формуле? Приведите примеры задач, в которых используется формула Бернулли.

5.В каких случаях и какие приближённые формулы используют в схеме Бернулли ?

6.При каких условиях более точный результат даёт та или иная приближённая формула?

7.Приведите примеры задач, в которых используются формула Пуассона и локальная теорема Муавра – Лапласа.

8.Как найти вероятность того, что в п испытаниях схемы Бернулли «успех» наступит: а) не более m раз; б) более m раз; в) не менее m раз; г) менее m раз.

9.Сформулируйте интегральную теорему Муавра – Лапласа. Приведите примеры задач, в которых используется эта теорема.

10. Каким образом нужно решать следующую задачу: найти вероятность того, что в 450 независимых испытаниях «успех» наступит не менее 10 и не более 15 раз, если вероятность «успеха» в каждом испытании равна 0,3 (если вероятность «успеха» в каждом испытании равна 0,03).

Лабораторная работа 2 Исследование дискретной и непрерывной случайных величин

Цель работы: научиться использовать закон распределения случайной величины для нахождения вероятностей и числовых характеристик исследуемой случайной величины.

Краткий теоретический материал. Случайной величиной (с.в.)

называется величина, которая в результате опыта со случайным исходом принимает то или иное значение. Случайная величина называется дискретной (д.с.в.), если множество её значений конечно или счётно. Случайная величина называется непрерывной, если множество её значений занимает некоторый промежуток.

10