Зависимость величины ошибки от измеряемого значения
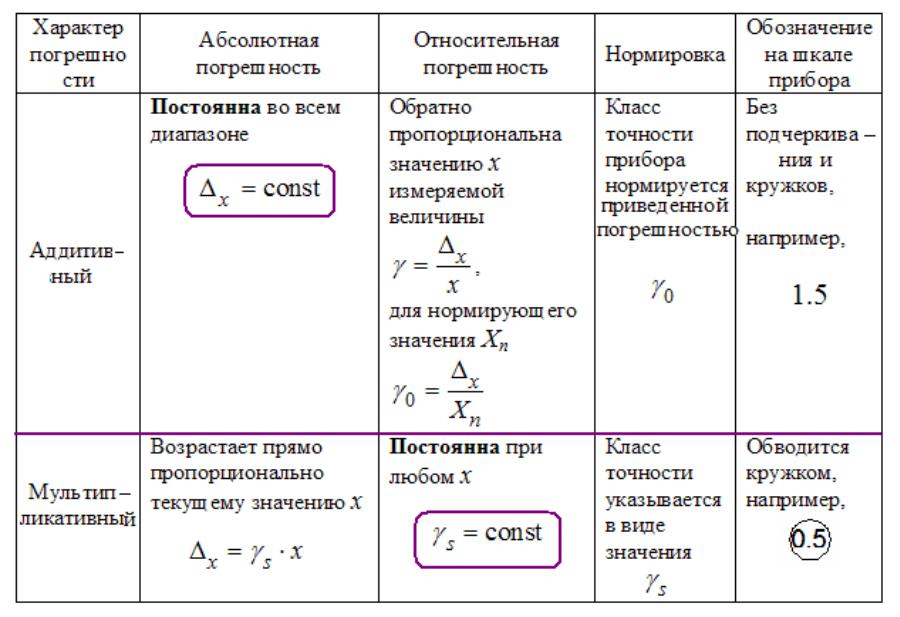
•Величина ошибок, получающихся в процессе измерения, зависит от значения измеряемой величины.
•В зависимости от природы той или иной ошибки эта связь может быть различной.
ПРИМЕРЫ:
•Пример 1. Линейка (деревянная) после изготовления и нанесения делений удлинилась (вследствие набухания). При этом относительная ошибка любого измерения равна относительному удлинению линейки. =const
•Пример 2. Цена первого деления линейки больше других на L. При отсчете от начала шкалы абсолютная погрешность любого измерения будет равна L. x=const
Способы уменьшения систематических ошибок
•При производстве измерений 1 из основных забот д.б. забота об учете и исключении систематических ошибок, которые в ряде случаев могут заметно искажать результаты измерений.
Путь 1. Ошибки, природа которых нам известна и величина может быть достаточно точно определена, устраняются введением соответствующих поправок.
Пример. Измерение с помощью стальной линейки (изготовленной при 00С) диаметра латунного цилиндра, измерение проводится при 250С.
•Величина поправок, которые еще есть смысл вводить, разумеется устанавливаются в зависимости от величин других ошибок, сопровождающих измерение.
•Правило: если поправка не превышает 0.005 от средней квадратичной ошибки результата измерений, то ею следует пренебречь.
Замечание. Обычно можно пренебречь и большими поправками.
Способы уменьшения систематических ошибок
Путь 2. Ошибки известного происхождения, но неизвестной величины (например, погрешность прибора, определяемая классом точности), не могут быть исключены, но их наибольшее значение, как правило, известно.
Путь 3. Ошибки, о существовании которых мы не подозреваем, хотя величина их может быть очень значительна. Имеют место чаще при сложных измерениях.
Пример. Измерение плотности металла через определение объема и веса образца.
Если образец содержит внутри пустоту, то мы совершим грубую ошибку!
Вывод: при более сложных и важных измерениях необходимо тщательно продумывать их методику.
Еще один путь борьбы с систематическими ошибками
•В ряде случаев систематическая ошибка может быть переведена в
случайную. Этот прием называется
рандомизацией.
Пример. Многократное взвешивание с использованием гирь из различных наборов.
Необходимость учета случайных ошибок
•Допустим, что все систематические ошибки у нас учтены:
1)поправки, которые следовало определить вычислены;
2)Класс точности измерительного прибора известен;
3)Есть уверенность, что отсутствуют какие-либо существенные и неизвестные нам источники систематических ошибок
В этом случае результаты измерений все же несвободны от случайных ошибок.
Соотношение систематической и случайной погрешностей
•Если СЛО<ССО, то нет смысла еще уменьшать СЛО – все равно результаты измерений не станут от этого заметно точнее. Для повышения точности надо искать пути к уменьшению систематической ошибки.
•Если СЛО>ССО, то именно случайную ошибку нужно уменьшать в первую очередь: проводить не 1, а ряд измерений.
ПРАВИЛА:
•1. Если ССО является определяющей, т.е. ее величина существенно больше величины СЛО. Присущей данному методу, то достаточно выполнить измерение 1 раз.
•2. Если СЛО является определяющей, то измерение следует проводить несколько раз. Число измерений целесообразно выбирать таким, чтобы СЛО среднего арифметического была меньше ССО, с тем, чтобы последняя опять определила окончательную ошибку результата.
Вывод: Необходимое число измерений определяется в конечном итоге соотношением величин ССО и СЛО.
Определение вероятности
•Пусть в урне n белых и m черных шаров.
•При изъятии наугад шара из урны для какого цвета шансов больше????
•Отношение числа белых шаров к общему числу шаров в урне носит название вероятности появления белого шара.
P(n) |
n |
|
n m |
||
|
P(m) m n m
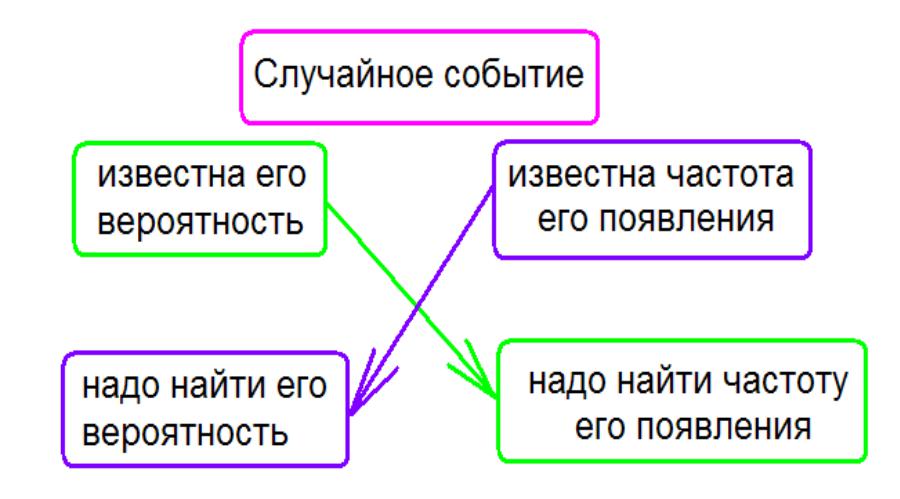
Прямая и обратная задачи
Как найти вероятность?
• Опытным путем с достаточно хорошим приближением вероятность неизвестного нам случайного события устанавливается на основе
соотношения: k
P(m) N
ВЫВОД: Частота появления случайного события определяется его вероятностью.
Можно назвать практически достоверными события, вероятность которых отличается от единицы на 10-6 — 10-7, а практически невозможными те, вероятность которых меньше 10-6 — 10-7.