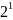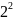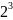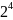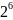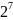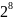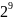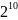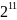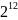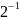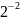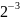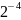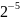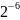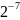1.3. Преобразование чисел в различные системы счисления

Для практической деятельности актуальна задача преобразования чисел представленных в одной системе счисления в другую. Задача состоит в представлении числа в требуемой СС с основанием q_тр, если оно задано в исходной системы СС с основанием q_исх.

Для преобразования могут использоваться следующие методы:

- Метод подбора;

- схема Горнера;

- метод «цифра за цифрой»;

- специфическое соотношение оснований;

- через промежуточную систему счисления.

Ниже подробно будут рассмотрены методы перевода чисел из одной системы счисления в другую метод подбора, «цифра за цифрой» и метод, основанный на специфическом соотношений оснований.

Метод подбора.

Метод используется для преобразований “в уме”. Служит в основном для преобразований из десятичной в двоичную систему счисления. Метод описывается следующим алгоритмом.

Алгоритм.

1. Подбирается ближайшая снизу к заданному числу (текущему остатку) степень двойки, не превосходящая числа (остатка). В соответствующей позиции двоичного числа записывается единица. Промежуточные старшие позиции заполняются нулями.

2. Определяется разность между числом (текущим остатком) и значением подобранной степени. Разность наз. текущим остатком.

3. Если разность не равна 0 или не отрицательно, то переход на п.1.

Иначе: конец.

Конец

Процедура интуитивно понятна, требует знания степеней двойки. Выполняется в десятичной арифметике. Теоретически возможно использование метода для преобразования в другие системы счисления. Однако в системах отличных от двоичных, требуется в качестве вычитаемых из текущего остатка использовать не только значения степени недвоичных оснований, а их произведения на соответствующие цифры. В этом случае подбирается не только ближайшая степень основания требуемой системы счисления, но и соответствующая цифра. Поэтому для таких “ручных” преобразований метод сложен, поэтому не применяется.

В таблицах 3, 4 приведены значения некоторых степеней двойки

Таблица 3 – Степени двойки для преобразования целого числа

Степень
Десятичный эквивалент	2	4	8	16	32	64	128	256	512	1024	2048	4096

Таблица 4 – Степени двойки для преобразования дробного числа

Степень
Десятичный эквивалент	0,5	0,25	0,125	0,0625	0,0 3125	0,015625	0,0078125

Пример. Перевести число 47D в двоичную систему счисления методом подбора.

47D = 32 + 8 + 4 + 2 +1 = 2⁵ + 2³ +2² + 2¹ + 2⁰ = 101111B

Метод «цифра за цифрой».

Метод “цифра за цифрой” предусматривает последовательное получение цифр кода числа.

При этом для целого числа, а равно для целой части смешанного числа преобразование выполняется с использованием операции деления, а для дробного числа (дробной части смешанного числа) с использованием операции умножения. Преобразование для каждой части имеет свои особенности, поэтому соответствующие алгоритмы целесообразно рассмотреть отдельно.

Перевод целых чисел.

Чтобы перевести целое число из одной позиционной СС в другую, его надо последовательно делить на основание новой СС до тех пор, пока остаток не станет меньше делителя. Число в новой СС записывается из остатков от последовательного деления, причем последний остаток будет старшей цифрой нового числа.

П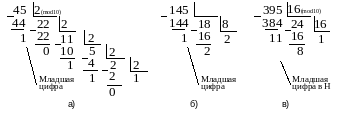 ример . Выполнить, используя метод “цифра за цифрой”, перевод целых десятичных чисел 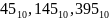, соответственно, в двоичную, восьмеричную и шестнадцатеричную системы счисления.

Перевод правильных дробей.

Для перевода правильных дробей необходимо исходную дробь умножить на основание СС до тех пор, пока в новой дроби не будет нужного количества цифр, которое определяется требуемой точностью вычислений.

Пример. Преобразовать десятичное число 0,375D в двоичную систему счисления.

0 .375 D В 0.375D = 0.011В

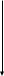0. 375

х 2

0. 750

х 2

1. 500

х 2

1. 000

При преобразовании смешанного числа его целая и дробная часть преобразуются соответственно методами “деления лесенкой“ и “последовательного умножения“. Далее из полученных целого и дробного чисел в новой системе счисления составляется (конкетенация) преобразованное смешанное число. Целая и дробная часть числа разделяются запятой.

Метод, основанный на специфическом соотношении основании систем счисления.

Практический интерес представляют взаимные преобразования в двоичной, восьмеричной и шестнадцатеричной системах счислениях, поскольку базисы 8 и 16 являются степенями базиса 2.

Перевод смешанного 8-ричного числа в двоичную СС

1.Каждая цифра восьменричного числа заменяется соответствующей по количественному эквиваленту двоичной триадой.

2.Незначащие старшие и младшие нулевые разряды соответственно в целой и дробной части двоичного числа для “ вписывания ” в заданную разрядную сетку могут быть отброшены.

3.Положение запятой и знак числа – сохраняются.

При переводе можно воспользоваться данными таблицы 5

Таблица 5– Соответствие “триада-цифра”

000	001	010	011	100	101	110	111
0	1	2	3	4	5	6	7

Пример. Преобразовать восьмеричное число 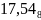в двоичную систему счисления.

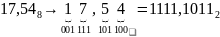
Обратное преобразование основано на том же соотношении систем счисления.

Преобразование смешанного двоичного числа в числа в восьмеричную систему счисления

1. Двоичное число разбивается на группы из трех разрядов (триады). Если в старшей триаде менее чем три цифры, то вместо отсутствующих цифр записывают нули, которые дополняют триаду до полной.

2.Если в младшей триаде менее чем три цифры, то она дополняется справа нулями до полной триады

3.Комбинация цифр в каждой триаде рассматривается как целое число, которое заменяется соответствующей восьмеричной цифрой.

4.Полученное число – число в восьмеричной системе счисления.

Пример. Преобразовать в восьмеричную систему смешанное двоичное число 110110,1110110₂.

Целая часть:

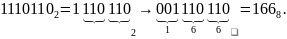
Дробная часть:

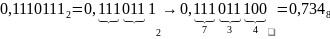
Итог преобразования: 166,734₈.

Преобразование смешанного двоичного числа в шестнадцатеричную систему счисления

1.Каждая цифра шестнадцатеричного числа заменяется соответствующей по количественному эквиваленту двоичной тетрадой.

2.Незначащие старшие и младшие нулевые разряды соответственно в целой и дробной части двоичного числа для “ вписывания ” в заданную разрядную сетку могут быть отброшены.

3.Положение запятой и знак числа – сохраняются.

При преобразовании можно воспользоваться данными таблицы 6.

Таблица 6 – Соответствие “ цифра-тетрада”

0	1	2	3	4	5	6	7
0000	0001	0010	0011	0100	0101	0110	0111

Таблица 3.5 (продолжение)

8	9	A	B	C	D	E	F
1000	1001	1010	1011	1100	1101	1110	1111

Пример. Перевести смешанное шестнадцатеричное число в двоичную систему счисления.

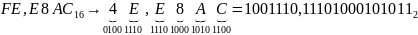
Обратное преобразование основано на том же соотношении систем счисления.

Пример. Перевести дробное двоичное число в шестнадцатеричную систему счисления.

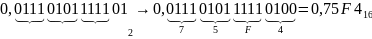
Младшая неполная тетрада исходного двоичного дробного числа дополнена до полной нулями, затем произведены замены тетрад по количественным эквивалентам.

1.4. Формы представления данных

В ЭВМ используются следующие формы представления данных:

- числа с фиксированной точкой (запятой);

- числа с плавающей точкой (запятой);

- десятичные числа;

- символьные данные.

При представлении числа X в форме с фиксированной точкой указываются знак числа (sign X) и модуль числа (mod X) в q-ичном коде. Иногда такую форму представления чисел называют естественной формой. Место точки (запятой) постоянно для всех чисел и в процессе решения задач не меняется. Знак положительного числа кодируется цифрой "0", а знак отрицательного числа – цифрой "1".

Код числа в форме с фиксированной точкой, состоящий из кода знака и q-ичного кода его модуля, называется прямым кодом q-ичного числа. Разряд прямого кода числа, в котором располагается код знака, называется знаковым разрядом кода. Разряды прямого кода числа, в которых располагается q-ичный код модуля числа, называются цифровыми разрядами кода. При записи прямого кода знаковый разряд располагается левее старшего цифрового разряда и обычно отделяется от цифровых разрядов точкой.

В общем случае разрядная сетка ЭВМ для размещения чисел в форме с фиксированной точкой показана на рис. (3.4,а). На рисунке показано n разрядов для представления целой части числа и m разрядов для – дробной части числа.

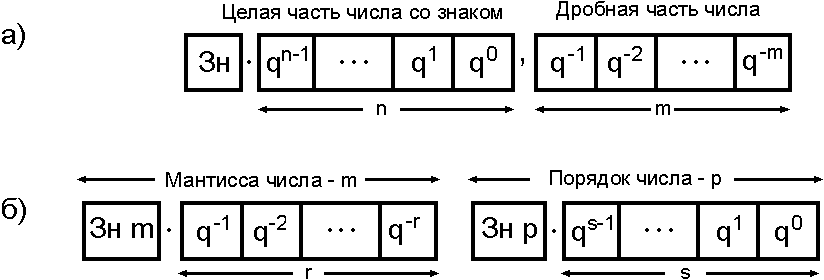
Рис.2. Формы представления чисел в ЭВМ

При заданных n и m диапазон изменения модулей чисел, коды которых могут быть представлены в данной разрядной сетке, определяется неравенством

q^-m £ ïXï £ qⁿ – q^-m (1.11)

Для двоичной системы счисления это

2^-m £ ïXï £ 2ⁿ – 2^-m (1.12)

Соответственно максимальное и минимальное значения чисел определяются формулами:

X_max = +(qⁿ – q^-m) (1.13)

X_min = -(qⁿ – q^-m) (1.14)

Использование формы с фиксированной точкой для представления смешанных (с целой и дробной частью) чисел в ЭВМ практически не встречается. Как правило, используются ЭВМ либо с дробной арифметикой (n = 0), либо с целочисленной арифметикой (m = 0).

Форма представления чисел с фиксированной точкой упрощает аппаратную реализацию ЭВМ, уменьшает время выполнения машинных операций, однако при решении задач на машине необходимо постоянно следить за тем, чтобы все исходные данные, промежуточные и окончательные результаты находились в допустимом диапазоне представления чисел. Если этого не соблюдать, то возможно переполнение разрядной сетки, и результат вычислений будет неверным. От этих недостатков в значительной степени свободны ЭВМ, использующие форму представления чисел с плавающей точкой, или нормальную форму.

В нормальной форме число представляется в виде произведения

X = m q^p ,

где: m – мантисса числа;

q – основание системы счисления;

p – порядок.

Для задания числа в нормальной форме требуется задать знаки мантиссы и порядка, их модули в q-ичном коде, а также основание системы счисления. Нормальная форма представления чисел неоднозначна, ибо взаимное изменение m и p приводит к перемещению точки (запятой). Отсюда произошло название формы представления чисел.

Например, десятичное число 73,28 в нормальной форме может быть записано в следующих вариантах:

X₍₁₀₎ = 73,28·10⁰ = 7,328·10¹ = 0,7328·10² = 0,07328·10³ = ... = 732,8·10^-1 и т. д.

Для однозначности представления чисел в ЭВМ используется нормальная нормализованная форма, в которой положение точки всегда задается перед значащей цифрой мантиссы, т. е. выполняется условие

q^-1 £ ïmï< q⁰ = 1 (1.15)

В общем случае разрядную сетку ЭВМ для размещения чисел в нормальной форме можно представить в виде, изображенном на рис. 1. б. Разрядная сетка содержит:

- разряд для знака мантиссы;

- r цифровых разрядов для q-ичного кода модуля мантиссы;

- разряд для кода знака порядка;

- s разрядов для q-ичного кода модуля порядка.

Диапазон представления модулей чисел в нормальной нормализованной форме определяется следующим неравенством:

_(1.16)

В конкретной ЭВМ диапазон представления чисел с плавающей точкой зависит от основания системы и числа разрядов для представления порядка.

Примерами применяемых форм чисел с плавающей точкой с различными основаниями системы счисления являются:

X = m·2 ^p , где 1/2£ïmï<1;

X = m·8 ^p , где 1/8£ïmï<1;

X = m·16 ^p , где 1/16£ïmï<1.

При этом у одинаковых по длине форматов чисел с плавающей запятой с увеличением основания системы счисления существенно расширяется диапазон представляемых чисел.

Точность вычислений при использовании формата с плавающей точкой определяется числом разрядов мантиссы r. Она увеличивается с увеличением числа разрядов.