Добавил:

kiss74 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет транспорта

Предмет:

Информатика

Файл:

Mathcad_для_экономистов_Голдобина_2

.pdf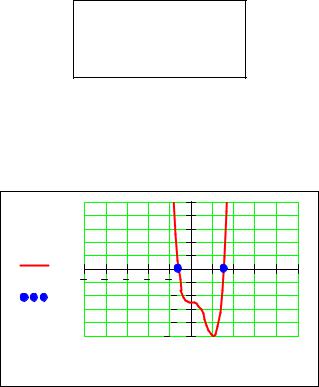

Скачиваний:

Добавлен:

05.07.2022

Размер:

885.22 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 119 10 11 > Следующая >>>

æ −5 ö

ç ÷

ç 0 ÷

v := ç −3 ÷

çç −14÷÷ è 12 ø

Применим функцию polyroots(v), возвращающую все корни полинома. Век- тор X содержит четыре корня полинома, из которых два − комплексные.

	æ	−0.66	ö
X := polyroots (v)	X = ç	0.179+ 0.631i÷
	ç		÷
	ç	0.179− 0.631i÷
	è	1.468	ø

Для графической интерпретации полученного решения задаем функцию по- линома g(x), создаем ряд значений аргумента x для корректного построения графика и вводим ранжированную переменную для нумерации элементов век- тора X:

g(x) := 12x4 − 14x3 − 3x2 − 5 x:= −5, −4.9.. 5

ORIGIN:= 1

j := 1.. 4

Далее вставляем графическую область, на которой в левый местозаполни- тель вводим через запятую функцию g(x) переменной x и функцию g(Xj) для каждого действительного корня Xj. Для изображения корней в виде точек на вкладке Traces (Линии графика) окна форматирования графика для второго графика (trace 2) изменяем тип линии (Type) − points (точки) и толщину линии

(Weight):

		10
		8
		6
	g(x)	4
	g(x)	2
	g(Xj)	2
	g(Xj)	5 4 3 2 12 0 1 2 3 4 5
		4
		6
		8
		10
		x, Xj
		81

5 Выполнить задание 3.

Задание 3. Решить систему линейных уравнений (таблица 4.3):

1)используя функцию find;

2)матричным способом;

3)используя функцию lsolve;

4)методом Гаусса (используя функцию rref).

Таблица 4.3 − Системы линейных уравнений

Вари-

Система

ант

линейных уравнений

ì1,4x1 + 2,1x2 - 3,3x3 +1,1x4

= 10;

-1,7x2 +1,1x3 -1,5x4

= 1,7;

ï10x1

ï2,2x1 + 34,4x2 -1,1x3 -1,2x4 = 2;

ï1,1x +1,3x

+1,2x

+1,4x

= 1,3

ì1,7x1 + 9,9x2

- 20x3 -1,7x4

= 1,7;

+ 0,5x2 - 30,1x3 -1,1x4

= 2,1;

ï20x1

- 20x2 + 30,2x3 + 0,5x4

= 1,1;

ï10x1

ï3,3x - 0,7x

+ 3,3x + 20x

= -1

ì3,3x1 - 2,2x2 -10x3 +1,7x4

= 1,1;

+ 21,1x2 +1,3x3-2,2x4

= 2;

ï1,8x1

- 4,5x4 = 1;

ï-10x1 +1,1x2 + 20x3

-1,7x2 - 2,2x3 + 3,3x4

= 2,1

î70x1

ì13,2x1 - 8,3x2 - 4,4x3 + 6,2x4 = 6,8;

+ 4,2x2

- 5,6x3

+ 7,7x4

=12,4;

ï8,3x1

- 3,7x2

+ 12,4x3 - 6,2x4

= 8,7;

ï5,8x1

ï3,5x

+ 6,6x

-1,8x

- 9,3x

= -10

ì4,2x1

+ 3,2x2 - 4,2x3

+ 8,5x4

= 13,2;

- 4,3x2

+12,7x3

- 5,8x4

= -4,1;

ï6,3x1

- 22,3x2 - 5,2x3

+ 4,7x4

= 6,4;

ï8,4x1

+13,7x2 + 6,4x3 -12,7x4

= 8

î2,7x1

ì4,8x1

+12,5x2 - 6,3x3 - 9,7x4

= 3,5;

- 31,7x2

+12,4x3 - 8,7x4

= 4,6;

ï22x1

+ 21,1x2 - 4,5x3

+14,4x4

= 15;

ï15x1

-14,4x2

+ 6,2x3 + 2,8x4

= -1,2

î8,6x1

Вари-

Система

ант

линейных уравнений

ì1,1x1 +11,3x2 -1,7x3 +1,8x4

= 10;

-11,7x2

+1,8x3

+1,4x4

= 1,3;

ï1,3x1

-1,7x3 -1,5x4

= 1,1;

ï1,1x1 -10,5x2

ï1,5x - 0,5x

+1,8x

-1,1x

= 10

ì1,7x1 -1,3x2 -1,1x3 -1,2x4

= 2,2;

-10x2 -1,3x3 +1,3x4

= 1,1;

ï10x1

+ 3,3x2

+1,2x3 +1,3x4

= 1,2;

ï3,5x1

+1,1x2 -1,3x3 -1,1x4

= 10

î1,3x1

ì8,1x1 +1,2x2 - 9,1x3 +1,7x4

= 10;

= 1,7;

ï1,1x1 -1,7x2 + 7,2x3 - 3,4x4

-1,8x2

+10x3 + 2,3x4

= 2,1;

ï1,7x1

ï1,3x +1,7x

- 9,9x + 3,5x

= 27,1

ì7,3x1+12,4x2 - 3,8x3 -14,3x4 = 5,8;

+12,5x3 + 6,6x4

= -6,6;

ï10,7x1 - 7,7x2

+14,4x3 - 8,7x4

= 12,4;

ï15,6x1 + 6,6x2

+12,2x2

- 8,3x3 + 3,7x4

= 9,2

î7,5x1

ì6,4x1

+ 7,2x2

- 8,3x3 + 42x4

= 2,23;

- 8,3x2 +14,3x3 - 6,2x4

= 17,1;

ï5,8x1

+ 7,7x2

-18,3x3

+ 8,8x4

= -5,4;

ï8,6x1

ï13,2x - 5,2x

- 6,5x +12,2x

= 6,5

ì7,3x1

- 8,1x2

+12,7x3

- 6,7x4

= 8,8;

- 8,3x3

+ 9,2x4

= 21,5;

ï11,5x1 + 6,2x2

- 5,4x2 + 4,3x3 - 2,5x4

= 6,2;

ï8,2x1

ï2,4x +11,5x

+ 3,3x

+14,2x

= -6,2

Окончание таблицы 4.3

Вариант	Система	Вариант	Система
	линейных уравнений		линейных уравнений

ì30,1x1 -1,4x2

+10x3

-1,5x4

= 10;

ì7,5x1 +1,8x2 - 2,1x3 - 7,7x4

= 1,1;

- 20x3

-1,4x4

= 1,5;

ï-17,5x1 +11,1x2 +1,3x3 - 7,5x4 = 1,3;

ï-10x1 +1,3x2

- 21,1x2

+ 7,1x3 -17,1x4 = 10;

+ 4,8x4

= 1,2;

ï1,7x1

ï2,8x1 -1,7x2 + 3,9x3

ï2,1x + 2,1x

+ 3,5x

+ 3,3x

= 1,7

-10x4

= -1,1

î10x1 + 31,4x2 - 2,1x3

ì1,1x1

+ 11,2x2

+11,1x3 -13,1x4 = 1,3;

ì35,1x1

+1,7x2 + 37,5x3 - 2,8x4 = 7,5;

+ 21,1x2

-1,1x3

-1,2x4

= 11,1;

ï- 3,3x1 +1,1x2 + 30,1x3 - 20,1x4 = 1,1;

ï45,2x1

+1,1x3

+10x4

= 20;

+18,1x2

- 31,7x3

+ 2,2x4 = 0,5;

ï7,5x1 + 1,3x2

ï31,7x1

+ 7,5x2

-1,8x3

+ 2,1x4

= 1,1

-1,5x4 = 2,1

î1,7x1

î- 21,1x1 + 31,7x2 +1,2x3

Пример выполнения задания 3

ì2,5x1 + 4,5x2 - 0,5x3 = 16,7;

Решить систему линейных уравнений

í-3,1x1 + 5,7x2 +11,4x3 = -5,8;

= -21,3.

î0,9x1 -8,3x2 + 42,3x3

1-й способ. Зададим произвольное начальное приближение всем неизвест- ным, входящим в систему:

x1 := 0 x2 := 0 x3 := 0

Напечатаем ключевое слово Given, ниже введем уравнения, составляющие систему, каждое в отдельном формульном блоке, используя логическое равен-

ство (Ctrl + =):

Given

2.5x1 + 4.5x2 - 0.5x3 16.7

-3.1x1 + 5.7x2 + 11.4x3		-5.8


0.9x1 - 8.3x2 + 42.3x3	-21.3

Определим вектор решений системы X и получим результат:

X := Find(x1, x2, x3)

æ 3.776 ö X = çç 1.583 ÷÷ è -0.273ø

2-й способ. Зададим матрицу коэффициентов при неизвестных системы и столбец свободных членов:

æ 2.5	4.5	-0.5ö	æ 16.7	ö
A := ç -3.1	5.7	11.4 ÷	b := ç -5.8	÷
ç		÷	ç	÷
è 0.9	-8.3	42.3 ø	è -21.3	ø

Вектор решений системы ищем в виде

X := A− 1 × b	æ 3.776		ö
X := A− 1 × b	X = ç	1.583	÷
	ç		÷
	è	-0.273ø

Для проверки правильности найденного решения системы, заданной в мат- ричном виде, достаточно вычислить произведение AX, которое должно быть равно вектору свободных членов:

æ 16.7 ö A × X = çç -5.8 ÷÷

è -21.3ø

Так как выполняется матричное равенство AX = b , то найдено верное реше- ние системы уравнений.

3-й способ. Зададим матрицу коэффициентов при неизвестных системы и столбец свободных членов. Вектор решений системы ищем в виде

æ 3.776		ö
X := lsolve(A ,b) X = ç	1.583	÷
ç		÷
è	-0.273ø

4-й способ. Зададим расширенную матрицу системы:

æ 2.5	4.5	-0.5	16.7	ö
AR := ç -3.1	5.7	11.4	-5.8	÷
ç				÷
è 0.9	-8.3	42.3	-21.3ø

Применим функцию rref(AR). Решением системы будет последний столбец полученной матрицы:

æ 1	0	0	3.776 ö	X := rref(AR)á3ñ	æ 3.776		ö
rref(AR) = ç 0	1	0	1.583 ÷	X := rref(AR)á3ñ	X = ç	1.583	÷
ç			÷		ç		÷
è 0	0	1	-0.273ø		è	-0.273ø

6 Выполнить задание 4.

Задание 4. Отделить решение системы нелинейных уравнений (таблица 4.4) графически, предварительно преобразовав уравнения к виду f 1(x) = y и f 2 (y)= x (f 2 (x)= y), и решить систему с помощью функции minerr. Сделать проверку.

Таблица 4.4 − Система нелинейных уравнений

	Вариант			Система нелинейных		Вариант		Система нелинейных
	Вариант				уравнений	Вариант			уравнений
					уравнений				уравнений

	1		ìcos y + 0,8x = 1,5;			9		ìsin(x +1) - y = 1,21;
	1		í			9		í
			î2y - sin(x - 0,6) = 1,2					î2,1x + 0,9 cos y =1,8
	2		ìsin(x + 0,2) + 2y = 2,3;			10		ìcos(x -1,2) + y = 0,4;
	2		í			10		í
			îcos( y - 0,8) + x = 0,7					îx - cos(0,9y) = 3,31
	3		ìcos(x + 0,3) + y = 1,5;			11		ìsin(x + 0,5) - y =1;
	3		í			11		í	- 2,3) + x = 0,3
			î2,2x -sin(y - 0,3) = 1,2					îcos( y	- 2,3) + x = 0,3
	4		ìsin(x -1,4) = 1,44 - y;			12		ìcos(x + 0,5) = 0,8 - y;
	4		í	- sin(y + 0,8) = 0,8		12		í	+ 0,2) =1,65 + 2,01x
			îx	- sin(y + 0,8) = 0,8				îsin(y	+ 0,2) =1,65 + 2,01x
	5		ìcos(0,6 + x) = 2,15 + y;			13		ìsin(x + 2) - 0,9y = 1,6;
	5		í			13		í	- 2) = 0,8 - x
			îsin y -1,8x -1,2 = 0					îcos( y	- 2) = 0,8 - x
	6		ìsin(y + 0,8) - x = 1;			14		ìcos( y -1) = 0,8 - 0,95x;
	6		í			14		í
			îcos(x + 0,04) = 2 -1,9y					î1,3y - sin(x + 0,1) = 3,5
	7		ìcos( y + 0,4) = 0,7 - x;			15		ìsin(2y -1) = 1,2 - x;
	7		í			15		í
			îsin(x - 0,4) = 1,6 + 2y					îsin(2x +1) = y - 0,7
	8		ìsin(y + 2,15) - x = 1,4;			16		ìcos(0,8y + 0,5) = 2 + 0,9x;
	8		í			16		í
			îcos(x - 2,1) = 0,55 - y					îsin x = 1+ 3y

					Пример выполнения задания 4
		Решить систему нелинейных уравнений						ìsin(3x - 2) - 2y = 2;
		Решить систему нелинейных уравнений						í
								î0,5x + cos(2y) = 1.
Вручную преобразовываем:

					y = sin(3x − 2) − 2	x =	1 − cos (2y)
					2			0.5		.
										.
В Mathcad задаем две функции:

f1(x) :=	sin(3x − 2) − 2	f2(y) :=	1 − cos (2y)
	2		0.5

и строим графики этих функций в одной координатной плоскости:

x := −5,−4.9.. 5			y := −2, −1.9.. 2
					2
					1.5
f1(x)					1
f1(x)					0.5
					0.5
y	5	4	3	2	01.5	0	1	2	3	4	5
					1
					1.5
					2
					x, f2(y)

По графику определяем начальное приближение одного из решений как точ- ку пересечения графиков, и применяем блок Given…minerr:

x := 1	y := −0.5
Given
sin(3x − 2) − 2y			2


0.5x + cos (2y)		1		1.056 ö


X := Minerr(x, y)		æ
X := Minerr(x, y)			X = ç	÷
		è		−0.54ø

Проверка показывает, что система решена верно:

ORIGIN:= 1

sin(3 X1 − 2) − 2 X2 = 2 0.5X1 + cos (2 X2) = 1

Остальные решения уточняются аналогично, изменяется только начальное приближение неизвестных x и y.

7 Выполнить задание 5.

Задание 5. Решить уравнение (таблица 4.5) в символьном виде с помощью:

1)функции root;

2)команд главного меню Symbolics / Variable / Solve (Символика / Пере- менная / Решение);

3)директивы solve палитры математических инструментов Symbolic (Сим- вольные или Ключевые слова);

4) блока Given…find.

Примеры и рекомендации по выполнению задания 5 см. в теоретической части лабораторной работы.

8 Выполнить задание 6.

Задание 6. Решить систему уравнений (таблица 4.5) в символьном виде:

1)воспользовавшись директивой solve палитры математических инструмен- тов Symbolic (Символьные или Ключевые слова);

2)с помощью блока Given…find.

Примеры и рекомендации по выполнению задания 6 см. в теоретической части лабораторной работы.

Таблица 4.5 − Примеры для символьного решения

Вариант

Уравнение

Система уравнений

ìxy = y

+1;

x +1

x -1

= 5

+ y 2 = 1

x + 3 x

îx

= 2x

ìx

+ y = 9a

;

x +1

2 y + y 2 = 6a3

îx

ì2x + y = a;

x(x +1)

îy - 2x = 2

x(x

-1)

ìxy + ay = 8;

(x 2 - x +1)2

îay + bx = 9

x +

= 4x 2 -1

ìx3

+ y = 2;

+ 3x

- 4y 2 + 4y = p

îy

3x -1

2x -1

x - 6

ìx2

+ y2

= p;

+ 4

x +1 x + 2

x -1

= 25

ï(x + y)

= 15

ìx = y - a 2 ;

(x + 2)2

+ y 2 = 9b

îx

æ x

ìx - y = 1- xy;

10ç

- a)x + y

= a

= 0

ì2x + 5y = a;

x +1

x + 2

x +

+ y

= b

îx

Окончание таблицы 4.5

Вариант

Уравнение

Система уравнений

3x - 5

+1 =

9x - x2 -8

ìx 2

+ y 2 = 2x;

x 2 -1

x -1

îy + ab = ax

x2 +

2 = 19

ìx + y = a;

(x -1)

îxy = b

- x - x

- x +1 = 2

ìx + y = a(1- xy);

îx + y + xy = 3

x2 - x + 3

x2 - x -1

+ 2 +

ìx

= 2ax + y;

= 5

îy 2 = x + 2ay

x2 + 2

æ x +1

ö2

æ x +1 ö

ìx + y = 2a;

= 14

+ y

= 2b

ø è x

îx

æ x - 3

ö2

æ x + 2 ö

ìx + y + a = 9;

+ ç

=10

= 81

x -1

è x

ø è

î2xy - b

ìx 2

+ xy = a;

x3 + 2

x3 + 3

+ y 2 = p

îxy

9 Распечатать лабораторную работу. Завершить работу с Mathcad.

Контрольные вопросы

1Назовите способы нахождения начального приближения корней уравнений.

2Какие функции для решения одного уравнения известны в Mathcad? В чем их от- личие?

3Какие аргументы функции root не обязательны?

4В каких случаях Mathcad не может найти корень уравнения?

5Как системная переменная TOL влияет на решение уравнения?

6Назовите функции для решения систем уравнений в Mathcad и особенности их применения. Дайте их сравнительную характеристику.

7Что такое вычислительный блок и какова его структура? Какой знак равенства ис- пользуется в блоке решения? Какой комбинацией клавиш вставляется в документ?

8Какие выражения недопустимы внутри блока решения уравнения?

9Какие уравнения называются матричными? Назовите способы решения матрич- ных уравнений.

10Перечислить способы символьного решения уравнений и систем уравнений в

Mathcad.

11Назовите особенности символьного решения уравнений, систем уравнений и не-

равенств.

ЛАБОРАТОРНАЯ РАБОТА № 5

АНАЛИТИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ В СИСТЕМЕ MATHCAD

Цель работы: получить начальные навыки работы с символьным процессо- ром системы Mathcad.

Способы выполнения символьных преобразований

Mathcad предоставляет следующие возможности для выполнения аналитиче- ских (символьных) преобразований:

∙в командном режиме − с помощью команд, содержащихся в главном меню

Symbolics;

∙символьные вычисления в реальном времени − основные символьные опе-

рации, выполняемые с помощью оператора символьного вывода →.

∙символьные операции, отсутствующие в меню Symbolics или в составе директив оператора символьного вывода →, но сводящиеся к ним в силу мате- матических соотношений и алгоритмов преобразований.

Инструментами аналитических преобразований в Mathcad служат:

∙меню Symbolics (Символика);

∙палитра Symbolic (Символьные или Ключевые слова) с панели мате- матических инструментов Math.

В качестве вспомогательных средств используются инструменты, пригодные для численных вычислений, например, находящиеся на палитрах Evaluation (Вычисление), Calculus (Высшая математика) и др.

Объекты символьных преобразований

Для успешного выполнения символьных операций необходимо четко пред- ставлять, над каким объектом будет совершено преобразование. Использование функций пользователя не допускается! Различают символьные операции:

∙с выделенной переменной;

∙с выделенным выражением.

В первом случае следует выделить синим управляющим курсором перемен- ную, во втором − выражение целиком. Если поместить курсор в произвольном месте формульного блока, то возможно получение логически неверного резуль- тата или появление диалогового окна, сообщающего об ошибке или отсутствии найденного символьного результата.

Выполняя символьные преобразования, необходимо помнить, что не всякое выражение поддается символьным расчётам. Если заданная операция невыпол- нима либо в силу того, что задача не имеет символьного решения, либо она яв- ляется слишком сложной для символьного процессора Mathcad, то система вы-

водит в дополнительном окне сообщение об ошибке либо просто возвращает исходное выражение.

Способы представления результатов вычисления

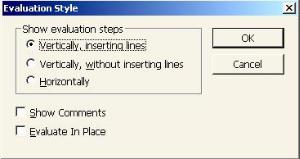
Установить размещение результатов символьных преобразований можно,

выбрав из главного меню Symbolics (Символика) команду Evaluation Style... − стиль представления результатов аналитических преобразований. Данная опе- рация выводит окно (рисунок 5.1), в котором выбирается:

∙Vertically, inserting lines (Вертикально, вставка строк) − расположение ре- зультата под основным выражением с включением пустых строк;

∙Vertically, without inserting lines (Вертикально, без вставки строк) − рас-

положение результата прямо под основным выражением;

∙Horizontally (Горизонтально) − расположение результата рядом, по гори- зонтали с основным выражением.

Кроме того, можно установить еще две опции:

∙Show Comments (Показать комментарии) − просмотр комментариев;

∙Evaluate In Place (Расчёт на месте) − заместить исходное выражение ре- зультатом его символьного преобразования.

Рисунок 5.1 − Стиль представления результатов аналитических преобразований

Обзор символьных операций меню Symbolics

Операции с выделенными выражениями

Для выполнения следующих операций выражение-операнд целиком выделя- ется синим управляющим курсором.

Evaluate (Вычислить) − преобразовать выражение с выбором вида преобра- зований из подменю. Подменю включает три операции:

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 119 10 11 > Следующая >>>

Соседние файлы в предмете Информатика

#
05.07.202262.09 Кб4Faylovy_menedzher (1).docx
#
05.07.2022885.22 Кб35Mathcad_для_экономистов_Голдобина_2.pdf
#
05.07.202246.99 Кб1Osnovy_formatirovania_dokumentov_v (1).docx
#
05.07.202222.5 Кб4Trebovania_otchet.docx
#
05.07.202248.45 Кб4Среда программирования IDLE.docx
#
08.07.20223.45 Mб19шпоры инфа 1 семестр.docx