
Mathcad_для_экономистов_Голдобина_2
.pdf∙ Symbolically [Shift+F9] (Символически) − обработка математических вы- ражений, содержащих встроенные в систему функции, выполнение всевозмож-
ных численных вычислений и представление выражения в наиболее простом виде.
∙Floating Point... (С плавающей точкой) – выполнить преобразование с ре- зультатом в форме числа с плавающей точкой (запятой). При выборе данной команды появляется окно, в котором можно задать количество цифр результата от 1 до 4000;
∙Complex (В комплексном виде) − выполнить преобразование с представ- лением результата в комплексном виде;
Simplify (Упростить) − упростить выделенное выражение с выполнением та- ких операций, как сокращение дробей, приведение подобных слагаемых, приве- дение к общему знаменателю, использование основных алгебраических и три- гонометрических тождеств;
Expand (Разложить по степеням, развернуть) − раскрыть скобки, предста- вить выражение в развернутом виде;
Factor (Разложить на множители) − разложить число или выражение на про- стые множители;
Collect (Разложить по подвыражениям) − собрать слагаемые, подобные вы- деленному выражению или переменной (приведение подобных слагаемых);
Polynomial Coefficients (Полиномиальные коэффициенты) − найти вектор коэффициентов полинома от заданной переменной. Перед выполнением опера- ции следует выделить переменную синим управляющим курсором.
Операции с выделенными переменными
К числу операций с выделенными переменными следует отнести содержа- щиеся в пункте подменю Variable (Переменная):
∙Solve − решить уравнение или неравенство относительно выделенной пе- ременной;
∙Substitute − заменить выделенную переменную содержимым буфера об- мена;
∙Differentiate − дифференцировать выражение по выделенной переменной (остальные переменные рассматриваются как константы);
∙Integrate − интегрировать выражение, содержащее выделенную перемен- ную, по этой переменной;
∙Expand to Series... (Разложить в ряд) − найти несколько (по умолчанию задано n = 6) членов разложения выражения в ряд Тейлора относительно выде-
ленной переменной;
∙ Convert to Partial Fraction (Разложить на элементарные дроби) − разло- жить на элементарные дроби выражение, которое рассматривается как рацио- нальная дробь относительно выделенной переменной.
91

Операции с выделенными матрицами
Операции с выделенными матрицами представлены в подменю Matrix (Мат- ричные операции):
∙Transpose (Транспонировать) − получить транспонированную матрицу;
∙Invert (Обратить) − создать обратную матрицу;
∙Determinant (Определитель) − вычислить детерминант (определитель) матрицы.
Операции данной группы выполняются над матрицами, а не над их иден- тификаторами!
Операции преобразования
В главном меню Symbolics (Символика) содержится раздел операций преоб- разования Transform со следующими возможностями:
∙Fourier Transform (Преобразование Фурье) − выполнить прямое преобра- зование Фурье относительно выделенной переменной;
∙Inverse Fourier Transform (Обратное преобразование Фурье) − выполнить обратное преобразование Фурье относительно выделенной переменной;
∙Laplace Transform (Преобразование Лапласа) − выполнить прямое преоб- разование Лапласа относительно выделенной переменной (результат − функция от переменной s);
∙Inverse Laplace Transform (Обратное преобразование Лапласа) − выпол-
нить обратное преобразование Лапласа относительно выделенной переменной (результат − функция от переменной t);
∙Z Transform (Z-преобразование) − выполнить прямое Z-преобразование относительно выделенной переменной (результат − функция от переменной z);
∙Inverse Z Transform (Обратное Z-преобразование) − выполнить обратное Z-преобразование относительно выделенной переменной (результат − функция от переменной n).
Обзор директив палитры Symbolic
Палитра математических инструментов Symbolic (Символические или Клю- чевые слова) (рисунок 5.2), в основном дублирует по смыслу команды главного меню Symbolic (Символика). Существенно отличается только способ примене- ния директив: ключевые слова отображаются на экране, а операнды вводятся в
соответствующие местозаполнители:
sin(x)2 + cos (x)2 simplify → 1 .
92
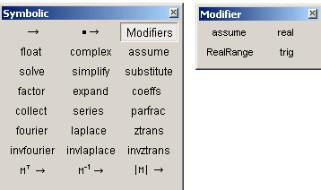
Рисунок 5.2 − Палитры директив символьных операций
Палитра Symbolic содержит директивы:
∙float – преобразование чисел в формат с плавающей точкой;
∙complex – преобразование в комплексной форме;
∙assume – присваивание переменным неопределенного значения, а также задание ограничений на значения или тип переменных;
∙solve − разрешить выражение относительно указанной переменной;
∙simplify – упрощение выражений;
∙substitute − выполнение замены;
∙factor – разложение выражения на простые дроби;
∙expand – разложение выражения по степеням;
∙coeffs – возвращение вектора с коэффициентами полинома;
∙collect − приведение подобных;
∙series – разложение в ряд по заданным переменным;
∙parfrac – разложение на элементарные дроби;
∙fourier – прямое преобразование Фурье;
∙laplace – прямое преобразование Лапласа;
∙ztrans – прямое Z-преобразование;
∙invfourier – обратное преобразование Фурье;
∙invlaplace – обратное преобразование Лапласа;
∙invztrans – обратное Z-преобразование;
∙MT → – транспонирование матрицы;
∙M-1 → – инвертирование матрицы;
∙|M| → – вычисление определителя матрицы;
∙Modifier – модифицированные команды:
–assume – вводное слово для приведенных ниже определений;
–real – значения переменной ограничиваются действительными числами;
–RealRange – значения действительной переменной ограничиваются интер- валом [a, b];
–trig – направление тригонометрических преобразований.
93

Вычисление производных, интегралов, сумм, произведений и пределов
Ряд возможностей для проведения символьных преобразований предостав- ляют операторы палитры Calculus (Исчисление) – операторы знаков математи- ческого анализа, некоторые из которых дают возможность выполнения числен- ных расчетов (рисунок 5.3).
Рисунок 5.3 − Палитра операторов высшей математики
Технология работы с операторами палитры Calculus проста:
∙вставляется шаблон требуемого оператора с палитры или комбинацией клавиш быстрого доступа (таблица 5.1);
∙шаблон заполняется согласно общепринятым математическим правилам;
∙выражение вычисляется в символьном (оператор «→») или численном (оператор «=») виде.
Таблица 5.1 − Операторы палитры Calculus
Команда |
Комбинация клавиш |
Описание шаблона оператора |
|
Shift + / |
Производная первого порядка |
|
|
|
|
Ctrl + Shift + / |
Производная порядка n |
|
|
|
|
Ctrl + Shift + Z |
Бесконечность |
|
|
|
|
Shift + 7 |
Определенный интеграл |
|
|
|
|
Ctrl + I |
Неопределенный интеграл |
|
|
|
|
Ctrl + Shift + 4 |
Сумма ряда |
|
|
|
|
Shift + 4 |
Суммирование по ранжированной переменной |
|
|
|
|
Ctrl + Shift + 3 |
Итерационное произведение |
|
|
|
|
Shift + 3 |
Произведение по ранжированной переменной |
|
|
|
94

Окончание таблицы 5.1
Команда |
Комбинация клавиш |
Описание шаблона оператора |
|
Ctrl + L |
Предел |
|
|
|
|
Ctrl + Shift + A |
Правосторонний предел (предел справа) |
|
|
|
|
Ctrl + Shift + B |
Левосторонний предел (предел слева) |
|
|
|
Производные, суммы, произведения и интегралы находят широкое примене- ние при решении экономических задач.
Пример 5.1. Годовая процентная ставка начисления сложных процентов за кредит установлена на уровне 6 % плюс надбавка величиной 0,6 % от суммы ссуды в первые два года и 0,8 % − в следующие два года. Определите величину множителя наращения к концу срока кредита.
Решение.
Величина множителя наращения при использовании схемы сложных про-
центов с переменной процентной ставкой вычисляется по формуле
n |
+ ik )tk −tk −1 . |
∏(1 |
|
k=1 |
|
Процентную ставку начисления сложных процентов и периоды времени представим в виде векторов:
æ 6 |
ö |
æ 0 |
ö |
|
i := ç |
0.6 |
÷ |
t := ç 2 |
÷ |
ç |
|
÷ |
ç |
÷ |
è |
0.8 |
ø |
è 4 |
ø |
2 |
(1 + 0.01i0 + 0.01 ik)t k−t k−1 = 1.296 |
|||
∏ |
||||
k = 1
Пример 5.2. Определить суммарный выпуск продукции (Q), суммарные за- траты (C) и суммарную прибыль (PR) за несколько лет (T) по функции выпуска tn, зависящей от времени.
Решение.
Определим суммарный выпуск продукции:
|
|
óT |
|
|
-t |
(n+ 1) |
|
T |
|
|
Q |
|
ô tn dt ® Q |
|
lim |
|
+ Tn |
|
|
||
|
|
|
|
|
||||||
|
õ0 |
|
t → 0 |
(n + 1) |
|
(n + 1) |
. |
|||
Затраты линейно зависят от выпуска продукции. Суммарные затраты за не- сколько лет:
95

C |
|
ôóT (a + b tn)dt ®C |
|
lim |
-a t - |
t(n+1) |
|
b + T |
(a n + a + Tn b) |
|
|
|
|
|
|
|
|||||||
|
(n + 1) |
(n + 1) |
|
|
|||||||
|
õ |
|
t → 0 |
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
. |
||
Пусть функция спроса равна P. Тогда суммарная прибыль при исходных
функциях выпуска и затрат
|
|
õ0 |
|
t → 0 |
(n + 1) |
(n + 1) |
|
|
|
óT |
|
|
(n+1) |
(n+1) |
( n |
n ) |
. |
||
Задание операторов пользователя
В Mathcad существует возможность задавать не только функции, но и опе-
раторы пользователя.
Для ввода символа нового оператора можно обратиться в центр ресурсов
Mathcad из главного меню Help / Resource Center / QuickSheets and Reference Table / Extra Math Symbols (Помощь / Центр Ресурсов / Краткое руководство и справочный стол / Дополнительные математические символы), выбрать и ско- пировать в буфер обмена символ. Оператор пользователя задается как обыкно- венная функция:
x ∙ y x2 + y2 .
Далее его можно использовать как функцию и как оператор:
x:= 2 |
y := 3 |
|
∙(x, y) = 13 |
|
|
x ∙ y = 13 |
|
. |
Применять новый оператор можно с помощью шаблона палитры математи- ческих знаков Evaluation, например, используя кнопку 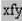 (Инфиксный опера-
(Инфиксный опера-
тор). В результате нажатия появляется шаблон 

 , в средний местозаполни- тель которого вводится символ оператора, а по краям − операнды. Можно зада- вать операторы для работы с одним или несколькими операндами. Например,
, в средний местозаполни- тель которого вводится символ оператора, а по краям − операнды. Можно зада- вать операторы для работы с одним или несколькими операндами. Например,
элементарный шаблон пересчета валют создается и используется следующим образом:
Euro(x) := x × 1.367 |
S := 1 |
|
Euro = |
S |
|
5Euro = |
6.835S |
|
|
|
|
96
Порядок выполнения лабораторной работы
1Загрузить Mathcad. Сохранить документ с именем ФИОСтудента5.
2Ввести в поле документа данные о студенте и выполняемой работе.
3Установить удобный способ представления результатов символьных пре- образований и отображение комментариев, выбрав из главного меню Symbolics (Символика) команду Evaluation Style...
4Выполнить задание 1.
Задание 1. Используя команду Symbolics / Evaluate / Floating Point... (Сим-
волика / Вычислить / С плавающей точкой…), представить числа в указанном виде (таблица 5.2).
Таблица 5.2 − Символьные вычисления с плавающей точкой
Вариант |
Задание |
Вариант |
Задание |
|
|
|
|
|
|
1 |
Число π в 5 позициях; |
9 |
Число π в 9 позициях; |
|
число 32,345667 в 4 позициях |
число 94,678277 в 5 позициях |
|||
|
|
|||
|
|
|
|
|
2 |
Число e в 8 позициях; |
10 |
Число e в 7 позициях; |
|
число 14,83254 в 3 позициях |
число 26,357826 в 4 позициях |
|||
|
|
|||
|
|
|
|
|
3 |
Число π в 4 позициях; |
11 |
Число π в 7 позициях; |
|
число 76,867333 в 3 позициях |
число 38,9356324 в 6 позициях |
|||
|
|
|||
|
|
|
|
|
4 |
Число e в 7 позициях; |
12 |
Число e в 11 позициях; |
|
число 67,09801347 в 5 позициях |
число 55,7737575 в 3 позициях |
|||
|
|
|||
|
|
|
|
|
5 |
Число π в 6 позициях; |
13 |
Число π в 11 позициях; |
|
число 26,92745433 в 5 позициях |
число 35,1557545 в 4 позициях |
|||
|
|
|||
|
|
|
|
|
6 |
Число e в 9 позициях; |
14 |
Число e в 12 позициях; |
|
число 53,3455567 в 4 позициях |
число 15,451145 в 5 позициях |
|||
|
|
|||
|
|
|
|
|
7 |
Число π в 10 позициях; |
15 |
Число π в 12 позициях; |
|
число 41,3245467 в 6 позициях |
число 918,321645 в 5 позициях |
|||
|
|
|||
|
|
|
|
|
8 |
Число e в 10 позициях; |
16 |
Число e в 9 позициях; |
|
число 75,87674343 в 7 позициях |
число 7,4561871 в 5 позициях |
|||
|
|
|||
|
|
|
|
5 Выполнить задание 2.
Задание 2. Используя команду Symbolics / Evaluate / Complex (Символи-
ка / Вычислить / В комплексном виде), представить числа в комплексной форме (таблица 5.3). Для второго и третьего выражения выполнить
Symbolics / Evaluate / Symbolically (Символика / Вычислить / Символически).
97
Таблица 5.3 − Символьные вычисления в комплексном виде |
|
|
|
|
|
|
|||||||||||
Вариант |
|
|
Задание |
|
|
|
Вариант |
|
|
Задание |
|
|
|
|
|
|
|
|
|
|
|
|
e1+ |
π |
|
|
|
ctg(b −23 ) ; e3+ |
π |
|
|
|
|||
1 |
4 |
− 7 ; |
ctg(a −3 ) ; |
4 i |
9 |
4 |
− 61 ; |
5 i |
|
|
|
||||||
|
|
|
|
|
|
π |
|
|
|
|
|
e1+ |
π |
|
|||
2 |
|
− 8 ; |
tg(a −3 ) ; e3+ 4 i |
10 |
4 |
− 31 ; |
ctg((a − 2) −3 ) ; |
6 i |
|||||||||
3 |
|
−11 ; |
tg(a −2 ) ; |
e |
3+ |
π i |
11 |
|
− 71 ; |
tg((b + 3) −3 ) ; |
e |
1,5+ |
π i |
||||
|
4 |
|
12 |
|
|
|
|
3 |
|||||||||
|
|
|
|
|
|
|
π |
|
|
|
ctg(a −11 ) ; e2+ |
π |
|
|
|||
4 |
6 |
−17 ; |
ctg(a −5 ) ; |
e1+ 6 i |
12 |
4 |
−13 ; |
6 i |
|
|
|||||||
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
e3+ |
π |
||
5 |
|
− 26 ; |
tg(b −3 ) ; |
e2+ 3 i |
13 |
6 |
−86 ; |
tg((a + 2) −43 ) ; |
6 i |
||||||||
6 |
|
− 27 ; |
ctg(a −63 ) ; |
e |
1+ π i |
14 |
|
− 54 ; tg(b − a −3 ) ; e |
1+ |
π i |
|
|
|||||
|
4 |
2 |
|
|
|
|
15 |
|
|
||||||||
|
|
|
|
|
|
|
π |
|
|
|
|
|
e1+ |
π |
|
||
7 |
4 |
− 47 ; |
tg(x −1 ) ; |
e3+ 48 i |
15 |
6 |
− 71 ; |
tg((a +1) −3 ) ; |
3 i |
||||||||
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
π |
|
|
8 |
6 |
− 53 ; tg(b −33 ) ; |
e2+12 i |
16 |
6 |
−117 ; tg(9a −5 ) ; e1+ 24 i |
|
||||||||||
6 |
Выполнить задание 3. |
|
|
|
|
|
|
|
|
|
|
|
|||||
Задание 3. Для полинома g(x) (таблица 5.4) выполнить следующие действия: |
|||||||||||||||||
1)разложить на множители, используя команду Symbolics / Factor (Симво- лика / Разложить на множители);
2)заменить переменную x на выражение y + z в g(x), используя операцию
Symbolics / Variable / Substitute (Символика / Переменная / Заменить);
3)полученное в 2) выражение разложить по степеням (раскрыть скобки), используя операцию Symbolics / Expand (Символика / Развернуть);
4)используя команду Symbolics / Collect (Символика / Собрать), свернуть выражение, полученное в 3), по переменной z (привести подобные слагаемые);
5)решить полиномиальное уравнение g(x) = 0. Для этого необходимо за- дать полином g(x), установить курсор на переменную x и использовать команду Symbolics / Variable / Solve (Символика / Переменная / Решить).
98

Таблица 5.4 − Полином
Вариант |
|
|
|
g(x) |
Вариант |
|
|
|
|
g(x) |
|
|
1 |
x4 − 6x 2 |
+12x − 8 |
9 |
x4 |
+ 5x3 |
+ 9x 2 + 5x − 2 |
|
|||||
2 |
x4 + 6x3 |
+11x2 − 2x − 28 |
10 |
x4 |
+ 6x3 |
+13x2 +10x + 2 |
|
|||||
3 |
x4 + 4x3 − 4x2 + 4x − 5 |
11 |
x4 + 2x3 |
+ x 2 |
+ 2x − 6 |
|
||||||
4 |
x4 |
−10x3 +16x + 5 |
12 |
x4 |
− x3 − 7x 2 |
− 8x − 6 |
|
|||||
5 |
x4 + x3 |
− 4x2 +16x − 8 |
13 |
x4 |
+ 3x3 |
|
+ 4x 2 + x − 3 |
|
||||
6 |
x4 |
+ x3 |
+ 2x − 4 |
14 |
2x 4 − 7x3 − 23x 2 + 43x −15 |
|
||||||
7 |
x4 |
− 6x3 |
+11x 2 + 2x − 28 |
15 |
x4 |
− 3x3 |
|
− 3x2 +11x − 6 |
|
|||
8 |
x4 |
− 3x3 |
+ 3x 2 − 2 |
16 |
x4 |
− 2x3 |
−13x 2 + 38x − 24 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример выполнения задания 3 x4 − 2x3 − 6x2 + 7x + 6
1) Зададим полином, выделим его синим управляющим курсором целиком и выберем из главного меню последовательно Symbolics / Factor (Символи- ка / Разложить на множители):
4 |
3 |
2 |
+ 7 x + 6 |
(x + 2) (x − 3) |
( 2 |
) |
|
x |
− 2 x |
− 6 x |
x |
− x − 1 |
. |
2) Напечатаем выражение замены y + z, выделим его синим управляющим курсором целиком и скопируем в буфер обмена комбинацией клавиш Ctrl + C. В полиноме g(x) установим управляющий курсор на переменную x и выполним последовательность команд Symbolics / Variable / Substitute (Символи- ка / Переменная / Заменить). В результате получим:
(y + z)4 − 2 (y + z)3 − 6 (y + z)2 + 7 y + 7 z + 6 .
3) Выделим полученное в 2) выражение синим управляющим курсором це- ликом и выполним Symbolics / Expand (Символика / Развернуть):
.
4) Установим управляющий курсор на переменную z и выполним приведе- ние подобных Symbolics / Collect (Символика / Собрать):
z4 + (−2 + 4y)z3 + (−6y − 6 + 6y2)z2 + (−6y2 − 12y + 4y3 + 7)z + y4 + 6 + 7y − 2y3 − 6y2 .
5) В полиноме g(x) установим управляющий курсор на переменную x и вы- полним последовательность команд Symbolics / Variable / Solve (Символи- ка / Переменная / Решить). Полученный результат упростим:
99

|
|
x4 − 2x3 − 6x2 + 7x + 6 |
æ |
|
|
|
−2 |
|
|
ö |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
3 |
|
|
|
÷ |
|
|
æ |
−2 |
|
ö |
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
|
÷ |
|
|
ç |
3 |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
ç |
1 |
|
|
5 |
+ |
1 ÷ |
= |
ç |
|
÷ |
|
|||||
|
|
|
|
|
|
|
|
|
|
ç |
2 |
|
|
2 |
÷ |
ç |
|
|
÷ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
÷ |
|
|
ç 1.618 |
|
÷ |
|
||||
|
|
|
|
|
|
|
|
|
|
ç |
1 |
|
− |
1 |
5 ÷ |
|
|
è −0.618ø |
|
|||||||
|
|
|
|
|
|
|
|
|
|
è 2 |
|
|
|
2 |
|
|
ø |
|
|
|
|
|
|
|
||
7 Выполнить задание 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Задание 4. Определить символьное значение первой и второй производных |
||||||||||||||||||||||||||
функции f(x) (таблица 5.5), установив курсор на переменную x и используя ко- |
||||||||||||||||||||||||||
манду Symbolics / Variable / Differentiate (Символика / Переменная / Диффе- |
||||||||||||||||||||||||||
ренцировать). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5.5 − Функции для дифференцирования |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Вариант |
|
|
|
|
f(x) |
|
|
Вариант |
|
|
|
|
|
|
|
|
|
|
|
|
f(x) |
|
|
|
||
1 |
arccos 2 - x |
|
|
|
|
9 |
ln |
e x |
+ 2 + |
|
e2x |
+ 4e x |
+1 |
|||||||||||||
|
|
x 2 |
|
|
|
|
ex |
+ 2 - e2x + 4e x +1 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2 |
arctg x +1 |
|
|
|
|
10 |
|
2 |
|
arctg 2x +1 |
|
|
|
|
||||||||||||
|
|
x -1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||
3 |
ln |
a + be x |
- |
a |
|
|
11 |
ln a + b cos nx + |
b2 |
- a 2 sin nx |
||||||||||||||||
|
|
a + be x |
+ |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
a + b cos nx |
||||||||
4 |
arcsin |
1− x2 |
|
|
|
12 |
|
x |
2 |
- a |
2 |
+ a arcsin |
|
a |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||||||||
5 |
arccos(3x - 4x3 ) |
|
|
13 |
|
x ln( |
|
x + |
|
x + a) - |
x + a |
|||||||||||||||
6 |
arcsin |
1 |
2x |
|
|
|
|
14 |
ln tg |
x |
- ctg x ln(1+ sin x) - x |
|||||||||||||||
|
|
|
+ x2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
7 |
1 |
arctg |
x |
3 |
|
|
|
15 |
ln x2 |
+ x |
|
2 +1 + |
1 |
arctg x 2 |
||||||||||||
|
3 |
|
|
1- x2 |
|
|
|
|
|
|
x 2 - x 2 +1 2 2 |
1- x 2 |
||||||||||||||
|
x 2 |
ln x |
- |
1 |
ln |
a |
+ bx |
2 |
|
|
1 |
|
|
|
|
|
|
æ |
|
b |
|
ö |
|
|||
8 |
|
|
2 |
|
|
16 |
|
|
|
|
|
|
|
ç |
|
tg x |
÷ |
|
||||||||
a + bx |
|
b |
|
|
|
|
|
|
|
|
|
arctg |
|
|
÷ |
|
||||||||||
|
|
|
|
|
|
|
|
|
ab |
|
|
|
|
ç |
|
a |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
ø |
|
||||||
8 Выполнить задание 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Задание 5. Получить первообразную функции f(x) (таблица 5.6), для чего ус- |
||||||||||||||||||||||||||
тановить курсор на переменную x и использовать команду Symbolics / Variable |
||||||||||||||||||||||||||
/ Integrate (Символика / Переменная / Интегрировать). |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
