Mathcad_для_экономистов_Голдобина_2

График функции в декартовой системе координат

Для построения графиков функций одной переменной в декартовой системе координат в Mathcad предусмотрены способы: упрощенный («быстрый»), с ис- пользованием ранжированной переменной, по массивам данных.

Для построения двумерного графика достаточно вызвать шаблон X-Y Plot

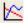, в знакоместо по оси абсцисс вписать имя переменной, а в знакоместо по оси ординат вписать функцию и щелкнуть левой клавишей мыши. При этом многие параметры задаются автоматически, например, пределы изменения ар- гумента устанавливаются от минус 10 до 10 или от 0 до 10.

Примечание − Для построения в одной координатной плоскости графиков двух и более функций их имена или определяющие выражения перечисляются в знакоместе по оси ординат через запятую.

Система Mathcad дает возможность построения графиков по данным, пред- ставленным векторами, матрицами или таблицами данных, что бывает необхо- димо при решении ряда прикладных задач. Для этого достаточно задать масси- вы и вписать их имена в соответствующие знакоместа шаблона:

Большие возможности предоставляет поэтапное построение графиков с ис- пользованием ранжированной переменной:

1)определяется функция пользователя;

2)задается ранжированная переменная на некотором диапазоне с требуе- мым шагом;

3)вставляется шаблон графика;

4)в соответствующие знакоместа вводятся имена аргумента и функции.

Например, построение графика функции f (x) = x3 − x − 2 будет выглядеть следующим образом:

31

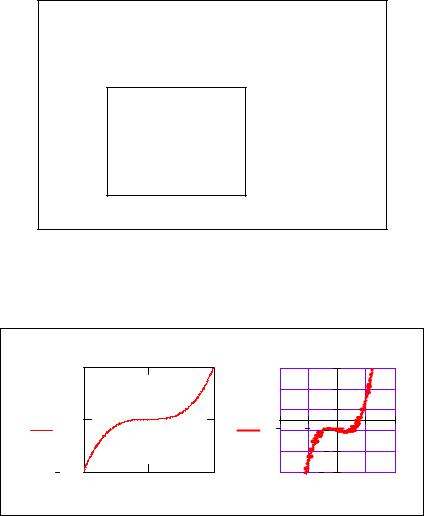
f(x) := x3 − x − 2 - функция пользователя

x:= −2, −1.8.. 2 - ранжированная переменная, заданная на симметричном диапазоне с шагом 0,2

f(x)

x

Каждый из описанных способов имеет свои преимущества и недостатки. Так, построенные упрощенным способом графики ввиду автоматически вы-

бранных границ отображения могут не отражать существенные особенности функции. Устранить возникший недочет можно, уменьшив пределы изменения аргумента или функции (рисунок 2.5).

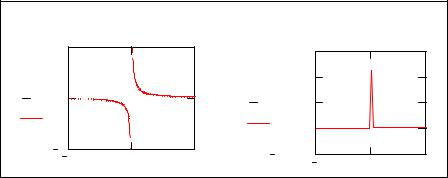
Использование ранжированной переменной позволяет варьировать шаг ме- жду узловыми точками графика от значительного (для построения диаграмм и точечных зависимостей) до мелкого (для более точного отображения непрерыв- ных зависимостей). Но при данном способе возможно появление ошибок при построении функций с особенностями или ограниченной областью определе- ния. На рисунке 2.6 слева представлен график, построенный «быстрым» спосо- бом, а справа – ошибочный, с помощью ранжированной переменной.

32

Рисунок 2.6 − Способы построения графика функции y = 1/x

Форматирование двумерных графиков

Для изменения формата уже построенного графика необходимо сначала ак- тивизировать соответствующую графическую область, щелкнув левой клави- шей мыши в поле графика. Перемещение, копирование, изменение размеров графической области выполняется согласно общим для областей Mathcad пра- вилам.

Окно форматирования текущего графика функции в декартовой системе ко-

ординат (Formatting Currently Selected X-Y Plot) можно вызвать одним из сле-

дующих способов:

∙последовательностью команд главного меню Format / Graph / X-Y Plot… (Формат Декартовых графиков...);

∙двойным щелчком левой клавишей мыши в области графика;

∙щелчком правой клавишей мыши в графической области с последующим выбором из контекстного меню команды Format…

Диалоговое окно форматирования имеет четыре вкладки:

∙X-Y Axes (X-Y Оси) – изменение параметров осей;

∙Traces (Тип линий) – изменение линий графика;

∙Labels (Метки) – управление надписями на графике;

∙Defaults (По умолчанию) – задание опций по умолчанию.

На вкладке X-Y Axes (рисунок 2.7) содержатся следующие опции, относя- щиеся к оси абсцисс и оси ординат, соответственно поля Х-Axis и Y-Axis:

∙Log Scale (Логарифмическая шкала) – установка логарифмического мас- штаба, полезного в случае различия данных на несколько порядков;

∙Grid Lines (Сетка) – установка вспомогательных линий сетки;

∙Numbered (Нумерация) – установка числовых данных по осям. Если фла- жок снят, то числовые данные не отображаются;

33

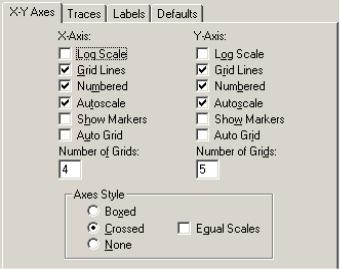
∙Autoscale (Автоматическая шкала) – автоматическое масштабирование, выбор диапазона осей производится процессором Mathcad;

∙Show Markers (Показать отметки) – установка вспомогательных линий- маркеров. При выборе этой опции вдоль соответствующей оси появляются два знакоместа, позволяющие вводить числовые данные. Эти данные отобразятся в виде подписи на пунктирной линии-маркере, пересекающей графическую об- ласть перпендикулярно выбранной оси;

∙Auto Grid (Автосетка) – автоматическая установка вспомогательных линий сетки производится процессором Mathcad. Для установки желаемого количества линий флажки необходимо снять;

∙Number of Grids (Число линий) – установка необходимого числа вспомога- тельных линий сетки.

Рисунок 2.7 − Вкладка форматирования осей графика

В поле Axes Style (Стиль осей координат) расположены следующие пере- ключатели, регулирующие отображение координатных осей:

∙Boxed (В рамке) – прямоугольное обрамление графика линиями, выпол- няющими функцию осей координат;

∙Crossed (Только оси) – отображение осей в виде прямых, пересекающихся

вначале координат;

∙None (Нет) – отсутствие осей.

Флажком Equal Scales (Равны), устанавливаются равные масштабы по осям.

34

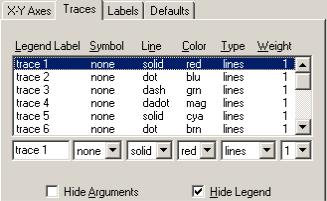
Следующая второй вкладка Traces (Тип линий) служит для управления ото- бражением линий графика. С помощью опций этой вкладки можно регулиро- вать следующие параметры (рисунок 2.8):

∙Legend Label (Надпись легенды, Метка) – текст, описывающий ряд дан- ных, имя линии графика;

∙Symbol (Символ) – выбор символа, которым отображаются узловые точки данных (для которых вычисляются координаты) на графике;

∙Line (Линия) – установка стиля линий (сплошная, пунктирная и т. п.);

∙Color (Цвет) – цвет линий и узловых точек данных;

∙Type (Тип) – тип представления графиков;

∙Weight (Толщина) – толщина линии и точек данных.

Приступая к форматированию линии графика, выберите щелчком мыши не- обходимую строку из представленного в окне форматирования списка, данные в

котором расположены в соответствии с порядком следования функций по оси ординат.

Рисунок 2.8 Вкладка форматирования линий графика

Раскрывающийся список Symbol (Символ) предлагает следующие маркеры для узловых точек графика выбранной функции:

∙none – без маркера;

∙×’s – крестик;

∙+’s – плюс;

∙box – квадрат;

∙dmnd – ромб;

∙o’s – окружность.

Раскрывающийся список Line (Линия) позволяет выбрать один из следую- щих стилей отображения линий:

∙solid – сплошная;

∙dot – пунктир;

35

∙dash – штрих;

∙dadot – штрих-пунктир.

Раскрывающийся список Color (Цвет) содержит основные цвета линий и уз- ловых точек.

Для установки типа графика имеются следующие возможности, перечислен- ные в раскрывающемся списке Type (Тип):

∙lines (линия) – построение линиями;

∙points (точки) – построение точками;

∙error (ошибки) – построение вертикальными черточками с оценкой интер- вала погрешностей;

∙bar (столбцы) – построение в виде гистограммы;

∙step (шаг) – построение ступенчатой линией;

∙draw (рисовать) – проводятся линии от точки до точки;

∙stem (стержень) – построение вертикальными линиями от оси абсцисс до узловых точек;

∙solid bar (сплошные столбцы) – построение в виде гистограммы с закра- шенными столбцами.

Еще два параметра вкладки Traces связаны с возможностью отображения на графике вспомогательных надписей:

∙Hide Arguments (Скрыть аргументы) – при установленном флажке матема- тические выражения по осям графика не отображаются;

∙Hide legend (Скрыть легенду) – при установленном флажке имена линий графиков не отображаются.

Третья вкладка окна форматирования Label (Метки) служит для установки отображения дополнительных надписей:

∙Title (Заголовок) – название графика;

∙X-Axis (Х-ось) – надпись по оси абсцисс;

∙Y-Axis (Y-ось) – надпись по оси ординат;

В поле Title вкладки Label (Метки) содержатся переключатели Above (Сверху) и Below (Снизу) и флажок Show Title (Показать заголовок), управ- ляющие отображением титульной надписи.

Вкладка Defaults (По умолчанию) служит для задания параметров графики по умолчанию:

∙Change to Defaults – вернуть значения по умолчанию;

∙Use for Defaults – использовать далее в документе параметры текущего графика в качестве значений по умолчанию.

Обычно форматирование графика предусматривает множественные преоб- разования. Поэтому для просмотра влияния отдельных установок или для на- значения большинства параметров без закрытия диалогового окна следует на- жимать кнопку Apply (Применить).

36

Порядок выполнения лабораторной работы

1Загрузить Mathcad. Сохранить новый документ с именем ФИОСтудента2. Периодически сохранять документ в процессе работы.

2Ввести в поле документа данные о студенте и выполняемой работе: Выполнил:

Студент группы Ф.И.О.

Вариант

Лабораторная работа № 2 Тема: Ранжированные переменные. Функции. Графики. Цель:

3 Выполнить задание 1.

Задание 1. В соответствии с вариантом таблицы 2.1 определить ранжиро- ванные переменные и показать их значения в таблицах вывода. Изменить поло- жение таблиц вывода относительно имен переменных. Показать одну таблицу вывода в матричном виде. Для других таблиц вывода установить отображение нумерации строк и столбцов.

Таблица 2.1 − Варианты заданий 1 и 2

37

Окончание таблицы 2.1