Добавил:

kiss74 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет транспорта

Предмет:

Информатика

Файл:

Mathcad_для_экономистов_Голдобина_2

.pdf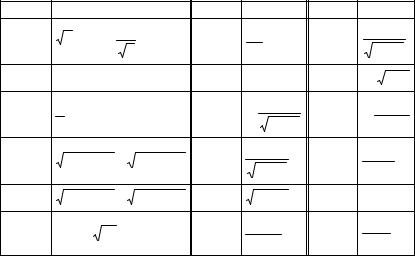

Скачиваний:

Добавлен:

05.07.2022

Размер:

885.22 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1111

Таблица 5.6 − Функции для интегрирования

Вариант

f(x)

Вариант

f(x)

Вариант

f(x)

x + ln x − 1

ln x − x

1− x 2

x ln x − x

ln sin x

x +1

x + ln cos x

3− x 2

2 tg

1− x 4

2 − x2

x2 + x +1 + x2 − x +1

x +1

−1

1− x 2

e x

+ 1

x 2

+ x +1 −

x 2 − x +1

1+ e−x

e2x sin 3x

(x +1)3 3 x2

cos 2x

tg 3x

cos x

tg x

9 Выполнить задание 6.

Задание 6. Разложите выражение (таблица 5.7) в ряд Тейлора заданного по-

рядка аппроксимации,

1)используя команду Symbolics / Variable / Expand to Series... (Символи-

ка / Переменная / Разложить в ряд);

2)в окрестности точки xо, используя директиву series (разложить в ряд) па- литры инструментов Symbolic (Символические или Ключевые слова).

Таблица 5.7 − Функции для разложения в ряд

Вариант	f(x)	x0	n	Вариант	f(x)	x0	n

1	x3 − 2ex −1	1	7	10	2 tg x	0	12
2	sin x − (x − 2) ln(x −1)	2	8	11	e x−3 − ln(x − 2)	3	8
3	cos x + ch x	0	5	12	log32 (x −1) + x2	2	6

4	x2 − 4x − (x −1) ln x	1	6	13	sh(x + 2)	-2	5

5	cos 2 (x − 3) + x2 − 3x	3	9	14	(x + 1) lg(x + 2)	-1	8

6	sin x − sh x	0	8	15	ecos x	0	5
7	sin 2 (x −1) + x	1	7	16	ctg x	π/2	12

8	(x −1)2 lg(x)	1	8	17	22 sin( x−1)	1	4
9	e2x +4 − x 2	-2	5	18	log3 (x − 4)	5	7

101

Пример выполнения задания 6

22tg ( x−2) , xо = 2, n = 3.

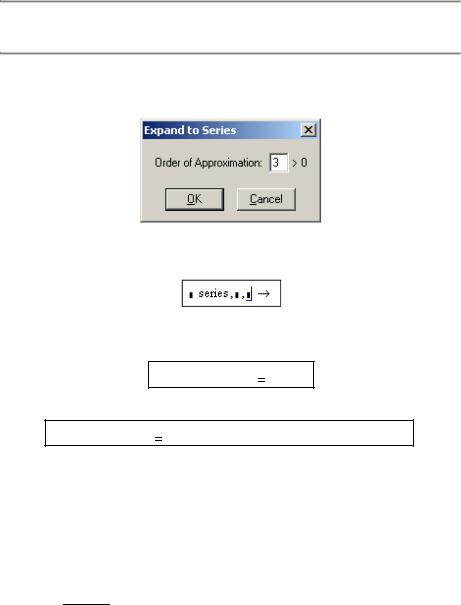
1) Введем функцию, установим курсор на переменную и выберем из глав-

ного меню последовательно Symbolics / Variable / Expand to Series... (Симво-

лика / Переменная / Разложить в ряд). В появившемся окне укажем порядок разложения n = 3:

После нажатия кнопки OK получим требуемое разложение.

2) Введем директиву series с палитры инструментов Symbolic (Символиче- ские или Ключевые слова):

В левый местозаполнитель введем функцию, а справа − точку, в окрестности которой происходит разложение в ряд, с использованием логического знака ра- венства. Далее, через запятую, введем порядок аппроксимации:

22 tan(x−2) series , x 2, 3 →

В результате получим

22 tan(x−2) series , x 2, 3 → 1 + 2ln(2)(x − 2) + 2ln(2)2 (x − 2)2 .

10Выполнить задание 7.

Задание 7. Разложите выражения (таблица 5.8) на элементарные дроби, ис-

пользуя последовательность команд Symbolics / Variable / Convert to Partial Fraction (Символика / Переменная / Разложить на элементарные дроби или Преобразовать в частичные доли).

Таблица 5.8

− Рациональные дроби

Вариант

Выражения

Вариант

Выражения

x 2 + 1

x5 − x3 − x2

2x 4

x(x 2 −1)

; 2)

+ x2 +1

x6 + 8

x2 −1

; 2)

x 2

; 2)

5x 2 − 4x +16

(x 2 −1)2

(x −1)2 (x +1)

+ 4

(x2 − x +1)2 (x − 3)

102

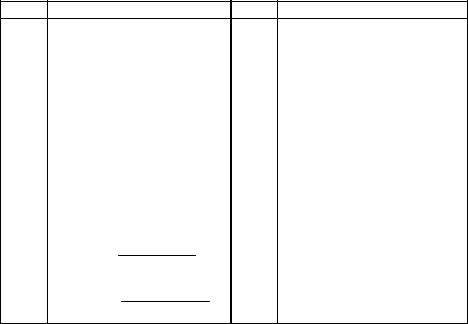
Окончание таблицы 5.8

Вариант

Выражения

Вариант

Выражения

	1)		x6 − x2 +1				;							1)		1		;
5	1)		(x −1)3				;						11	1)	x3 +1			;
5			3x3 +15x + 6										11								2
	2)		3x3 +15x + 6											2)							2
															x	4	+ 2x		3	+ 2x					2		+ 2x +1
			x4 + x3 + 3x 2 + 2x + 2													4			3						2
			x4 + x3 + 3x 2 + 2x + 2
6	1)		x 2 +1							; 2)		x4 +1	12	1)			2x + 3							; 2)				2x3 + 4x
6	1)	(x 2 + x +1)2								; 2)		x3 (x 2 +1)2	12	1)	(x − 3)(x + 2)									; 2)				x4 + x 2 + 4
7	1)	1		; 2)					3x 2		− 3		13	1)		1		; 2)										2
7	1)		x3 −1	; 2)		x3 − 3x +1							13	1)	x 4 −1			; 2)				(x −1)(x − 2)(x − 3)
8	1)	1			; 2)						2		14	1)			1						; 2)				6x2 − x + 1
8	1)		x4 − x 2		; 2)				x2 (x −1)(x − 2)				14	1)	x4 + x 2 +1								; 2)					x3 − x
	1)	1		; 2)						x 2 −1				1)		x4 +1					; 2)							3x
9							(2x +1)(x2 +1)						15

			x5 −1												x(x2 +1)2											(x − 3)(2x +1)
		1								3x 2 − 2						x + 1												x 2 − 2
10	1)			; 2)				(x2 + x +1)(x +1)					16	1)							; 2)

			x5 − x												x(x −1)3										(3x +1)(x +1)

11Выполнить задание 8.

Задание 8. Для указанных матриц (таблица 5.9) выполнить команды меню Symbolics / Matrix (Символика / Матрица, Матричные операции): Transpose (Транспонировать, получить транспонированную матрицу), Invert (Инвертиро- вать, создать обратную матрицу), Determinant (Детерминант, вычислить опре- делитель матрицы).

Для выполнения указанных операций матрица выделяется синим управляю- щим курсором целиком.

Таблица 5.9 − Матрицы

Вариант

Матрицы

Вариант

Матрицы

1 2xö

æ x

yö

æa 1 1ö

æ1 a

; 2)

5x x

1 b 1÷

1) ç

è2 z ø

èb

cø

æa

æ x 2

x 2 ö

çæ 1 2

æa 1 0ö

; 2)

÷ö

; 2)

1) ç

1 b 1

3 x 2x÷

èp

è x

x ø

103

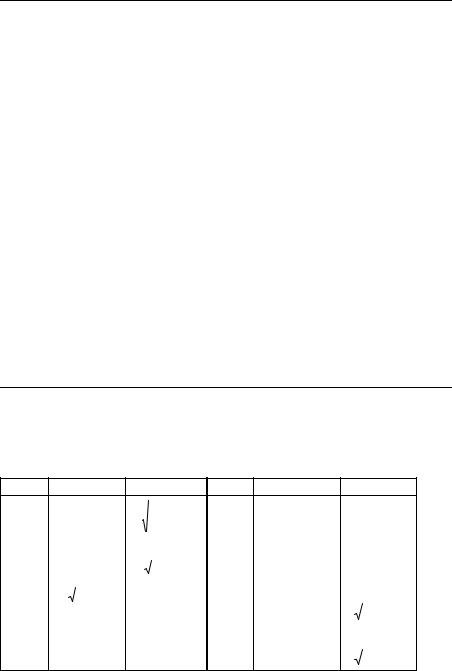
Окончание таблицы 5.9

Вариант

Матрицы

æ x

yö

æ1- a

÷ ; 2)

1-b

è z

1- c

æ 1

x ö

æa +1

1ö

b +1 1

1) ç

÷ ; 2)

è y

-1ø

æ x

yö

æ1- a

÷ ; 2)

1-b

è z

1- c

æ a

-bö

æ x

x ö

; 2)

- x÷

è- a

a ø

çæ x

æa-1

1 ö

x 2

÷ö ; 2)ç

1 b-1 1

- x

è x

c -1ø

æa 2

æ x

1 2xö

÷ ; 2)

3 ÷

è c

4 ø

Вариант

Матрицы

çæ1 x ÷ö

æ 1

-bö

; 2)

-c

è2

-a

æ x

y ö

æ a

0ö

÷ ; 2)

ç-1

1÷

è z

wø

-1

è 0

cø

çæ1 y ÷ö

æ0

1 1ö

; 2)

è z

wø

æ 1

a2 ö

æ 1

- yö

1)ç

÷; 2)

ç-x

1 ÷

è-1

-1

æa

a 2 ö

æ1

- xö

÷ ; 2)

ç2

y ÷

èb

- y

èx

æ1

2ö

æ1

c ö

÷ ; 2)

ç c

a÷

è3

xø

èa

1ø

12Выполнить задание 9.

Задание 9. Вычислить в символьном виде сумму ряда и неопределенный ин- теграл (таблица 5.10). Определить m в виде константы и символа ∞.

Таблица 5.10 − Суммы и интегралы

Вариант

Сумма

Интеграл

sin12

òx

1- x2 dx

n=0

1+ x

cos 2

- 4)dx

(2n + 1)

n=0

16 + x 4

ò e x

sin 2

xdx

n=1

å sin2

ò x2

sin3

xdx

n=2

−1

Вариант

Сумма

Интеграл

n=1

1 + n

2x + 1

22n +1 2

(x +1)dx

n (n +1)

n=1

sin xdx

(4n

−1)

cos

n=1

å cos12

cos xdx

n=2

n −1

cos

104

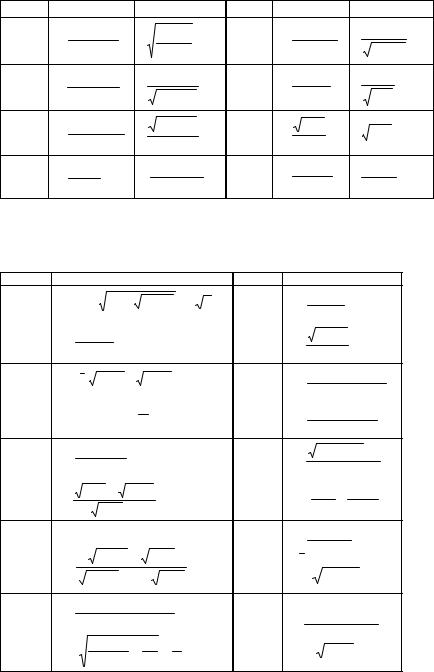
Окончание таблицы 5.10

Вариант

Сумма

Интеграл

Вариант

Сумма

Интеграл

sin1

sin

x dx

2n +1

sin x

n(n

+ 5)

+1)

cos 2x

n 1

cos

n 1

(-1)n sin1

x3dx

n(n

+ 9)

2x − x

(n +1)

tg x

n=1

(−1)2

cos1

a + bx

sin2

tg xdx

n=3

− 4

n=1

(−1)n

sin x

n -1

cos 3x

−1

sin(x

− α)

(n +1)

sin

n=2

n=1

13Выполнить задание 10.

Задание 10. Вычислить пределы (таблица 5.11).

Таблица 5.11 − Пределы

Вариант

Пределы

Вариант

Пределы

lim x

+1 - x

;

lim

ln x -1

;

x - e

x →+∞

x→e

lim lg x -1

+ n

lim

x→10

x -10

n→∞

n + 2

+1 − 3

−1);

lim tgx -1+ cos 3x ;

limx3

x→∞

p ö

x→0

e x - e−x

lim

ln cos

− e

− x

− 2x

ç n

lim

n → ∞

n ø

x − sin x

x→0

lim n2

+ n +2

1 ;

lim

1+ x + x2 -1 ;

n→∞

(n −1)

x→0

1+ x −

1+ x

lim

limç

1- x

- x

x→0

1+ x −1

x→1

lim(arcsin(x - a)ctg(x - a));

lim

ln tg x

;

x→a

1− ctg x

1+ 3x −

+ x

x→ π

lim

1+ 2x + x − 5

1+ x

lim (

x 2

+ 1 − x)

x →0

lim (n +1)(n + 2)(n + 3) ;

x → ∞

lim

-1+ x3 sin

n→∞

+ n2 +1

2 ;

1 ö

x→0

lim x(

+1 − x)

lim

x(x - 1)

x→ 0

x→+∞

105

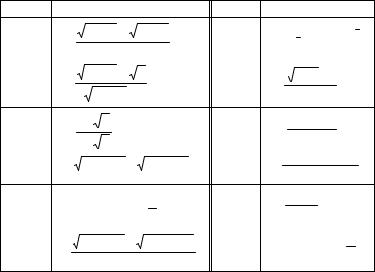
Окончание таблицы 5.11

Вариант

Пределы

Вариант

Пределы

1- 2x - 3 1+ 3x

lim

;

- (x

ö3

;

limx

x→0

x + x

ç x

- 1)÷

→ ∞

+1 +

3 1+ x -1

lim

n→∞ 4 n2 + n - n

x→0

lim 1+ 3

x ;

lim ln(e x

+1) ;

x→−1 1+ 5

x→+∞

lim(

x2 + x +1 -

x2 - x +1)

lim

xecos x

x→∞

n →∞

1- sin x - cos x

öö

;

lim

sin 3x

;

limç x - x

lnç1

÷÷

x→π

tg 5x

x→∞ è

øø

æ p

p ö

3+ x + x

9 - 2x + x

lim

lim n ln tgç

x2 -3x + 2

n→∞

è 4 n ø

x→0

14Задать оператор пользователя.

15Распечатать лабораторную работу. Завершить работу с Mathcad.

Контрольные вопросы

1Назовите способы выполнения символьных операций в Mathcad.

2Перечислите особенности подготовки и выполнения символьных преобразований.

3Какие параметры определяет стиль представления результатов символьных пре- образований и как он задается?

4Перечислите символьные операции с выделенными выражениями.

5Перечислите символьные операции с выделенными переменными.

6Перечислите символьные операции с выделенными матрицами.

7Перечислите символьные операции преобразования.

8В каких случаях результат символьных преобразований помещается в буфер обмена?

9Каким образом можно вычислить предел в Mathcad?

10Для чего необходимо задание операторов пользователя? Как задать оператор поль- зователя?

106

СПИСОК РЕКОМЕНДУЕМОЙ И ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1Дьяконов, В. П. Энциклопедия Mathcad 2001i и Mathcad 11 / В. П. Дьяконов. −

М. : СОЛОН-Пресс, 2004. −832 с.

2Кирьянов, Д. В. Самоучитель Mathcad 13 / Д. В. Кирьянов. − СПб. : БХВ-Петербург, 2006. − 560 с.

3Черняк, А. А. Высшая математика на базе Mathcad. Общий курс / А. А. Черняк, Ж. А. Черняк, Ю. А. Доманова. − СПб. : БХВ-Петербург, 2004. − 608 с.

4Очков, В. Ф. Физические и экономические величины в Mathcad и Maple / В. Ф. Очков. − М. : Финансы и статистика, 2002. − 192 с.

5Каплан, А. В. Решение экономических задач на компьютере / А. В. Каплан [и др.].

−М. : ДМК Пресс; СПб. : Питер, 2004. −600 с.

6Салманов, О. Н. Математическая экономика с применением Mathcad и Excel / О. Н. Салманов. − СПб. : БХВ-Петербург, 2003 −464 с.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1111

Соседние файлы в предмете Информатика

#
05.07.202262.09 Кб4Faylovy_menedzher (1).docx
#
05.07.2022885.22 Кб35Mathcad_для_экономистов_Голдобина_2.pdf
#
05.07.202246.99 Кб1Osnovy_formatirovania_dokumentov_v (1).docx
#
05.07.202222.5 Кб4Trebovania_otchet.docx
#
05.07.202248.45 Кб4Среда программирования IDLE.docx
#
08.07.20223.45 Mб19шпоры инфа 1 семестр.docx