
Mathcad_для_экономистов_Голдобина_2
.pdf
éb1 ù êb ú
b = ê 2 ú − столбец свободных членов.
êê...úú ëbn û
Расширенная матрица системы содержит все коэффициенты системы, вклю-
чая и столбец свободных членов. Обозначим ее AR: |
|
||||
éa |
a |
... |
a |
b |
ù |
ê 11 |
12 |
|
1n |
1 |
ú |
AR = êa21 |
a22 |
... |
a2n |
b2 |
ú . |
ê ... ... |
... ... |
...ú |
|||
ê |
an2 |
... |
ann |
|
ú |
ëan1 |
bn û |
||||
Как известно, система линейных алгебраических уравнений имеет решение, если ее определитель отличен от 0: det(A) = A ¹ 0 . При этом ранг матрицы ко-
эффициентов при неизвестных системы равен рангу расширенной матрицы сис-
темы: rank(A) = rank(AR) .
Mathcad обладает широкими возможностями для решения систем линейных уравнений. В частности, решение можно осуществить с помощью блоков Given…find, Given…minerr. При этом начальное приближение неизвестным за- дается произвольно, а проверка не требуется. Вычислительные блоки в по- следних версиях Mathcad способны решать системы линейных уравнений, со- держащие до 400 неизвестных.
Решение систем линейных уравнений с помощью обратной матрицы
Рассмотрим систему линейных уравнений в матричном виде Ax = b. Умно- жим обе части данного матричного уравнения на обратную матрицу коэффици-
ентов при неизвестных системы A-1 слева: A−1 Ax = A−1b . Учитывая, что A−1 A = E , вектор-столбец решений системы можно искать в виде
x = A−1b .
Этот прием используется в Mathcad так:
1)задается матрица коэффициентов при неизвестных системы A;
2)задается столбец свободных членов b;
3)вводится формула для нахождения решения системы X := A−1b ;
4)выводится вектор решений системы X = .
Использование функции lsolve(A, b)
Пакет Mathcad имеет встроенную функцию lsolve(A, b),
возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при
71

неизвестных системы и столбец свободных членов. Порядок решения аналоги- чен приведенному в предыдущем пункте.
Использование матричной функции rref(A)
Реализовать широко известный метод решения систем линейных алгебраи- ческих уравнений путем последовательного исключения неизвестных (метод Гаусса) позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу AR систе- мы, то функции rref(AR) возвратит матрицу, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.
Аналитическое решение уравнений и систем уравнений
Используя пакет Mathcad для символьного, или аналитического (т. е. пред- ставленного в виде формул или полученного путем аналитических преобразо- ваний) решения уравнений, систем уравнений и неравенств, следует помнить,
что не каждое выражение разрешимо относительно выбранной переменной в аналитическом виде.
Символьный процессор возвращает результат решения в виде выражения (численного или символьного), которое вполне можно использовать в дальней- ших вычислениях. Если решений имеется несколько, то возвращается содержа- щий их массив (например, вектор-столбец).
Использование стандартных функций
Для аналитического решения уравнений, систем уравнений и неравенств применимы те же функции и блоки, что и при численном решении. А именно, функция root(f(x1, x2, ...), xi, [a, b]) – для решения уравнений, правая часть кото- рых равна 0; вычислительные блоки Given…find и Given…minerr – для решения уравнений, неравенств и систем. При этом начальное приближение переменным не задается, а для вывода результата используется оператор символьного выво-
да (Evaluate Symbolically) «→» (комбинация клавиш Ctrl + .).
Пример 4.2. Решить уравнение x2 - 2 = 5bx +1 . ax
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = 0 . |
|
|
|
|
|
|
|
|
|||||||
1-й |
способ. |
Преобразуем |
уравнение |
к |
|
виду |
В |
рабочем |
поле |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
æ x 2 - 2 |
|
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Mathcad |
набираем |
rootç |
|
|
|
- 5bx -1, x÷ и нажимаем комбинацию клавиш |
||||||||||||||||||||||||||
ax |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ctrl + . для получения результата в символьном виде: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
é |
|
|
é |
|
|
|
|
|
|
1ù |
|
|
é |
|
|
|
|
|
1 ù ù |
|
||||
æ 2 |
|
|
|
ö |
|
ê |
|
|
ê |
|
( |
|
|
|
) |
|
ú |
|
|
ê |
( |
|
|
|
) |
|
ú |
ú |
|
|||
2 |
|
|
|
1 |
|
2 |
|
|
2 |
1 |
2 |
|
|
2 |
|
|||||||||||||||||
ç |
x |
− |
|
÷ |
|
ê |
|
ê |
|
|
|
ú |
|
ê |
|
|
|
ú |
ú |
|
||||||||||||
|
|
|
|
|
→ |
|
|
|
|
−a + |
|
+ 8 − |
|
|
|
|
|
ë−a − |
|
+ |
8 − 40b a |
|
|
|
||||||||
rootè |
|
a x |
|
|
− 5 b x − 1,xø |
ë 2(−1 + 5b a) |
ë |
a |
|
40b a |
|
|
û 2(−1 + 5b a) |
a |
|
|
|
û |
û |
. |
||||||||||||
72

2-й способ. Записываем ключевое слово Given. Ниже набираем уравнение с использованием логического знака равенства, которое вводится сочетанием кла- виш Ctrl + =. Для получения результата вводим с клавиатуры или из списка Insert Function (Вставка функции) категории Solving (Решение) функцию find(x), набираем символьный знак вывода:
Given |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 − 2 |
|
|
5 b x + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
é |
|
|
é |
|
|
|
1 ù |
|
|
|
é |
|
|
|
1 |
ù ù |
||
|
|
|
|
|
ê |
|
|
ê |
|
|
|
|
ú |
|
|
|
ê |
|
|
|
|
ú |
ú |
|
|
|
|
|
|
1 |
|
2 |
|
2 |
|
|
1 |
2 |
|
|
2 |
||||||
|
|
|
|
|
|
|
ê |
|
|
|
ú |
|
|
ê |
|
|
|
ú |
|
||||
Find (x) → |
ê |
|
|
ë−a + |
(a |
|
+ 8 − 40b a) |
|
û |
|
|
|
ë−a − (a |
|
+ 8 |
− 40b a) |
|
û |
ú |
||||
|
|
|
|
(−2 |
+ |
10b a) |
|
|
|||||||||||||||
|
|
|
|
|
ë (−2 + 10b a) |
|
|
|
|
|
|
|
|
|
|
|
|
û |
|||||
3-й способ. Уравнение решается аналогично предыдущему случаю, только вместо функции find(x) используется minerr(x).
ìax + 3y = 3;
Пример 4.3. Решить систему уравнений í ( )
î6x - b + p y = 1.
Решение.
1-й способ. Записываем слово Given. Ниже набираем все уравнения, входя- щие в систему, с использованием логического знака равенства. Записываем функцию find. Для вывода результата набираем символьный знак вывода →:
Given |
|
|
|
|
|
|
|
|
|
|
||
a x + 3y |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
6x − (b + π)y |
|
|
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
é |
|
|
( |
b + π + |
) |
|
ù |
||
|
|
|
3 |
|
|
1 |
|
|||||
Find (x, y) → |
ê |
|
(18 + b a + π a) |
ú |
||||||||
ê |
|
|
|
(−a + 18) |
|
|
ú |
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
ëê |
|
|
|
ûú |
|||||
|
|
|
|
|
(18 + b a + π a) |
|||||||
2-й способ решения аналогичен предыдущему, только вместо функции find используем minerr.
Применение команды Solve главного меню Symbolics и одноименной директивы палитры Symbolic
Для аналитического решения уравнений или неравенств в пакете Mathcad можно использовать последовательность команд главного меню. При этом ре- комендуется следующий порядок действий:
1 Вводится уравнение или неравенство с использованием логического знака
равенства или иных операций палитры математических инструментов Boolean
73

(Логические). Если уравнение приведено к виду f (x) = 0 , то можно задать его левую часть, и выражение будет приравнено к нулю автоматически.
2Искомая переменная выделяется синим управляющим курсором.
3Выполняется последовательность команд главного меню Symbolics / Variable / Solve (Символика / Переменная / Решение).
Пример 4.4. Решить уравнение x3 − 3x = 1 . Решение.
x3 − 3x 1
é |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ù |
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ê |
|
|
|
|
|
|
|
|
|
2 |
(4 |
+ 4 × i 3) |
|
|
|
+ |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
||||||||
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4 + 4 × i |
|
) 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|||||||||
ê |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
é |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
ù ú |
|
|
|
|
|||||||||||||||||
ê |
−1 (4 + 4 × i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú ú |
|
æ |
1.879 ö |
||||||||||
|
) 3 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) 3 − |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
ê |
|
|
|
|
|
1 |
|
|
|
+ 1 i |
|
|
|
1 (4 + 4 × i |
|
|
2 |
|
|
|
|
|
|
ú ú |
|
ç |
|
÷ |
||||||||||||||||||||||||||
3 |
|
|
|
|
3ê |
|
|
= |
−1.532 |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
ê 4 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
ê 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ú ú |
ç |
÷ |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú ú |
|
è |
−0.347ø |
||||||||
|
|
|
|
|
|
|
( |
|
|
|
|
|
) 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
) 3 |
|
|||||||||||||||
ê |
|
|
|
|
|
|
|
|
4 |
+ 4 |
× i 3 |
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
+ 4 × i 3 |
û ú |
|
|
|
|
||||||||||||||||
ê |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
é |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
ù |
ú |
|
|
|
|
||||||||||||||||
ê |
−1 ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
ú |
|
|
|
|
||||||
|
|
|
) 3 |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
1 |
( |
|
|
|
|
|
|
|
) 3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|
||||||||||||||||||||
ê |
4 |
|
|
− |
|
|
|
|
|
|
|
|
− |
|
|
|
|
4 |
− |
|
|
|
|
|
|
|
|
ú |
|
|
|
|
||||||||||||||||||||||
4 |
+ 4 × i 3 |
|
|
|
|
|
|
|
|
2 |
i 3 |
2 |
+ 4 × i 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
ê |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
ú |
ú |
|
|
|
|
||||||||||||||||||
ê |
|
|
|
|
|
|
|
( |
4 |
+ 4 |
|
|
) 3 |
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
4 |
|
|
) 3 |
ú |
ú |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
ë |
|
|
|
|
|
|
|
|
× i 3 |
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 4 × i 3 |
û û |
|
|
|
|
|||||||||||||||||||
После упрощения результата (оператор «=») получим вектор решений, пред- ставленных в виде десятичных дробей.
Специальная директива solve (Решить) палитры математических инструмен- тов Symbolic (Символические или Ключевые слова) позволяет решать не только уравнения, но и системы уравнений и неравенств (рисунок 4.1).
Рисунок 4.1 − Директивы палитры Symbolic
Для того чтобы найти с его помощью корни уравнения, выполняется сле- дующая последовательность действий:
74
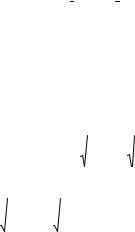
1 Вводится оператор solve (Решить) при помощи одноименной директивы палитры Symbolic:
 solve ,
solve , ®
®
2 В левом местозаполнителе задается уравнение с использованием логиче- ского равенства. Если уравнение приведено к стандартному виду f (x) = 0 , то
достаточно определить только его левую часть. Слева можно ввести имя встро- енной или ранее определенной функции пользователя. В этом случае будут найдены выражения, определяющие ее нули.
3 В правом местозаполнителе указывается переменная, относительно кото- рой должно быть решено уравнение.
Пример 4.5. Решить уравнение |
|
|
2 |
|
|
- |
|
x + 2 |
|
= |
|
7 |
. |
|||||||||
x + 2 |
2 |
12 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
7 |
|
|
|
-7 |
||||||||||
|
2 |
|
- |
|
x + 2 |
- |
solve , x |
® |
||||||||||||||
|
|
x + |
|
2 |
|
|
12 |
8 . |
||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Для того чтобы получить аналитическое решение системы уравнений с по- мощью директивы solve (Решить):
1)вводится директива solve (Решить) с палитры Symbolic;
2)создается вектор-столбец (например, сочетанием клавиш Ctrl + M), ко- личество строк в котором равно числу уравнений системы;
3)в каждое знакоместо вектора вводится одно уравнение системы с исполь- зованием логического равенства;
4)имена искомых переменных перечисляются через запятую в правом зна- коместе.
|
Пример 4.6. Решить систему уравнений íìax |
|
2- y = a; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
î2x |
|
+ ay = 1. |
|
|
|
|
|
|
|
|
|||||||||
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
é |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
é |
|
|
|
|
|
|
|
|
|
|
|
1 |
ù ù |
|||
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
ú ú |
||
|
|
|
|
|
|
|
|
|
2 |
|
1 ( |
4 |
|
2 |
|
)2 |
|
|
−1 |
|
2 |
|
1 ( |
4 |
|
2 |
)2 |
||||||||||
|
|
|
|
|
|
ê −1 |
|
|
|
|
|
|
ê |
|
|
|
ú ú |
||||||||||||||||||||
æ |
a x − y |
|
|
a ö |
ê |
|
|
a |
|
+ |
4 a |
|
+ 8a |
+ |
8 |
|
|
aë |
|
|
a |
|
+ |
|
a |
|
+ 8a |
+ 8 |
|
− 1û ú |
|||||||
|
|
4 |
|
|
|
4 |
|
4 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
ç |
2x2 + a y |
|
|
÷ solve , x, y |
→ ê |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
é |
|
|
|
|
|
|
|
|
|
|
|
1 |
ù |
ú |
|
è |
|
1 ø |
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
ê |
−1 |
|
2 |
|
1 ( |
4 |
|
2 |
|
)2 |
|
|
|
ê |
−1 |
|
2 |
|
1 ( 4 |
|
2 |
)2 |
ú |
ú |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
ú |
||||||||||||||||||||
|
|
|
|
|
|
ê |
|
|
a |
|
− |
|
a |
|
+ 8a |
|
+ |
8 |
|
|
|
a |
|
|
|
a |
|
− |
|
a |
|
+ 8a |
|
+ 8 |
|
− 1 |
ú |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
ë |
4 |
|
|
4 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
ë |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
û û |
||||||
Примечание – Символьный процессор Mathcad способен аналогичным образом об- рабатывать самые простые неравенства, как правило, с числовыми коэффициентами.
75

Порядок выполнения лабораторной работы
1 Загрузить Mathcad. Сохранить новый документ с именем ФИОСтудента4. 2 Ввести в поле документа данные о студенте и выполняемой работе.
3 Выполнить задание 1.
Задание 1. Отделить корень или корни уравнения (таблица 4.1) графически.
Уточнить один или несколько корней уравнения с помощью: |
|
|
|
|
|
|||||||||||||||||||||||||||||||
∙ функции root, двумя способами; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
∙ |
вычислительных блоков Given…find и Given…minerr. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Сделать проверку. Исследовать влияние системной переменной TOL на точ- |
||||||||||||||||||||||||||||||||||||
ность найденного решения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Таблица 4.1 − Нелинейные уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вариант |
|
|
|
|
|
|
|
|
|
|
Уравнения |
Вариант |
|
|
|
|
|
|
Уравнения |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1) |
|
x3 − 0,1tg2 |
|
x = 1,5 ; |
|
|
ctg(x +1)− 3 |
|
|
|
= 0 ; |
|
||||||||||||||||||||||
1 |
9 |
1) |
|
x |
|
|||||||||||||||||||||||||||||||
|
2) |
(x − 4)cos x = 1 |
2) |
|
x2 cos 0,5x = −2 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
1) |
|
x3 − 0,1tg2 |
|
x = 5,1 ; |
|
1) |
cos 2 (5x)+ 5x = 14 ; |
|
||||||||||||||||||||||||||
2 |
|
2) |
|
|
cos 2 x |
= 1 |
10 |
2) |
|
x + sin2 |
x |
= −0,5x |
|
|||||||||||||||||||||||
|
|
|
ln( |
|
x |
|
+1,5) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2x |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3 |
|
1) |
|
x3 cos(x)= 2 ; |
11 |
1) |
log32 (x + 2)+ 2x = 0 ; |
|
||||||||||||||||||||||||||||
|
2) |
ctg2 (x +1)− x =1,8 |
2) |
(x +12)arctg(0,6x) = 1 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
4 |
|
1) |
(x +1)arcctg(6x) = 0,3 ; |
12 |
1) |
log22 (x +1)−1 = x ; |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2) |
3 3x + cos x = 2 |
2) |
ctg3 (x + |
|
x )= x |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
1) |
e x − cos3 3x = 0,8 ; |
|
1) |
ln(x +1)− |
|
|
2 |
|
|
|
= 1,5 ; |
|
||||||||||||||||||||||
5 |
|
2) |
|
|
|
|
|
x |
|
= (0,5x)2 |
13 |
x |
+ |
2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
cos 3 x + 2 |
|
2) |
0,2x + sin 3 (3x +1) = 2 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
6 |
|
1) |
(x +1)2 lg(3x + 2) = 2 ; |
14 |
1) |
esin 2x = sin 2 |
x +1 ; |
|
||||||||||||||||||||||||||||
|
2) |
e2x − cos 3 x = 0,1 |
2) |
log52 (x +1,1)+ x = 0 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
1) |
3x−2 |
− x3 = arcctg(x); |
|
1) |
2x − arccos x =1 ; |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
e |
x |
= 90 |
15 |
2) |
|
|
|
3 sin x |
= 0,7 |
|
|
|
|
|||||||||||||||
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
sin2 |
|
|
2x +1 |
|
|
|
x2 |
+1 |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
8 |
|
1) |
e x − lg3 (x) = 6 ; |
16 |
1) |
e3− x |
+ sin2 (x) =1,1; |
|
||||||||||||||||||||||||||||
|
2) |
sin2 x ( |
|
x |
|
+ 2)= 3,9x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2) |
3 x + x 2 |
= −ex |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
76 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Пример выполнения задания 1
-p ö = - ( + )=
1)2,1sin 2 ç x ÷ 0,4x 2 1; 2) x log2 x 1 2 .
è4 ø
1)Преобразуем первое уравнение к виду f(x) = 0 и определим функцию пользователя f(x). Для построения графика создадим ряд значений аргумента x в виде ранжированной переменной с мелким шагом:
|
æ |
π ö2 |
2 |
|
f(x) := 2.1sin |
èx − |
4 ø |
− 0.4x |
+ 1 |
x:= −10, −9.9.. 10
Вставим графическую область. В нижнем местозаполнителе укажем имя пе- ременной, а в среднем левом − функцию.
Отформатируем график в окне Formatting Currently Selected X-Y Plot
(Форматирование текущего графика): установим пересечение координатных осей, вспомогательные линии. Откорректируем видимую область значений функции f(x) в левом верхнем и нижнем местозаполнителях таким образом, что- бы четко определялись точки пересечения с осью абсцисс.
С этой же целью можно использовать масштабирование (X-Y Zoom), трас- сировку (X-Y Trace) и установку меток по осям в следующем порядке:
·увеличить область графика, в которой наблюдается пересечение графика функции с остью абсцисс, с помощью окна X-Y Zoom (Масштабирование), вы- зываемого командами Format / Graph / Zoom… (Формат / График / Масштаб);
·выбрать опцию отображения линий-меток по оси абсцисс. Для этого вы-
зывается окно форматирования графика и на вкладке X-Y Axes в списке X-Axis ставится флажок Show Markers (Отображать метки);
·с помощью окна X-Y Trace (Трассировка), вызываемого командами Format / Graph / Trace… (Формат / График / Трассировка…), отследить точку пересечения графика функции с осью абсцисс;
·вписать значение, отображаемое в строке X-Value (Значение X), в место- заполнитель одной из линий-меток и щелкнуть левой клавишей мыши вне об- ласти графика:
77
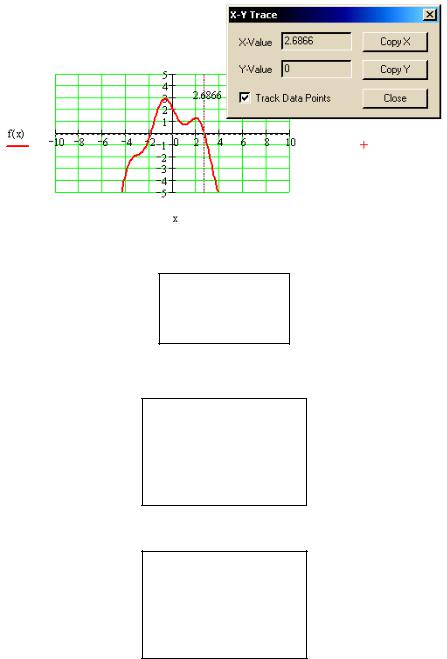
На графике видно, что один из корней уравнения расположен на отрезке [2; 4]. Уточним его с помощью функции root и сделаем проверку:
x1 := root (f(x) , x, 2, 4) x1 = 2.68422
f(x1) = 0
Проверка показывает, что корень найден с точностью около 10-15.
Уточним второй корень, предварительно указав его начальное приближение
x0:
x0:= −2 TOL := 0.01 x2:= root(f(x0), x0)
x2 = −1.88877
f(x2) = −6.043× 10− 4
Оценим влияние системной переменной TOL на точность найденного корня. Для этого уменьшим TOL:
x0:= −2 TOL:= 0.0001
x2:= root(f(x0), x0)
x2 = −1.88858
f(x2) = −5.953× 10− 7
Корень найден с точностью менее 10-6. При меньшем значении TOL получен более точный корень.
78
Уточним один из корней с помощью блока Given…find, сделаем проверку: |
|||||||||||||
|
|
x0:= −2 |
TOL := 0.0001 |
|
|
|
|
||||||
|
|
Given |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
π ö2 |
|
|
2 |
|
|
|
|
|
|
|
2.1sin |
èx0 |
− 4 ø |
|
0.4x0 |
− 1 |
|
|
|
|
||
|
|
x2:= Find(x0) |
|
|
|
|
|
|
|
|
|||
|
|
x2 = −1.88858 |
|
|
|
|
|
|
|
|
|||
|
|
f(x2) = 3.398× 10− 7 |
|
|
|
|
|
|
|||||
Аналогично уточним корень с помощью блока Given…minerr. |
|
|
|||||||||||
2) Приведем |
уравнение |
x log2 (x +1)= 2 |
к |
виду |
f(x) = g(x), |
где |
f (x) = |
||||||
= log 2 (x +1), g(x) = 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
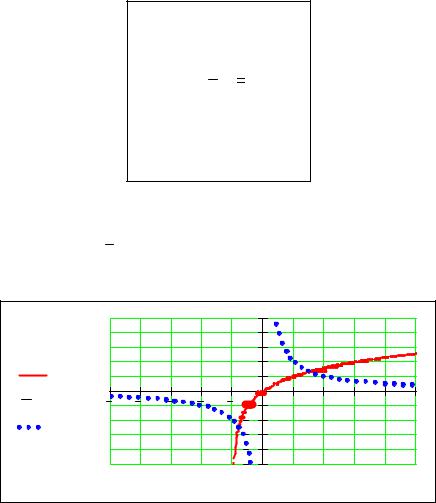
Для наглядности изобразим графики этих функций в одной плоскости, напе- |
|||||||||||||
чатав их в левом среднем местозаполнителе через запятую. |
|
|
|
||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
log(x+ 1, 2) |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
5 |
4 |
|
3 |
2 |
1 |
|
0 |
1 |
2 |
3 |
4 |
5 |
|
x |
|
1 |
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
Очевидно, что первый корень уравнения x1 ≈ −1, а второй расположен на |
|||||||||||||
промежутке [1; 2]. Дальнейшее уточнение корней проводится с помощью функ- |
|||||||||||||
ции root или блоков Given…find, Given…minerr. |
|
|
|
|
|
|
|||||||
4 Выполнить задание 2. |
|
|
|
|
|
|
|
|
|
|
|
||
Задание 2. Решить полиномиальное уравнение (таблица 4.2). Построить |
|||||||||||||
график полинома и отобразить в той же координатной плоскости полученные |
|||||||||||||
корни. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
79 |
|
|
|
|
|
|
|
|

Таблица 4.2 − Полиномиальные уравнения
Вариант |
|
Уравнение |
Вариант |
|
Уравнение |
|
|
|
|
|
|
||
1 |
x4 − 2x3 − 6x 2 + 2x + 2,5 = 0 |
9 |
x4 + 2,2x3 + 5,6x2 −1 = 0 |
|
||
|
|
|
|
|
|
|
2 |
x5 −2,5x4 −5x3 +1,9x2 −17x +1= 0 |
10 |
x4 |
− 4,2x3 − 3x + 2,3 = 0 |
|
|
|
|
|
|
|
||
3 |
x4 − 2,2x3 − 5,1x2 + 3x +1 = 0 |
11 |
x4 +16x3 − 2x2 +1 = 0 |
|
||
|
|
|
|
|
|
|
4 |
x4 |
−14x3 + 3,4x 2 + x − 4 = 0 |
12 |
x5 |
−10,2x3 + 4,6x +1,2 = 0 |
|
5 |
x5 +3x4 −8x3 −7x2 +3,9x −11= 0 |
13 |
x4 |
+ x3 − 4,9x 2 − 3,8x +1 = 0 |
|
|
|
|
|
|
|
|
|
6 |
x4 |
− 6,9x3 + x2 −12 = 0 |
14 |
x4 |
−11x3 − 54x2 + 86 = 0 |
|
|
|
|
|
|
|
|
7 |
x3 |
− 7x2 + 20,3x −11,8 = 0 |
15 |
x5 |
+ 5,2x3 − 7,3x + 2 = 0 |
|
|
|
|
|
|
|
|
8 |
x3 |
− 33,2x 2 + 8x +10,1 = 0 |
16 |
x3 + 3,3x 2 − 4x −1,5 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Пример выполнения задания 2 |
|
|||
|
|
Решить уравнение 12x4 −14x3 |
− 3x2 − 5 = 0 . |
|
||
Зададим полином:
12x4 − 14x3 − 3x2 − 5 .
Установим синий управляющий курсор на переменную x и выполним после- довательность команд главного меню Symbolics / Polynomial Coefficients (Сим- волика / Полиномиальные коэффициенты). В результате получим вектор коэф-
фициентов полинома
æ −5 ö
ç÷
ç0 ÷
ç−3 ÷
ç−14 ÷÷
è 12 øç
Для удобства дальнейшей работы вырежем, например, кнопкой панели инструментов Standard (Стандартная) полученный вектор в буфер обмена. За- дадим переменную и присвоим ей значение вектора коэффициентов полинома,
вставив его из буфера обмена кнопкой  :
:
80
