
- •РОЗДІЛ 2
- •ГЕОМЕТРІЯ ЗЕМНОГО ЕЛІПСОЇДА
- •Рис. 2.1. Основні параметри еліпса.
- •Таблиця 2.1. Параметри еліпсоїдів
- •Рис. 2.2. Геометричний зміст координатних ліній на поверхні еліпсоїда
- •Рис. 2.3. Геометричне трактування широт: геодезичної, приведеної та геоцентричної.
- •Рис. 2.9. Диференціали дуг меридіана та паралелі.
- •На основі (2.60) отримаємо
- •РОЗДІЛ 4
- •РОЗВ’ЯЗУВАННЯ ГЕОДЕЗИЧНИХ ЗАДАЧ
- •Рис. 4.1. Великий геодезичний трикутник на поверхні еліпсоїда
- •Сферичний надлишок
- •Таблиця 4.1Допустимі вхідні дані для обчислення сферичного надлишку
- •Згідно теореми Лежандра, значення кутів плоского (лежандрового) трикутника буде
- •Позначивши
- •Пряма геодезична задача
- •Обернена геодезична задача.
- •Шляхом ділення рівнянь (4.19) на (4.18) дістанемо формулу для оберненого азимута
- •Для обчислення оберненого азимута необхідно розділити рівняння (4.13) на (4.15)
- •Часткові похідні для другої похідної будуть наступними
- •Часткова похідна
- •З врахуванням отриманих виразів та формули (4.28) остаточно отримаємо
- •Часткові похідні в цих залежностях можна знайти із рівнянь (2.32)
- •Для цього попередньо визначимо похідні двох функцій
- •Враховуючи, що
- •Після цього можна легко знайти часткові похідні, наприклад
- •Після підстановки похідних в попередні залежності, отримаємо
- •Рис.4.6. Геометричне трактування зміни геодезичних координат.
- •Вивід диференційних рівнянь Бесселя
- •Вираз (4.81) з врахуванням (4.77) буде дорівнювати
- •Інтегрування диференційних рівнянь Бесселя
- •З врахуванням (3.89) і (3.99) рівність (3.98) представимо в вигляді
- •Розв'язування прямої геодезичної задачі методом Рунге-Кутта 4-го порядку
- •Згідно формули (5.2) для масштабу m отримаємо
- •Із наведених співвідношень отримаємо диференційні рівняння
- •Остаточні значення коефіцієнтів рядів (5.20) мають наступний вигляд
- •Підставивши значення похідних у (5.22), отримаємо
- •Оскільки
- •Таблиця 5.1
- •Таблиця 5.2
- •Таблиця 5.3
- •Таблиця 5.4
- •Таблиця 5.5
- •Таблиця 5.6
- •Таблиця 5.7
- •Спосіб прямої інтерполяції
- •Спосіб інтерполювання з використанням гравіметричних даних
- •Висота виміряна

Тема 4. Розв'язування геодезичних задач
Здійснивши паралельне зміщення еліпсоїда в просторі разом з осями координат OXYZ , отримаємо додаткові зміни геодезичних координат. Зміняться на цей раз і прямокутні координати всіх точок (в результаті переносу початку координат) на величини dx, dy, dz.
Вказані зміщення (перехід від одної системи геодезичних координат до другої) можна проіллюструвати геометрично (рис. 4.6).
В загальному вигляді залежності між всіма вказаними змінами можна записати у вигляді системи диференційних рівнянь
|
|
X |
|
|
|
|
X |
|
|
|
|
X |
|
|
|
X |
|
X |
|
|
||||||||
dx |
|
|
da |
|
|
d |
|
|
|
dB |
|
|
dL |
|
|
dH, |
|
|||||||||||
a |
|
B |
L |
H |
|
|||||||||||||||||||||||
|
|
Y |
|
|
|
Y |
|
|
|
Y |
|
|
Y |
Y |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
dy |
|
|
|
da |
|
|
|
d |
|
|
|
dB |
|
|
dL |
|
|
dH, |
(4.49) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
a |
|
|
|
|
|
|
|
B |
|
|
L |
H |
|
|
||||||||||||
|
Z |
|
|
|
Z |
|
|
Z |
|
|
Z |
Z |
|
|
||||||||||||||
dz |
|
|
da |
|
|
d |
|
|
dB |
|
|
dL |
|
|
dH. |
|
|
|||||||||||
|
|
B |
|
|
|
|
|
|||||||||||||||||||||
|
|
a |
|
|
|
|
|
|
L |
H |
|
|
||||||||||||||||
Z H H0  P
P
 B
B O
O
B0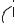
 X
X 
 X0
X0

|
d |
|
L |
L0 |
|
O |
||
|
Y Y0
Z0
P0
 dz
dz
 O0
O0
x 
 dy
dy
Проекція на площині екватора
Рис.4.6. Геометричне трактування зміни геодезичних координат.
Диференціали da, d та dB, dL, dH, dx,dy,dz представляють собою поправки до старих значень розмірів еліпсоїда (a,) і координат (B,L,H,X,Y,Z) довільної точки простору для отримання нових значень цих величин в другій системі геодезичних координат.
Часткові похідні в рівняннях ( 4.49) знаходимо шляхом диференціювання по відповідних змінних правих частин рівнянь (4.43). Раніше (див. п.4.5.2) нами вже отримано частину похідних (4.46). Аналогічним чином знаходять і інші похідні в (4.49).
Підставивши ці похідні в рівняння (4.49) та після відповідних перетворень, отримаємо остаточно
(M H )dB dx sin B cos L dy sin B sin L dz cos B
e2 |
N |
sin B cos Bda (N |
M |
) sin B cos Bd ; |
(4.50) |
||
|
1 e2 |
|
|||||
|
a |
|
|
|
|
||
(N H) cos BdL dx sin L dy cos L, |
(4.51) |
||||||
dH dx cos B cos L dy cos B sin L dz sin B |
a |
da N sin2 Bd . |
(4.52) |
||||
|
|||||||
|
|
|
|
|
N |
|
|
Тема 4. Розв'язування геодезичних задач
Умовою застосування вказаних диференційних формул є паралельність осей обертання та площин
початкових меридіанів обох еліпсоїдів.
Отримані вище формули можуть використовуватись для:
обчислення поправок в координати при переході до другої референцної системи координат (при відомих параметрах da, d , dx,dy,dz);
встановлення нової референцної системи координат (визначення вказаних п’яти невідомих параметрів).
Поправки da, d легко знайти, оскільки параметри еліпсоїдів, що застосовуються в практичних роботах,
переважно відомі. Що стосується інших трьох поправок, то вони визначаються наступним чином. За геодезичними координатами декількох пунктів Qi (i=1,2,...,n), відомими в двох системах координат, з
допомогою формул (4.50-4.52) можна визначити лінійний зсув dx,dy,dz одної системи відліку геодезичних координат відносно другої (така операція над координатами називається трансформуванням координат).
Вказану задачу можна сформулювати ще так. Дано координати окремих пунктів геодезичної мережі - (X,Y,Z), визначених з допомогою GNSS в деякій референцній системі, наприклад, WGS-84. Обчислити параметри трансформування для геодезичної мережі, у якій більшість пунктів є з відомими координатами B,L,H
в національній/місцевій референцній системі, причому деякі з них є спільними (відомі координати в обох референцних системах).
Розв'язування цієї задачі дістанемо за допомогою наступного алгоритму:
для спільних пунктів виконуємо перетворення декартових X,Y,Z, заданих в системі WGS-84 в
геодезичні B,L,H координати за допомогою формул ( 2.33));
визначаємо три параметри трансформування dx,dy,dz на основі формул (4.50-4.52 );
для пунктів GNSS, які не належать до спільних, використовуючи параметри трансформування,
знаходимо координати (B,L,H)REF в національній/місцевій референцній системі;
Нехай референцна система XYZ визначена в іншій системі X0Y0Z0 положенням початку координат dx,dy,dz
і кутами x, y, z, на які треба повернути систему XYZ відповідно навколо осей X, Y, Z, щоб ці осі стали паралельні відповідно осям X0,Y0, Z0.
В такій постановці декартові координати із одної системи в іншу будуть перетворюватись за формулами:
|
X |
|
|
|
X0 dx |
|
|||
|
|
|
|
|
|
|
dy |
|
|
Y |
|
R Y0 |
, |
(4.53) |
|||||
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
Z0 |
dz |
|
||
X0 |
|
|
dx |
|
|
X |
|
||
|
|
|
|
|
|
|
|
|
|
Y0 |
|
dy |
|
R' Y |
. |
(4.54) |
|||
|
|
|
|
|
|
|
|
|
|
Z0 |
|
|
dz |
|
|
Z |
|
||
При невеликих кутах повороту осей однієї системи координат відносно другої, що має місце в практиці,
матриця перетворення R має елементи
1
R z
y
- z |
|
y |
|
|
1 |
|
- x |
|
|
|
. |
(4.55) |
||
|
x |
1 |
|
|
|
|
|
|
У формулі (4.54) R' - транспонована матриця R, - масштабний множник. Трансформування координат
(4.54) називається ще трансформацією Гельмерта.
Формулу (4.54) можна представити і в такому виді:

Тема 4. Розв'язування геодезичних задач
dX X X 0 dx zY0 y Z0 ,
dY Y Y0 |
dy x Z0 |
z X 0 , |
(4.55) |
dZ Z Z0 dz y X 0 xY0 .
Кожен пункт Qi (i=1,2,...,n), координати якого відомі в двох референцних системах координат, утворює систему рівнянь (4.55). Шукані параметри зв’язку двох референцних систем координат можна обчислити з оцінкою точності, застосовуючи принцип найменших квадратів.
Розв'язування сформульованої вище задачі зв’язку двох референцних систем координат дістанемо за допомогою наступного алгоритму:
1) для спільних пунктів виконуємо перетворення геодезичних координат B,L,H в декартові X,Y,Z за допомогою формул (2.32);
2) визначаємо шість параметрів трансформування dx,dy,dz і x , y , z на основі формул (4.54) або
(4.55).
3)для пунктів загальноземної системи координат, які не належать до спільних, використовуючи параметри трансформування, знаходимо координати (X,Y,Z)REF в потрібній референцній системі;
4)перетворюємо обчислені в попередньому кроці координати із декартових (X,Y,Z)REF в геодезичні
(B,L,H)REF.
Точність переобчислених координат буде залежати:
від похибок формул, що застосовуються при обчисленнях;
від методів переходу виміряних елементів геодезичних мереж на поверхню референц-еліпсоїда;
від врівноважень, виконаних в геодезичних мережах кожної системи незалежно одна від другої.
4.6.Способи розв’язування головних геодезичних задач на поверхні еліпсоїда.
4.6.1. Розв’язування головних геодезичних задач методом із середніми аргументами (формули
Гаусса).
Пряма геодезична задача
Нехай на рис.4.7 крива Q1Q2 є геодезичною лінією між початковою точкою Q1 і кінцевою Q2.
P
 1
1
|
2 |
/ |
|
s |
|
B
1= c o
n s t
|
|
B |
|
|
|
|
= |
|
|
|
2 |
|
|
|
c |
|
|
|
o |
|
|
/2 |
n |
|
|
t |
|
|
s |
s |
|
|
|
||
0 |
B |
2 |
|
|
= |
|
|
|
|
m |
|
|
|
c |
|
|
s |
o |
|
|
|
s |
|
|
|
|
n |
|
|
|
t |
Рис.4.7. Геометрична схема розвязування головної геодезичної задачі методом Гусса.
Візьмемо точку Qo, розташовану на середині геодезичної лінії Q1Q2. Застосувавши формули (4.32) до кожної частини геодезичної лінії, отримаємо для широти

Тема 4. Розв'язування геодезичних задач
|
|
|
|
|
|
|
|
|
|
|
|
dB |
|
|
1 |
|
|
|
2 |
B |
|
|
s |
2 |
|
1 |
|
|
|
3 |
B |
|
|
|
s |
3 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
B1 Bo |
|
|
|
|
|
|
s / 2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
..., |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
|
ds |
|
|
|
|
8 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ds o |
|
2 |
|
|
|
|
|
o 4 |
6 |
|
|
|
|
|
o |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dB |
|
|
1 |
|
d |
2 |
B |
|
|
s |
2 |
|
|
1 |
|
d |
3 |
B |
|
|
s |
3 |
(4.56) |
||||||||||||||||||
|
|
|
|
|
B2 |
Bo |
|
s / 2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
ds |
|
|
|
4 |
6 |
|
ds |
|
|
|
|
8 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ds o |
|
|
|
|
o |
|
|
|
|
|
o |
|
|
|
|||||||||||||||||||||||||||
|
Віднявши в (4.56) перше рівняння від другого знаходимо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
B2 |
B1 |
dB |
|
d |
3 |
B |
|
|
|
s |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
s |
ds |
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
ds o |
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для різниць довгот та азимутів отримаємо аналогічно:
|
|
dL |
|
|
|
|
3 |
L |
|
|
s |
3 |
|
|
|
|
|
|||||||
L2 |
L1 |
s |
|
d |
|
|
|
|
|
.. |
|
|
|
|||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
ds |
|
|
24 |
|
|
|
||||||||||||||||
|
|
ds o |
|
|
|
o |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
dA |
|
|
|
|
|
|
|
3 |
A |
|
s |
3 |
|
||||||
A2 |
A1 |
|
|
|
|
s |
|
|
|
d |
|
|
|
|
|
|||||||||
180 |
|
|
|
|
|
|
|
|
3 |
|
|
|
... |
|||||||||||
|
|
ds |
|
|
24 |
|||||||||||||||||||
|
|
|
|
|
ds o |
|
|
|
|
|
|
o |
|
|||||||||||
де нульовий індекс при похідних показує, що вони повинні обчислюватись за Bo і Ao. Отримані вирази мають перевагу перед формулами (4.32): члени з парними степенями відсутні, а в інших членах коефіцієнти при них зменшились в декілька раз. Проте координати точки Qo(Bo, Lo, Ao), яка розташована посередині геодезичної лінії
Q1Q2, не будуть рівні середньому значенню координат цих точок (Bm, Lm,, Am).
Залежності між цими координатами можна отримати, якщо додати рівняння (4.56) і поділити на два:
B |
|
B |
|
|
1 |
d 2 B |
|
s |
2 |
. |
|
|
|
|
|
|
|
|
||||||||||
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.57) |
|||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
o |
|
8 |
|
ds |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Аналогічно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
L |
|
|
1 |
d |
2 L |
s |
2 |
|
|
|
|
||||||||||||
|
|
|
m |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
8 |
|
ds |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||||||
|
A |
A |
|
|
|
|
0 |
|
|
|
1 |
|
d 2 |
A |
s |
2 |
|
|||||||||||
|
180 |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
m |
|
|
0 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
ds |
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||
Як видно, ці залежності – малі величини другого порядку.
Приведені вище формули в загальному виді розв’язують поставлену задачу. Але оскільки ставиться за мету отримати різниці координат у функції Bm і Am, то потрібно встановити залежність між вказаними похідними. Вона виражається з допомогою наступного ряду Тейлора:
dB |
dB |
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
ds o |
|
ds m |
|
||
dB
ds m
B
|
|
|
|
|
dB |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
B |
o |
B |
m |
|
ds m |
A A . |
|||
|
|||||||||
|
|
|
|
A |
|
o |
m |
||
|
|
|
|
|
|
|
|
|
|
Часткові похідні, що входять в дану формулу дорівнюють:
dB |
|
|
|
cos |
Am |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ds |
|
M m |
|
|
|
|
|
|
|
|
||||
|
m |
|
|
|
3 N |
1 |
|
2 |
tm |
cos |
Am , |
|||
|
|
|
|
|
|
|
|
m |
|
|||||
|
B |
|
|
B |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dB |
|
|
|
cos |
Am |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ds |
|
M m |
|
|
|
|
|
|
|
|
||||
|
m |
|
|
|
M |
1 |
sin Am . |
|
||||||
|
A |
|
|
A |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
З похибкою на малі величини четвертого порядку, остаточно отримаємо

Тема 4. Розв'язування геодезичних задач
|
|
|
|
|
1 |
|
s2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s cos Am |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
B2 |
B1 |
|
|
24 |
|
Nm |
|
|
|
|
|
|
|
|
|||||
|
|
sin |
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|||||
M m |
2 |
|
|
|
2 m |
) |
|
|
|
||||||||||
|
|
|
|
|
|
Am (2 3tm |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
cos2 A (t |
|
1 |
|
4t |
2 |
|
||||
|
|
|
|
|
3 |
|
2 |
2 |
2 |
m |
|||||||||
|
|
|
|
|
|
m |
|
m |
m |
|
|
|
m |
|
m |
||||
а з похибкою на величину третього порядку можна записати:
, (4.58)
2 )
|
|
|
|
B |
2 |
B |
b |
s cos Am |
, |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
|
M m |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
L |
2 |
L |
l |
|
s sin Am |
, |
|
|
|
|
(4.59) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
|
N m cos Bm |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
A |
A 180o |
a |
|
|
|
s sin Am |
sin B |
m |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
N m cos Bm |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Використавши вирази (4.59) для перетворення поправочних членів у формулі (4.58) і не приймаючи до |
||||||||||||||||||||||
уваги члени |
s3 |
|
2 |
і менше, отримаємо для різниці широт остаточно: |
|
|
||||||||||||||||
R3 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
s cos Am |
1 |
l 2 |
|
|
a 2 |
. |
|
(4.60) |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
M m |
|
|
12 |
|
24 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Для різниці довгот та азимутів формули отримуються аналогічним чином. Запишемо ці формули в
кінцевому виді |
|
|
|
|
|
|
|
l |
s sin Am |
1 |
b2 |
|
a 2 |
, |
(4.61) |
|
|
|
|||||
|
|
|
24 |
24 |
|
|
|
|
N m cos Bm |
|
|
||||
a |
s sin Am |
sin B |
1 |
b2 |
|
a 2 |
|
l 2 |
. |
(4.62) |
|
|
|
|
|||||||
|
Nm cos Bm |
|
m |
12 |
24 |
12 |
|
|
||
|
|
|
|
|
||||||
Наведені скорочені формули для різниць широт, довгот та азимутів відрізняються від повних формул типу (4.58), які точні до величин четвертого порядку включно, лише на відкинуті малі величини порядку
s3 2 .
R3
В формулах (4.60)-(4.62) величини b,l,a – функції середньої широти Bm і середнього азимута Am, які невідомі. Невідомі також і аргументи b і l в поправочних членах вказаних формул. Тому пряма геодезична задача розв’язується методом послідовних наближень наступним чином.
Приймаємо b і a рівними нулю, тобто
Bm B1 ,
Am A1 ,
і з цими значеннями обчислюємо в першому наближенні bІ ,lІ ,aІ, а потім знаходимо
B |
|
B |
|
b I |
|
||
m |
|
|
, |
|
|||
|
|
||||||
|
1 |
2 |
|
|
|
||
|
|
|
|
|
(4.63) |
||
|
|
|
|
a I |
|||
A |
A |
|
|
||||
|
|
. |
|
||||
|
|
||||||
|
m |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
||
З цими наближеними значеннями знаходимо нові, більш точні значення Bm і Am та повторюємо обчислення b і a, а також l. Так поступають до тих пір, поки результати обчислень із двох суміжних наближень не стануть однаковими.

|
Тема 4. Розв'язування геодезичних задач |
|
|
|
|
|
|
|
|
||||||||||||
Обернена геодезична задача. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При відомих значеннях B1 , L1 , B2 , L2 |
ми можемо зразу знайти |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
B B |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bm |
1 |
, |
b B |
2 |
|
B , |
|
l L |
2 |
L . |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для знаходження невідомих s, A1 , A2 |
використовують отримані вище формули для прямої геодезичної |
||||||||||||||||||||
задачі. |
При цьому для обчислення |
|
A , A |
достатньо |
знайти |
A |
|
|
1 |
(A A |
180o ) |
та |
|||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
m |
|
|
2 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a A |
180o A . Тоді отримаємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A A |
|
1 |
a |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
m |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
A |
A |
|
a 180o |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
m |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Для знаходження Am представимо формули (4.60) та (4.61) у виді
s cos A |
Q bM |
|
|
l |
2 |
sin |
2 |
Bm |
|
|
|
l |
2 |
|
|||
1 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
m |
|
|
m |
|
|
|
24 |
|
|
|
|
12 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
s sin A |
P lN |
|
cos B |
|
|
|
|
l |
2 |
sin |
2 |
Bm |
|
|
|||
|
|
|
|
|
|
|
|
||||||||||
m |
m |
1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
m |
|
|
|
|
|
|
24 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
. (4.64)
b2 24
Розділивши ці два рівняння, отримаємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tgA |
m |
|
P |
. |
|
|
|
|
|
|
|
|
|
(4.65) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Величину a знаходимо на основі формули (4.62) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
a l sin B |
|
|
l |
2 |
sin |
2 |
Bm |
|
b |
2 |
|
l |
2 |
|
|
|
1 |
|
|
|
|
|
|
. |
(4.66) |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
m |
|
|
|
24 |
|
12 |
12 |
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||
Довжину геодезичної лінії s легко знаходимо із рівнянь (4.64)
s Q cos A |
P sin A |
|
Q2 P2 . |
(4.67) |
m |
m |
|
|
|
4.6.2. Розв’язування прямої геодезичної задачі методом допоміжної точки (формули Шрейбера)
Нехай на рис.4.8 PQ1Q2 – сфероїдний полярний трикутник, який потрібно розвязати за такими даними:
широтою B1 і довготою L1, довжиною s геодезичної лінії, що з'єднує точки Q1 i Q2, а також азимутом A1 цієї лінії в точці Q1 (прямий азимут).
Розділимо трикутник PQ1Q2 (див. рис.4.8.а) на два сфероїдних прямокутних трикутника геодезичною
лінією Q2С, яка перпендикулярна меридіану PQ1 початкової точки. Широту точки С позначимо через
Bo B1 b , а різницю широт Bo B2 - через d.
Вивід формул Шрейбера буде складатись із наступних етапів.
Із прямокутного сфероїдного трикутника Q1С Q2 за даними A1 і s визначають катети x і y,
використовуючи теорему Лежандра та сферичний надлишок цього трикутника. На рис. 4.8.б представлений трикутник Q1’Q2’C’, який відповідає сфероїдному трикутнику Q1 С Q2.
Застосовуючи формули розкладу в ряд (4.32) можна розв’язати пряму геодезичну задачу для точок Q1 і С.
Поскільки для цієї пари точок A1=0 і s=x, то все зводиться тільки до визначення різниці широт b.

Тема 4. Розв'язування геодезичних задач
За тими ж формулами розв’язують пряму геодезичну задачу з точки С , широта якої Bo B1 b тепер
вже відома, на точку Q2 , тобто при азимуті A1=90o та відстані s=y.
а) |
|
б) |
|
P |
C |
y |
2 |
l |
|
|
|
C(B0=B1+b) 900
(d)
b(x)
A1
 1(B1)
1(B1)
x |
s |
 1
1
y 900-a


















 2(B2=B0-d) A2
2(B2=B0-d) A2
s
Рис.4.7. Геометрична схема розв’язування головної геодезичної задачі методом Шрейбера.
Отже, замість прямого застосування рядів (4.32) до точок Q1 і Q2 їх застосовують послідовно до точок Q1
і С , а потім до точок С і Q2, тобто у випадках, коли A=0o і A=90o.
В результаті отримаємо: |
B2 B1 |
|
b d та |
L2 |
L1 |
l . |
|
|
|
|||||||||||||||||||||||||||||||||
Сума всіх кутів навколо точки Q2 дасть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
A2 |
|
90 o |
|
A1 |
90 o |
a 360 o , |
|
|||||||||||||||||||||||||
звідки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 A1 |
180 a . |
|
|
|
|
|
|
|
|
(4.68) |
|||||||||||||||||||
Розглянемо детальніше вивід основних формул. Із плоского трикутника Q1’С’Q2’, використовуючи |
||||||||||||||||||||||||||||||||||||||||||
теорему Лежандра, за формулою синусів отримаємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
cos(A |
|
2 |
) |
|
|
|
|
|
|
|
|
|
sin(A |
|
) |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
x s |
|
|
1 |
|
3 |
|
|
|
|
; |
|
|
|
|
|
|
|
y s |
|
|
|
|
|
|
1 |
|
3 |
|
|
|
, |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
(4.69) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
де сферичний надлишок може бути достатньо точно обчислений за формулою |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
P |
|
|
1 |
xy cos |
|
1 |
|
|
|
|
xy |
|
|
|
s 2 |
cos A sin A |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
. |
(4.70) |
|||||||||||||||
R2 |
|
2 |
3 MN |
|
2MN |
|
|
|
|
|
2MN |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Для визначення широти Bo, використаємо першу формулу системи (4.32), в якій при підстановці |
||||||||||||||||||||||||||||||||||||||||||
похідних (до третього порядку) врахуємо, що A 0o , s x : |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
B b B |
|
|
x |
|
|
|
3 |
|
x2 |
|
|
2tgB |
1 |
|
|
x3 |
|
|
2 |
(1 tg2 B ) . |
(4.71) |
||||||||||||||||||||
M |
|
|
2 M |
N |
|
2 M |
N |
|
|
|||||||||||||||||||||||||||||||||
o |
1 |
|
|
1 |
|
1 |
|
|
|
1 |
1 |
|
|
|
2 1 |
1 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
||

Тема 4. Розв'язування геодезичних задач |
|
|
|
||||||||||||||||||||
Аналогічно поступають і при визначенні широти B2, тільки в цьому випадку вже |
A 90o , s y : |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
1 |
|
|
y 2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
B2 Bo |
|
|
|
|
|
tgBo . |
|
|
|
|
|
(4.72) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 M o No |
|
|
|
|
|
|
||||||
Застосуємо тепер другу і третю формули системи (4.32) для визначення приростів довготи l та азимута a |
|||||||||||||||||||||||
відповідно. При цьому враховуємо, що |
A 90o , s y : |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
y |
|
1 |
|
|
y3 |
|
|
tg 2 Bo , |
|
|
|
|
||||||||
No cos Bo |
3 No |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
3 cos Bo |
|
|
|
|
|
(4.73) |
||||||||||||||
|
|
y |
|
|
1 y 3 |
|
|
|
|
|
|
|
|
|
|||||||||
a |
tgBo |
tgBo (1 2tg |
2 |
Bo |
o |
2 |
). |
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
No |
6 No 3 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Відповідно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
L2 |
L1 l, |
|
|
|
|
|
|
|
|
(4.74) |
||||||||||
|
|
|
A |
A 180o |
a . |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4.6.3. Розв’язування головних геодезичних задач методом переходу на поверхню сфери (формули
Бесселя)
Воснові способа Бесселя лежать умови:
1)геодезична лінія s між точками Q1 і Q2 еліпсоїда (рис.4.9.а) зображується на сфері дугою
великого кола між точками Q1' і Q2' (рис.4.9.б);
2)у відповідних точках геодезичної лінії і дуги великого кола азимути рівні;
Еліпсоїд |
P |
|
|
|
Сфера |
||||
|
l |
|
|
|
|
dl |
0 |
u |
|
|
|
|
- |
2 |
|
9 |
0 |
|
|
|
|
|
||
|
|
|
|
|
P
|
|
|
|
|
|
|
|
|
|
u |
1 |
|
|
|
|
|
|
|
0 |
9 |
0 |
- |
|
|
|
|
|||
|
|
|
|
||
|
|
|
|
|
ds
A1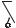 m
m
1(B1 ,L2)

n
s
A2

 A1 2(B2 ,L2)
A1 2(B2 ,L2) 
 1
1
|
|
A2 |
|
|
|
|
d |
|
m |
n |
2 |
|
|
|
а) |
б) |
Рис.4.9. Геометрична схема розв’язування головної геодезичної задачі методом Бесселя.
3)широта будь-якої точки на сфері рівна приведеній широті відповідної точки на еліпсоїді,
тобто сторони сферичного трикутника Q1' P' і Q2' P' відповідно рівні доповненням до 900 приведених
широт точок Q1 і Q2 на еліпсоїді.
Цими умовами забезпечується вище поставлена вимога однозначної відповідності між геодезичною
лінією на еліпсоїді і дугою великого кола на сфері. Така відповідність називається ще бесселевим зображенням.
Залишається встановити зв’язки між різницею довгот точок на еліпсоїді і аналогічною
величиною - на сфері; довжиною геодезичної лінії s на еліпсоїді і дугою великого кола на сфері. Хід отримання математичних формул цих зв’язків:
1.Вивід диференційних рівнянь, що встановлюють зв’язки між l і , s і .
