1 курс / 1 курс 2 семестр / Теория_вероятностей_9_22_лекц_1К

Теория вероятностей и математическая статистика

Проверим, выполняется ли требование конечности математических ожиданий:

M(Xn) = -n (1/2n2) + 0(1 – 1/n2) + n (1/2n2) = 0.

Таким образом, каждая конечная величина имеет конечное (равное нулю) математическое ожидание, то есть второе требование теоремы Чебышёва

выполняется.

61

Теория вероятностей и математическая статистика

Проверим, выполняется ли требование равномерной

Или, сложив вероятности одинаковых возможных значений,

62

Теория вероятностей и математическая статистика

Найдем математическое ожидание (2):

(2) = n2 2 1/n2 = 2.

Найдем дисперсию D(Xn):

Таким образом, дисперии данных случайных величин равномерно ограничены числом 2 , то есть третье

требование теоремы Чебышёва выполняется.

63

Теория вероятностей и математическая статистика

Итак, поскольку все требования выполняются, к

рассмотренной последовательности случайных величин теорема Чебышёва применима.

64

Теория вероятностей и математическая статистика

8.3. Теорема Бернулли

Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р.

Можно ли предвидеть, какова примерно будет относительная частота появлений события?

Положительный ответ на этот вопрос дает теорема,

доказанная Якобом Бернулли, получившая название «закона больших чисел» и положившая начало теории вероятностей как науке.

65

Теория вероятностей и математическая статистика

Теорема Бернулли, получившая название «закона больших чисел», впервые опубликована в 1713 г.

Доказательство Бернулли было сложным.

Простое доказательство этой теоремы дано Пафнутием Львовичем Чебышёвым в 1846 г.

66

Теория вероятностей и математическая статистика

Теорема Бернулли. Если в каждом из n независимых

испытаний вероятность р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.

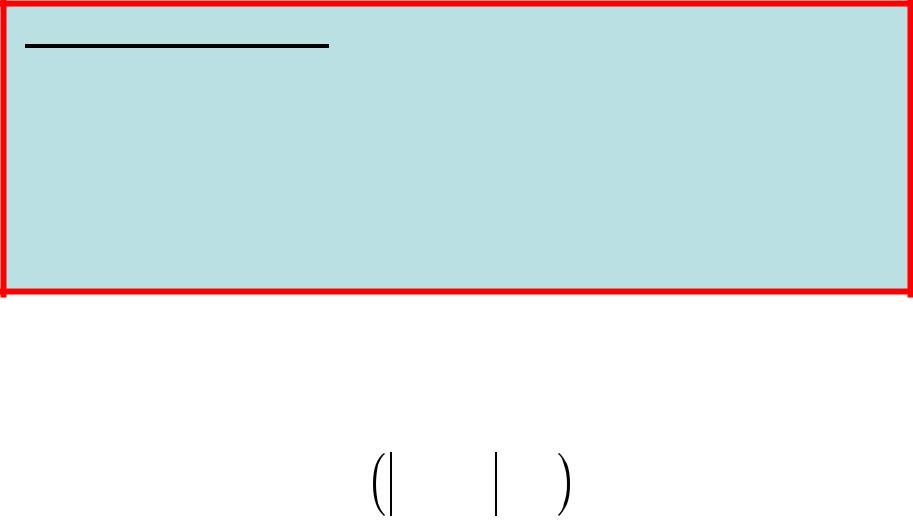
Другими словами, если — сколь угодно малое положительное число, то при соблюдении условий теоремы имеет место равенство

67

Теория вероятностей и математическая статистика

Таким образом, сходимость относительной частоты m/n к вероятности р отличается от сходимости в смысле обычного анализа. Для того чтобы подчеркнуть это различие, вводят понятие «сходимости по

вероятности»*.

*Последовательность случайных величин Х1, Х2, ...

сходится по вероятности к случайной величине X, если для любого > 0 вероятность неравенства | Хn — X | < при n ∞ стремится к единице.

68

Теория вероятностей и математическая статистика

Замечание. Было бы неправильным на основании теоремы Бернулли сделать вывод, что с ростом числа испытаний относительная частота неуклонно стремится к вероятности р; другими словами, из теоремы Бернулли

не вытекает равенство

В теореме речь идет лишь о вероятности того, что

при достаточно большом числе испытаний относительная частота будет как угодно мало отличаться от постоянной вероятности появления события в каждом испытании.

69

Теория вероятностей и математическая статистика

Точнее, различие между указанными видами сходимости состоит в следующем:

если m/n стремится при n ∞ к р как пределу в смысле обычного анализа, то начиная с некоторого n =

N и для всех последующих значений n неуклонно выполняется неравенство |m/n — р | < ;

если же m/n стремится по вероятности к р при n ∞,

то для отдельных значений n неравенство может

не выполняться.

70