
Лекции ХТП / Тема-2
.pdf
1 Тема 02
Тема 02. Построение: строение эмпирическихэмпирическихстат стических моделейстатистическихХТП моделей ХТП
§1. Основные понятия теории вероятностей и математической статистики
Вероятность события
p |
i |
P( X x |
) m / n |
|
i |
|
Суммарная вероятность
0 P 1
n |
|
pi |
1 |
i 1 |
|
распределена некоторым образом между отдельными значениями xi
x1 x2 x3 ... xn p1 p2 p3 ... pn
РХТУ им. Д.И. Менделеева |
Кафедра информатики и компьютерного моделирования |

2 Тема 02: Построение эмпирических статистических моделей ХТП
Соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностям, называется законом распределения вероятностей случайной величины.
Функция распределения непрерывной случайной величины
F(x) P( X x) P( X x)
Нормальное распределение
F (x) |
|
1 |
|
x e( x mX )2 /( 2σ2X ) dx |
|
|
|
||
2 |
||||
|
|
2πσ X |
|
|
РХТУ им. Д.И. Менделеева |
Кафедра информатики и компьютерного моделирования |
3 Тема 02: Построение эмпирических статистических моделей ХТП
Для дискретных случайных величин, так же как и для непрерывных, вводится
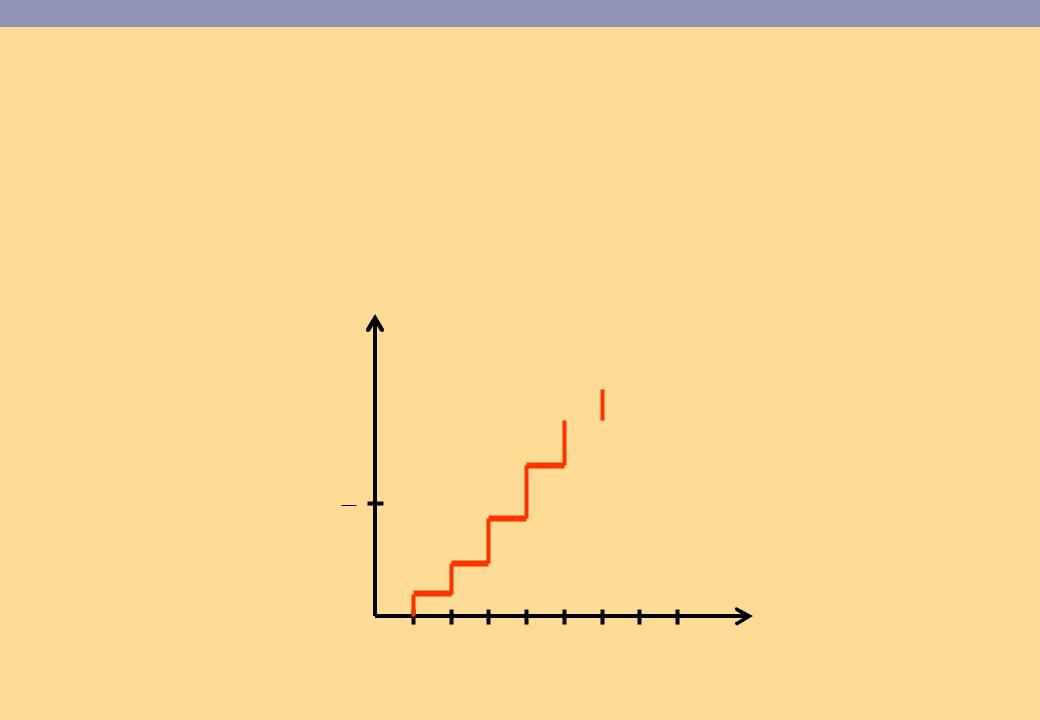
функция распределения дискретной случайной величины
|
|
|
n |
|
i |
|
n |
|
|
F (x) P( X x) |
|
|
|
|
|||||
|
|
p(x ), |
x |
|
x |
||||
|
|
|
i 1 |
|
|
|
|
|
|
|
|
F x |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2
x
РХТУ им. Д.И. Менделеева |
Кафедра информатики и компьютерного моделирования |
4 Тема 02: Построение эмпирических статистических моделей ХТП
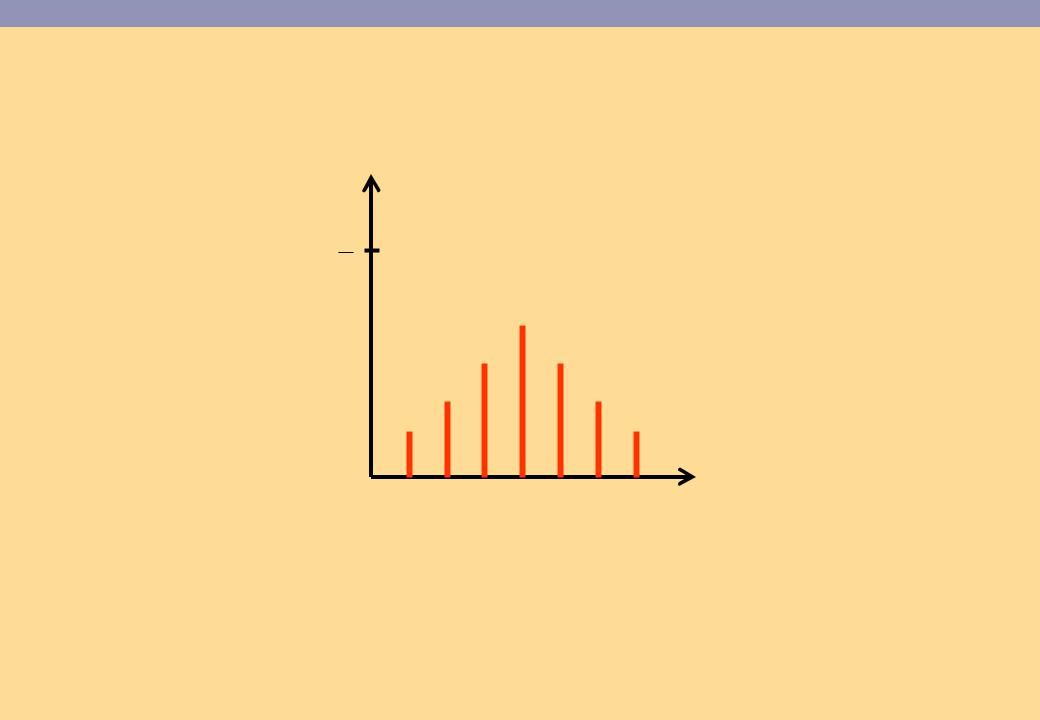
Вместо функции плотности распределения иногда используется распределение вероятностей дискретной случайной величины
p x
1 2
x
РХТУ им. Д.И. Менделеева |
Кафедра информатики и компьютерного моделирования |

5 Тема 02: Построение эмпирических статистических моделей ХТП
Случайные величины определяют с помощью числовых характеристик, выражающих особенности случайных величин
Математическое ожидание - характеризует центр рассеяния случайной
величины
m |
X |
|
|
n |
|
|
|
i |
i |
|||
|
|
x p |
||
i 1 |
|
|||
M[ X ] |
|
|
|
|
|
|
|
||
|
xf (x) |
|||
|
||||
|
|
|||
|
|
|
||
- если Х дискретна
dx |
- если Х непрерывна |
|
РХТУ им. Д.И. Менделеева |
Кафедра информатики и компьютерного моделирования |

6 Тема 02: Построение эмпирических статистических моделей ХТП
Дисперсия - характеризует разброс значений случайной величины относительно ее центра (математического ожидания)
σ |
2 |
M [( X m |
|
2 |
] |
X |
X |
) |
|||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( X i |
mX |
||||
|
|
|
|
|
|
|
|
σ |
2 |
i 1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
) |
2 |
|
|
|
|
|
|
|
||
|
|
|
(x m |
X |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
2 |
p |
- если Х дискретна |
|
|||
|
|
i |
|
|
|
|
f (x)dx |
- если Х непрерывна |
РХТУ им. Д.И. Менделеева |
Кафедра информатики и компьютерного моделирования |

7 Тема 02: Построение эмпирических статистических моделей ХТП
Выборочный метод
По выборке могут быть рассчитаны выборочные статистические характеристики, которые являются оценками соответствующих генеральных параметров.
Оценки математического ожидания (выборочного среднего):
|
n |
|
ˆ |
* |
|
mX |
x xi |
pi |
|
i 1 |
|
Оценки дисперсии:
n
σˆ 2X DX (xi* x)2 pi i 1
РХТУ им. Д.И. Менделеева |
Кафедра информатики и компьютерного моделирования |

8 Тема 02: Построение эмпирических статистических моделей ХТП
Пример. Дана выборка объема n = 50 со следующей таблицей распределения:
x |
i |
|
|
n |
i |
|
1 |
2 |
3 |
4 |
20 |
15 |
10 |
5 |
|
|
|
|
Найти выборочное среднее и выборочную дисперсию.
Решение.
Учитывая, что |
p |
|
n /n |
|
i |
||||
|
|
i |
получаем формулу для расчета выборочного среднего:
|
n |
|
x |
ni xi |
|
i 1 |
||
|
||
|
n |
x |
20 1 15 2 10 3 5 4 |
2 |
|||
20 |
|
15 10 5 |
|||
|
|
||||
Вычисляем оценку выборочной дисперсии :
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ni (xi |
x)2 |
|
|
20(1 2) |
2 |
15(2 |
2) |
2 |
10(3 |
2) |
2 |
5(4 |
2) |
2 |
|
|
D |
|
|
i 1 |
|
D |
|
|
|
|
|
|
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
X |
n |
|
X |
|
|
|
|
50 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
РХТУ им. Д.И. Менделеева |
Кафедра информатики и компьютерного моделирования |

9 Тема 02: Построение эмпирических статистических моделей ХТП
Оценки параметров распределения случайной величины
Понятие интервальной оценки связано с понятием доверительной вероятности и доверительного интервала.
Доверительной вероятностью |
β |
значение оцениваемого параметра
называется вероятность того, что истинное
θ |
заключено в интервале |
ˆ |
|
ˆ |
|
) |
β P(θ ε |
β |
θ θ ε |
β |
|
|
|
|
Границы этого интервала
ˆ |
|
θ ε |
β |
|
и
ˆ |
|
θ ε |
β |
|
называются
доверительными границами, а сам интервал – доверительным интервалом.
Для определения границ доверительного интервала необходимо найти точечную
оценку параметра |
θ |
и точность этой оценки εβ , т.е. разброс оценки |
ˆ |
θ |
вокруг истинного значения параметра θ .
РХТУ им. Д.И. Менделеева |
Кафедра информатики и компьютерного моделирования |

10 Тема 02: Построение эмпирических статистических моделей ХТП
Распределение Стьюдента (малые объемы выборок)
Закон распределения Стьюдента используется, когда значения оценок x и определяются по выборкам, объем которых n < 50.
Случайная величина t – распределения Стьюдента определяется:
σ |
X |
|
t |
x m |
X |
n |
|
|
|
|||
|
|
|
|
|
|
S |
X |
|
|
|
|
|
|
|
|
X |
|
n |
i |
|
|
|
S |
|
|
2 |
|
|
||
|
|
|
(x x) |
|
(n 1) |
||
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
Число степеней свободы выборки объемом n обозначается
ν n 1
ν
и определяется как
Выражение, определяющее доверительный интервал для малых выборок:
n |
|
|
|
|
|
|
|
n |
|
|
|
|
xi |
t ν |
S |
|
|
|
|
|
xi |
t ν |
S X |
|
|
i 1 |
X |
|
m |
|
|
i 1 |
|
|||||
|
|
|
|
X |
|
|
|
|
||||
|
|
|
|
|
||||||||
n |
1 p / 2 |
|
n |
|
n |
1 p / 2 |
|
n |
|
|||
|
|
|
|
|
|
|
||||||
РХТУ им. Д.И. Менделеева |
Кафедра информатики и компьютерного моделирования |
