Учебники 80358

Таблица 2.14

Матричный вид функции полезности

Вариант состояния среды

Вариант решения

Таблица 2.15

Матричный вид функции потерь

Вариант состояния среды

Вариант решения

Особенностью рассматриваемой задачи является ее однокритериальность. Здесь основное внимание будет сосредоточено на преодолении неопределенности в значениях одного локального критерия качества, представленного функцией полезности или потерь.

Отметим, что альтернативе соответствует несколько значений полезности , или потерь локального критерия или характеристики качества при разных . Иными словами, выбор

альтернативы не приводит к однозначному результату.

Задача принятия решений состоит в выборе ЛПР наилучшего варианта (или строки матрицы при представлении функции полезности или потерь в виде

221

в зависимости от смысла оценки

локального критерия качества .

Критерий оценки и выбора решений можно рассматривать как операцию предпочтения на множестве альтернатив с учетом элемента неопределенности возможных состояний среды упорядочивающую

совокупность решений в транзитивную последовательность в порядке предпочтительности. С помощью критерия оценки значений локального критерия (характеристики) качества преодолевается неопределенность состояний среды и выбирается лучшее в смысле применяемого критерия оценки решение. Поэтому логично называть данные критерии также критериями снятия неопределенности

Формальную схему определения критерия оценки и выбора решений в условиях неопределенности представим в виде обобщенного алгоритма.

Алгоритм

1.Сформировать множество решений .

2.Сформировать множество состояний среды .

3.ЛПР определить значения оцениваемого локального

.

4.ЛПР оценить ситуацию априорной информированности, характеризующую поведение среды.

5.ЛПР выбрать или сконструировать критерий снятия неопределенности, соответствующий ситуации априорной информированности.

6.Используя полученную модель, решить задачу выбора

ипроанализировать решение. В случае необходимости

222

провести корректирование полученной модели и заново решить задачу.

Далее рассмотрены основные критерии оценки и выбора решений (критерии снятия неопределенности) для каждой из трех ситуаций априорной информированности.

2.5.2. Построение критериев оценки и выбора решений для первой ситуации априорной информированности ЛПР

Рассмотрим основные критерии оценки и выбора решений (снятия неопределенности) в первой ситуации априорной информированности ЛПР, характеризующейся

2.5.2.1. Критерий Байеса-Лапласа

Согласно критерию Байеса-Лапласа каждое решение описывается следующим критерием:

-для функции полезности

-для функции потерь

где в записи критерия первый нижний индекс означает номер критерия оценки и выбора решений (снятия неопределенности); вектор введен для того, чтобы отразить

байесовым значением функции полезности для решения . Если используется функция потерь, то величину называют байесовым риском для

решения, для которых математическое ожидание функции полезности или функции потерь достигает экстремального значения:

-для функции полезности

-для функции потерь

Смысл критерия заключается в максимизации математического ожидания функции полезности и преобразовании априорных вероятностей в апостериорные.

Правило выбора по критерию Байеса-Лапласа для дискретного множества решений можно интерпретировать следующим образом.

Матрица решений , дополняется еще одним столбцом, содержащим математическое ожидание значений каждой из строк . Выбираются те варианты , в строках которых стоит наибольшее значение 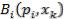этого столбца.

Для функции потерь 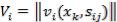матрица дополняется еще одним столбцом, содержащим математическое ожидание значений каждой из строк 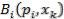. Выбираются те варианты 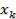, в строках которых стоит наименьшее значение этого столбца.

224

Критерий Байеса-Лапласа учитывает только усредненные значения функции полезности или потерь и не учитывает диапазона изменения значений функции полезности или потерь, рассеяния ее значений, что иногда приводит к неудовлетворительным решениям.

2.5.2.2. Критерий минимума среднего квадратического отклонения функции полезности или функции потерь

Среднее квадратическое отклонение 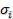характеризует рассеяние случайной величины функции полезности (потерь) для решения х относительно среднего значения и, например, в задачах финансовой математики часто трактуется как величина риска.

Смысл критерия минимизации среднего квадратического отклонения функции полезности (потерь) заключается в нахождении решения х*, для которого

225

Основным недостатком этого критерия является то, что среднее квадратическое отклонение решения 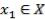может оказаться меньше, чем для решения , в то время как , т.е. выбирается самое определенное решение с пренебрежением величиной его полезности. Это говорит о том, что критерий минимума среднего квадратического отклонения функции полезности часто нельзя применять без наложения дополнительных требований.

Среднее квадратическое отклонение функции полезности или потерь можно вычислять по модифицированным формулам, учитывающим максимальные или минимальные, а также средние байесовские значения:

для

для

226

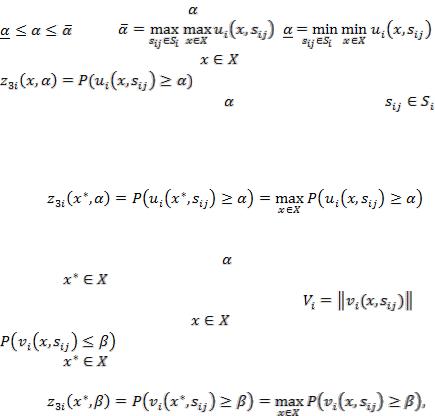
2.5.2.3. Критерий максимизации вероятности распределения функции полезности

Смысл критерия максимизации вероятности распределения функции полезности заключается в нахождении решения 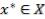, для которого

При использовании этого критерия ЛПР исходит из

где значение 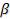выбирается ЛПР из отрезка .

2.5.2.4. Модальный критерий

Модальный критерий конструируется исходя из наиболее вероятного состояния среды.

Предположим, что существует единственное значение 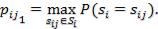В этом случае ЛПР полагает, что среда

227

определяется из условия

Основным недостатком рассматриваемого критерия является возможность того, что если взять два решения и

.

К преимуществам модального критерия можно отнести: использование наиболее вероятных состояний среды; при этом совсем не обязательно знать количественные значения самих вероятностей

осуществления этих состояний; возможность определения функции полезности

лишь для наиболее вероятных состояний среды, что во много раз увеличивает скорость принятия решения.

Отметим, что при использовании функции потерь операция max заменяется на min.

228

2.5.2.5. Критерий минимума энтропии математического ожидания функции полезности

Прежде чем описывать критерий, дадим краткое описание энтропии. Энтропия может служить мерой оценки

неопределенности.

математического ожидания функции полезности для решения 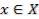определим следующим образом:

Здесь в качестве вероятностей выступают взвешенные нормализованные величины

Требуется найти решение (либо X*) из условия

229

Вслучае невыполнения условия для всех

и выполняется переход от значений функции полезности к риску (сожалениям, потерям)

вида

В этом случае решение находится из условия минимума по энтропии математического ожидания функции полезности вида при :

2.5.2.6. Критерий Гермейера

Рассмотрим критерий Гермейера, ориентированный на

Во многих прикладных задачах приходится иметь дело с

положительные значения, можно перейти к строго