
Учебники 80358
.pdf
бинарных отношений, на основе которых последовательно исключаются из рассмотрения худшие альтернативы. Процедура выбора заканчивается, когда остается приемлемое для ЛПР число лучших альтернатив.
2.4.1. Постановка многокритериальных задач принятия решений
Формальное описание модели многокритериальной задачи принятия решений при определенности представлено в разделе 2.2. Поставленная задача является при этом не совсем некорректной, поскольку она имеет решение только в том редком случае, когда максимум всех m критериев достигается в одной точке. Обычно критерии являются противоречивыми, и улучшение (увеличение) значений по одному из критериев приводит к ухудшению (уменьшению) значений по другим критериям. В этой ситуации необходимо искать компромисс.
Следует отметить, что далее рассматривается задача максимизации. Такой выбор связан с функцией качества решения, характеризующей величину изменения риска, значение которой, естественно, желательно увеличить.
При наличии различного характера локальных критериев необходимы предварительное преобразование и нормализация этих критериев. Если в качестве критериев выбраны затраты, потери и др., которые надо минимизировать, то задача минимизации преобразуется в задачу максимизации изменением знака локальных критериев: – 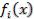 .
.
Для преодоления неопределенности, связанной с многокритериальностью, необходимо:
ввести понятия лучших решений; использовать принципы оптимальности, которые
обеспечивают способы сравнения решений в пространстве критериев; разработать методы для поиска компромиссных решений.
161

Принятие решений заключается в выборе ЛПР альтернатив (действии) для перевода объекта из текущего состояния в желаемое. Реализация той или иной альтернативы обычно приводит к различным исходам, состояниям объекта. Для сравнения между собой качеств разных альтернатив необходимо иметь возможность оценивать соответствующие исходы (результаты) выбора. Исход операции выбора может оцениваться с помощью некоторых обобщенных критериев качества (критериев оптимальности), которые являются математическим выражением цели принятия решений, позволяющим оценить степень достижения этой цели.
Процедура принятия решений включает следующие общие операции [68]:
описание ситуации и оценка ресурсов; формирование множества критериев, ограничений, альтернатив; оценивание критериев и альтернатив;
формирование правил выбора; упорядочение альтернатив по многомерным признакам; выбор и принятие решений.
Методы выполнения перечисленных действий образуют основы теории принятия решений. Они позволяют ЛПР успешно решать многие сложные задачи эффективного выбора, систематизируя и формализуя его действия при принятии решений.
2.4.2. Характеристики приоритета критериев. Нормализация критериев
Задачи принятия решений в условиях определенности
характеризуются однозначной |
детерминированной |
связью |
между альтернативами |
и результатом |
выбора |
. Разные критерии могут иметь |
||
различную важность с точки |
зрения ЛПР. Рассмотрим |
|
162 |
|
|

некоторые способы описания относительной важности критериев [68].
Ряд приоритета. Ряд приоритета 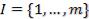 отражает упорядочение критериев по важности (ранжировку:
отражает упорядочение критериев по важности (ранжировку:
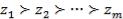 и выражает существование более важных, менее важных и равноважных (эквивалентных по важности)
и выражает существование более важных, менее важных и равноважных (эквивалентных по важности)
критериев. |
|
Например, |
. Приведенная запись |
означает, что критерии упорядочены по важности и самый важный критерий имеет номер 1(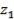 ); следующий по важности критерий — номер 2(
); следующий по важности критерий — номер 2(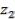 ); критерии с номерами 3 и 4(
); критерии с номерами 3 и 4(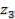 и
и  ) имеют одинаковую важность и наименее важный критерий имеет номер m(
) имеют одинаковую важность и наименее важный критерий имеет номер m( ). В данной записи критерии пронумерованы в порядке уменьшения важности.
). В данной записи критерии пронумерованы в порядке уменьшения важности.
Вектор приоритета. В векторе приоритета
|
показывает |
для упорядоченных |
по |
|
важности критериев, во сколько раз критерий |
, более важен, |
|||
чем критерий |
. Алгоритм |
получения |
состоит |
в |
следующем: |
последовательно |
при |
|
|
рассматривают приращения критериев, берут единичное
приращение критерия |
и находят такое приращение критерия |
, которое равно |
единичному изменению качества по |
критерию . Полученная величина обозначается . |
|
Весовой вектор. В весовом векторе |
– |
представляет относительную важность i-го критерия |
по |
отношению ко всем остальным критериям. Из данного определения следует связь между элементами весового вектора 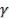 и вектора приоритета
и вектора приоритета  :
:
 ,
,
В данном случае рассматривается нормализованный весовой вектор 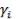
 , для которого выполняются следующие условия:
, для которого выполняются следующие условия:
163
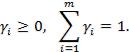
Если у весового вектора все значения 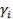 равны, то задача называется задачей без приоритета.
равны, то задача называется задачей без приоритета.
Нормализация критериев. Часто критерии измеряются в разных единицах, шкалах; для одних критериев лучшие значения – это те, которые больше, а для других, наоборот, меньше. Чтобы сравнивать значения разных критериев, необходимо перейти к однонаправленным шкалам, выразить их значения в одинаковых абсолютных единицах либо перейти к безразмерным шкалам. Для таких преобразований значений критериев используют следующие операции, называемые нормализацией критериев.
1.Смена направленности цели (замена max на min
или min на max): 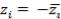 , где
, где  ,
,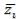 – нормализованная и исходная величины критерия. Предполагается, что критерии описывают достижение некоторой цели. Данный способ применяют для перехода к однонаправленным критериям.
– нормализованная и исходная величины критерия. Предполагается, что критерии описывают достижение некоторой цели. Данный способ применяют для перехода к однонаправленным критериям.
2.Нормализация по заданному значению:
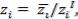 где
где 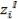 – заданная или идеальная величина критерия. Здесь осуществляется переход к безразмерной шкале. Обычно предполагается, что все исходные значения критериев либо неотрицательны, либо неположительны. В последнем случае происходит смена направлений цели.
– заданная или идеальная величина критерия. Здесь осуществляется переход к безразмерной шкале. Обычно предполагается, что все исходные значения критериев либо неотрицательны, либо неположительны. В последнем случае происходит смена направлений цели.
3.Относительная нормализация: 
Представляет собой частый случай нормализации по заданному значению.
4.Сравнительная нормализация: 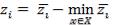
Данная нормализация совмещает наименьшее значение критерия с нулем, и все значения критериев становятся неотрицательными.
164

5. |
Естественная |
нормализация: |
Обычно предполагается, что исходные значения критериев неотрицательны. Если это не так, то с помощью сравнительной нормализации переходят к неотрицательным значениям критериев.
6. Нормализация Севиджа:
Данная нормализация совмещает наибольшее значение критерия с нулем, все значения критериев становятся неотрицательными и происходит изменение направленности критерия, т. е. лучшими значениями критерия становятся меньшие.
7. Полная
Данная нормализация является объединением сравнительной и естественной нормализации и отображает исходные значения критериев на отрезок от нуля до единицы. Лучшее значение нормализованного критерия равно единице, а худшее – нулю.
2.4.3. Принципы оптимальности в задачах принятия решений
Рассмотрим подход к проблеме многокритериальности, основанный на введении понятия лучших решений и опирающийся на постулируемые принципы оптимальности. Принципы оптимальности можно трактовать как обобщенные критерии качества (критерии оптимальности), являющиеся математическим выражением цели принятия решений, которое позволяет оценить степень достижения этой цели. Выбор принципа или его конструкции остается за ЛПР [68].
Принцип оптимальности по Парето. Данный принцип может быть использован на начальной стадии решения задачи в целях уменьшения исходного множества решений 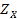 .
.
165
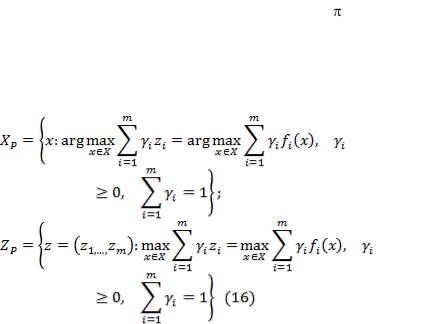
Решение (альтернативу) называют оптимальным по Парето (парето-оп- тимальным, паретовским, эффективным), если невозможно улучшить (увеличить) решение ни по одному из критериев без ухудшения (уменьшения) решения хотя бы по одному из критериев. Парето-оптимальные решения (альтернативы) составляют множество Парето (множество эффективных решений, множество -оптимальных альтернатив, множество компромиссов).
Пусть  является множеством Парето в пространстве независимых переменных (параметров) и
является множеством Парето в пространстве независимых переменных (параметров) и  — множество Парето в пространстве критериев. Тогда эти множества могут быть описаны следующими моделями:
— множество Парето в пространстве критериев. Тогда эти множества могут быть описаны следующими моделями:
Данное описание корректно для выпуклого множества  . На рис. 2.3 приведены примеры выпуклых паретовских множеств для непрерывного и дискретного случаев.
. На рис. 2.3 приведены примеры выпуклых паретовских множеств для непрерывного и дискретного случаев.
166
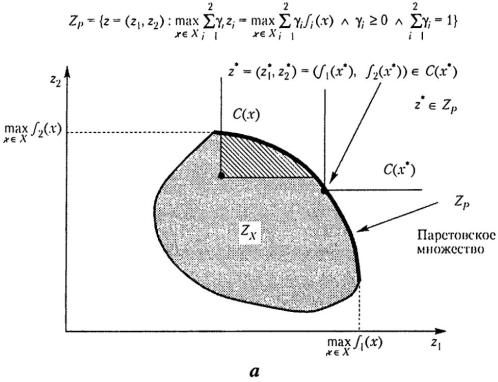
Рис. 2.3. Примеры выпуклых непрерывного (а) и дискретного (б) множеств Парето
167
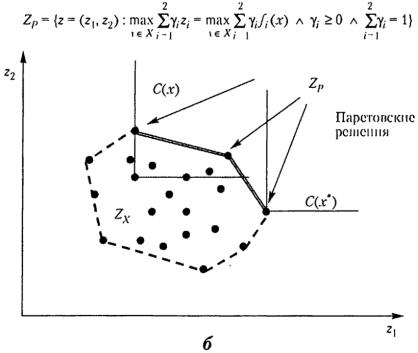
Рис. 2.3. Примеры выпуклых непрерывного (а) и дискретного (б) множеств Парето (продолжение)
168
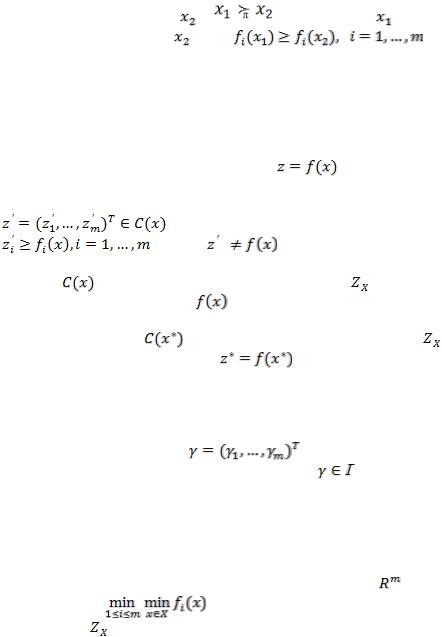
Введем еще одно понятие. Альтернатива 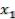 доминирует
доминирует
по Парето альтернативу |
( |
альтернатива |
лучше |
по Парето альтернативы |
), если |
|
, и |
хотя бы для одного i такое неравенство является строгим. Те альтернативы, для которых не существует доминирующих их допустимых альтернатив 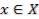 , называются оптимальными по Парето.
, называются оптимальными по Парето.
Множество альтернатив (векторных оценок) в пространстве критериев, доминирующих по Парето
альтернативу х |
(векторную |
оценку |
|
, |
совпадает с |
||
положительным |
ортантом |
(конусом) С(х), вершина которого |
|||||
перенесена в точку |
f(x). |
Для любой |
точки (альтернативы) |
||||
|
|
|
|
выполняются |
|
неравенства |
|
|
. |
Если |
, |
то |
хотя |
бы одно из |
|
неравенств будет строгим. Если пересечение положительного
ортанта |
с множеством векторных оценок |
содержит |
|
какие-либо |
точки кроме |
, то каждая из |
этих точек |
доминирует х по Парето. Альтернатива х* π-оптимальна, если
пересечение конуса |
с множеством векторных оценок |
|
состоит из единственной точки |
. |
|
Применение |
описанной |
методики позволяет легко |
проверять π-оптимальность альтернативы.
Структура моделей (15) приводит к простому алгоритму построения множества Парето: определить множество Г
величин весового вектора |
, |
найти паретовские |
точки по выражению (15) для |
каждого |
, построить |
конечно-разностную аппроксимацию пареговского множества по полученным точкам.
Рассмотрим более общий случай, когда множество 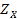 невыпукло. Предположим, что множество векторных оценок
невыпукло. Предположим, что множество векторных оценок 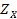 ограничено, замкнуто и целиком лежит во внутренности
ограничено, замкнуто и целиком лежит во внутренности
неотрицательного ортанга пространства критериев |
. Это |
|
означает, что |
. Ограниченность и замкнутость |
|
множества |
гарантирует существование π-оптимальных |
|
|
169 |
|
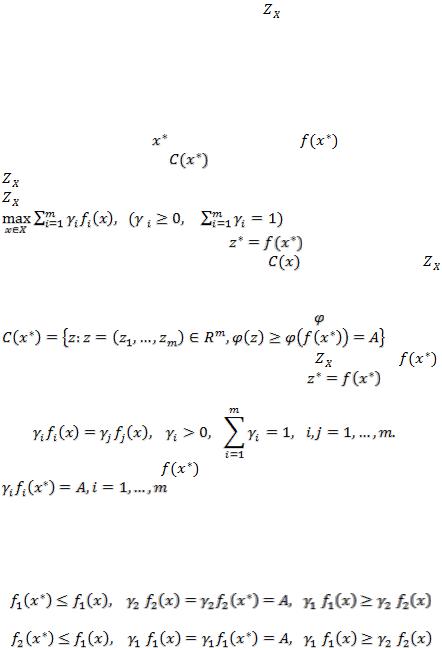
альтернатив. Условие того, что |
целиком лежит во |
||
внутренности |
неотрицательного |
ортанта |
пространства |
критериев, введено для удобства. Любое ограниченное множество в 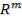 можно сдвинуть в положительный ортант, например, используя сравнительную нормализацию, и отношение доминирования по Парето между точками не изменится.
можно сдвинуть в положительный ортант, например, используя сравнительную нормализацию, и отношение доминирования по Парето между точками не изменится.
Пусть в точке |
векторная оценка |
π-оптимальна, |
||
т.е. пересечение конуса |
с множеством векторных оценок |
|||
состоит только из этой точки. При невыпуклом множестве |
||||
может |
не |
существовать |
функция |
вида |
|
|
, |
которая |
достигла |
максимального значения в точке |
. |
|
||
Так как |
пересечение конуса |
с множеством |
||
состоит из единственной точки, то можно считать, что граница этого конуса является множеством (поверхностью) уровня
некоторой |
функции |
, |
где |
|
|
, |
|
которая достигает максимума на множестве |
в точке |
. |
|
Проведем через начало координат и точку |
прямую |
||
линию, которая описывается уравнениями |
|
|
|
В |
точке |
выполняются |
условия |
.
В двумерном случае при 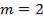 легко заметить, что линиями уровня функции
легко заметить, что линиями уровня функции 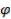 , проходящими через точку
, проходящими через точку 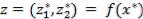 , являются лучи, идущие из точки
, являются лучи, идущие из точки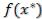 и удовлетворяющие условиям:
и удовлетворяющие условиям:
для луча под прямой
для луча над прямой
170
