Учебники 80358

На рис. 2.7 и 2.8 приведена графическая иллюстрация применения принципа равенства для случаев невыпуклых дискретного и непрерывных множеств .

Рис. 2.7. Примеры удачного применения принципа равенства для невыпуклых дискретного (а)

и непрерывного (б) множеств

181

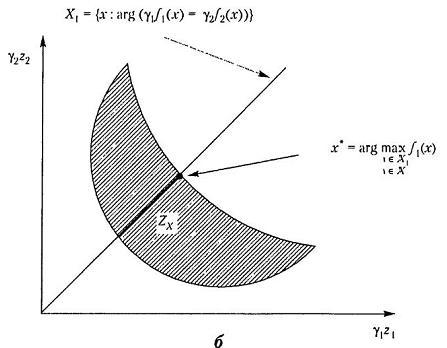
Рис. 2.7. Примеры удачного применения принципа равенства для невыпуклых дискретного (а)

и непрерывного (б) множеств (продолжение)

182

Рис. 2.8. Пример неудачного применения принципа равенства для невыпуклого непрерывного множества

Принцип квазиравенства. Это смягченная версия слишком «жесткого» принципа равенства. По данному принципу наилучшее решение определяется как точка:

заранее выбранная константа или величина, изменяемая ЛПР, которая позволяет значениям критериев отклоняться друг от друга.

На рис. 2.9 и 2.10 приведена графическая иллюстрация принципа квазиравенства для случаев невыпуклых дискретного и непрерывных множеств .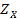

183

Рис. 2.9. Примеры применения принципа квазиравенства для невыпуклых дискретного (а) и непрерывного (б) множеств

184

Рис. 2.9. Примеры применения принципа квазиравенства для невыпуклых дискретного (а)

и непрерывного (б) множеств (продолжение)

185

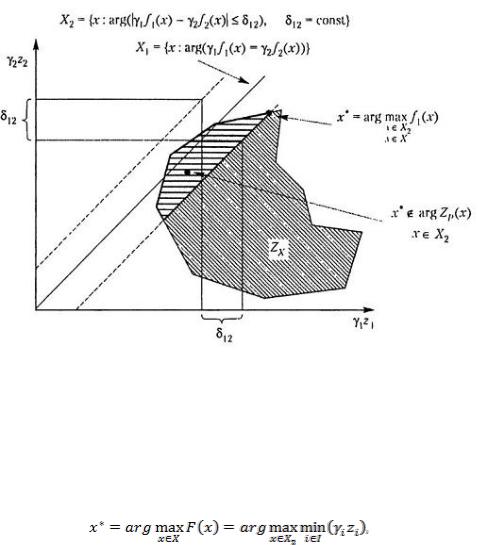
Рис. 2.10. Пример неудачного применения принципа квазиравенства для невыпуклого непрерывного множества

Принцип максимина. По данному принципу каждое решение описывается наименьшей взвешенной величиной из m критериев. Затем выбирается наибольшее среди этих наименьших значений и соответствующее ему решение принимается за наилучшее:

где — множество номеров критериев, ряд приоритета.

Иногда данный принцип называют принципом гарантированного результата или принципом наибольшей осторожности. Для графической иллюстрации можно

186

рассмотреть рис. 2.6. Максимннное решение в этих примерах совпадает с решением, полученным с помощью принципа равенства. На рис. 2.7 указано найденное максиминное решение при отсутствии решения по принципу равенства.

Принцип последовательного максимина. Если принцип максимина не приводит к единственному решению, то он может быть последовательно применен до m раз:

где 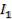– множество номеров критериев, полученное из множества I, из которого исключена единица (номер критерия с минимальным значением);

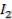— множество номеров критериев, полученное из множества , из которого исключена двойка; ...; — множество, которое содержит только число m (состоит из номера одного критерия).

Квазиоптимальный принцип последовательного максимина. Это смягченная версия принципа последовательного максимина. Принцип последовательного максимина может быть последовательно применен до m раз. Каждое максиминное i-e решение ослабляется на величину 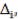такое ослабление производят до m раз. По данному принципу наилучшее решение ищется как точка:

где

– заранее выбранные константа или величины (изменяемые ЛПР), которые позволяют расширить множество допустимых значений. Критерий для максимизации может быть выбран ЛПР.

187

Стремление увеличивать значения всех критериев одновременно является привлекательным. Однако отклонение от приведенных принципов иногда может дать значительный выигрыш, например, если позволить ухудшать значения части критериев для достижения улучшения значений по другим критериям.

Следующие два принципа носят название принципов справедливой уступки. Понятие «справедливости» может быть описано разными способами. До сих пор не установлено простого и очевидного «справедливого» принципа. Он и не может существовать, поскольку различные ситуации требуют разной «справедливости». Компромисс и справедливость всегда привязаны к конкретной ситуации или к классу ситуаций. Рассмотрим подход к «справедливости», основанный на сравнении оценок увеличения и уменьшения значений локальных критериев при сравнении различных решений. Данный подход приводит к двум принципам: абсолютной и относительной уступки.

Принцип абсолютной уступки. Пусть сравниваются два любых решения и осуществляется переход от первого ко второму решению. Пусть при этом переходе величины одной части критериев уменьшаются, а второй — увеличиваются. Согласно рассматриваемому принципу второе решение лучше первого, если сумма взвешенных значений увеличившихся критериев больше суммы взвешенных значений уменьшившихся критериев. Это определение и принцип абсолютной уступки могут быть выражены в простой математической форме:

Описанный принцип позволяет улучшать качество решения за счет компенсации (уступки) уменьшения значений по одним критериям большим увеличением значений по другим критериям. Приведенная свертка в виде взвешенной

188

суммы величин критериев может рассматриваться как целевая функция или функция качества.

На рис. 2.11 и 2.12 дана графическая иллюстрация принципа абсолютной уступки для случаев невыпуклых и выпуклого дискретного и непрерывных множеств .

Рис. 2.11. Примеры применения принципа абсолютной уступки для невыпуклых дискретного (а)

и непрерывного (б) множеств

189

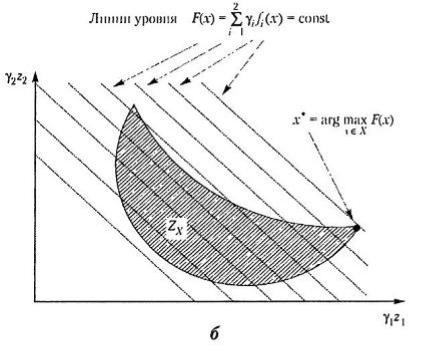
Рис. 2.11. Примеры применения принципа абсолютной уступки для невыпуклых дискретного (а) и непрерывного (б) множеств 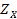(продолжение)

190