
Учебники 80358
.pdf
Метрика  при выполнении некоторых аксиом (неотрицательности, независимости от перестановок, перенумерации объектов, правила треугольника и др.) определяется по известной формуле:
при выполнении некоторых аксиом (неотрицательности, независимости от перестановок, перенумерации объектов, правила треугольника и др.) определяется по известной формуле:
Используя введенную метрику, можно определить обобщенную ранжировку как точку, которая наилучшим образом согласуется с точками, представляющими собой ранжировки экспертов. На практике наилучшее согласование чаще всего определяется как медиана или средняя ранжировка.
Медиана — точка в пространстве ранжировок, сумма расстояний от которой до всех точек — ранжировок экспертов является минимальной:
Средняя ранжировка определяется как точка, сумма квадратов расстояний от которой до всех точек — ранжировок экспертов является минимальной:
Если учитывается компетентность экспертов, то медиана и средняя ранжировка определяются из условий
где  — коэффициент компетентности z'-го эксперта.
— коэффициент компетентности z'-го эксперта.
Если ранжирование объектов проводится по нескольким показателям, то сначала определяется медиана по всем показателям для каждого эксперта, а затем — медиана по множеству экспертов.
Основным недостатком рассмотренного выше подхода определения обобщенной ранжировки является трудоемкость
141

расчетов. Естественный способ отыскания  или
или  перебором всех точек пространства ранжировок с увеличением количества объектов также становится неприемлемым, поскольку при этом очень быстро возрастает размерность пространства и, следовательно, объем вычислений.
перебором всех точек пространства ранжировок с увеличением количества объектов также становится неприемлемым, поскольку при этом очень быстро возрастает размерность пространства и, следовательно, объем вычислений.
Расхождение обобщенных ранжировок при различных критериях возникает при малом числе экспертов и несогласованности их оценок. Если мнения экспертов близки, то обобщенные ранжировки, построенные по критериям медианы и среднего значения, будут совпадать.
Сложность вычисления медианы или средней ранжировки привела к необходимости применения более простых методов построения обобщенной ранжировки.
1. Метод суммирования рангов заключается в ранжировании объектов по величинам сумм рангов  , полученных каждым объектом от всех экспертов. Для матрицы ранжировок
, полученных каждым объектом от всех экспертов. Для матрицы ранжировок  составляются суммы
составляются суммы
Далее объекты упорядочиваются в порядке возрастания суммы рангов.
2. Еще одним более обоснованным в теоретическом отношении подходом к построению обобщенной ранжировки является переход от матрицы ранжировок к матрице парных сравнений и вычисление собственного вектора, соответствующего максимальному собственному числу этой матрицы. Упорядочение объектов проводится по величине компонентов собственного вектора.
Рассмотрим вопросы оценки согласованности мнений экспертов. При обработке результатов ранжирования часто возникает задача определения зависимости между ранжировками двух и более экспертов, задача оценки связи между достижением различных целей при решении одной и
142

той же совокупности проблем или задача оценки взаимосвязи между разными признаками.
Решение данных задач проводится с помощью оценки ранговой корреляции. Под ранговой корреляцией понимается статистическая связь между ранжировками. Эта связь анализируется на основании исходных статистических данных,
представленных ранжировками |
экспертов |
альтернатив в |
виде матрицы |
, где |
– ранговая |
оценка  -го эксперта для -й альтернативы. Статистический анализ дает ответ на вопрос о том, есть ли какая-то согласованность (или связь) между упорядочениями анализируемых альтернатив.
-го эксперта для -й альтернативы. Статистический анализ дает ответ на вопрос о том, есть ли какая-то согласованность (или связь) между упорядочениями анализируемых альтернатив.
Рассмотрим случай оценки связи между ранжировками двух экспертов  -м и
-м и  -м экспертами
-м экспертами  . В этих задачах мерой взаимосвязи может служить коэффициент ранговой корреляции, например, Спирмена.
. В этих задачах мерой взаимосвязи может служить коэффициент ранговой корреляции, например, Спирмена.
Представим вычисление коэффициента ранговой корреляции Спирмена в виде следующего алгоритма.
1. Выполнить ранжирование оцениваемых альтернатив двумя экспертами:
где  – векторы рангов, выставляемых соответственно
– векторы рангов, выставляемых соответственно  -м и
-м и  -м экспертами.
-м экспертами.
2. Вычислить коэффициент ранговой корреляции Спирмена :
143

где  — показатель связанных рангов в i-й ранжировке;
— показатель связанных рангов в i-й ранжировке;  – число групп равных рангов в -й ранжировке;
– число групп равных рангов в -й ранжировке;  – число равных рангов в
– число равных рангов в  -й группе связанных рангов в
-й группе связанных рангов в  -й ранжировке.
-й ранжировке.
Коэффициент корреляции Спирмена изменяется от –1 до +1. Равенство единице достигается при одинаковых ранжировках, те. когда  . Значение
. Значение  имеет место при противоположных ранжировках. При равенстве коэффициента корреляции нулю ранжировки считаются линейно независимыми.
имеет место при противоположных ранжировках. При равенстве коэффициента корреляции нулю ранжировки считаются линейно независимыми.
Проверка статистически значимого отличия от нуля рангового коэффициента корреляции проводится при «не слишком малых» n (n > 10) и заданном уровне значимости критерия а с помощью неравенства
где |
-ная точка распределения Стьюдента с |
степенями свободы; |
(табл. 1П, Приложение). |
Выполнение неравенства (4) приводит к необходимости |
|
отвергнуть гипотезу об отсутствии статистически значимой ранговой корреляционной связи.
Вслучае небольших объемов выборок при
 статистическая проверка гипотезы об отсутствии ранговой корреляционной связи проводится с помощью специальных таблиц. Таблица 2П (см. Приложение) значений
статистическая проверка гипотезы об отсутствии ранговой корреляционной связи проводится с помощью специальных таблиц. Таблица 2П (см. Приложение) значений
вспомогательной величины |
позволяет |
при |
малых |
|
построить то пороговое значение |
, |
при |
превышении |
|
которого по абсолютной величине коэффициентом Спирмена  , следует признать наличие статистически значимой связи между сравниваемыми ранжировками (отвергается гипотеза об отсутствии корреляционной связи). Задавшись уровнем значимости критерия а и числом сравниваемых альтернатив ,
, следует признать наличие статистически значимой связи между сравниваемыми ранжировками (отвергается гипотеза об отсутствии корреляционной связи). Задавшись уровнем значимости критерия а и числом сравниваемых альтернатив ,
определяем |
из |
табл. |
2П |
|
величину |
, |
соответствующую |
заданному |
и |
значению |
(или |
||
приблизительно равному |
). Тогда |
|
|
|||
|
|
|
144 |
|
|
|
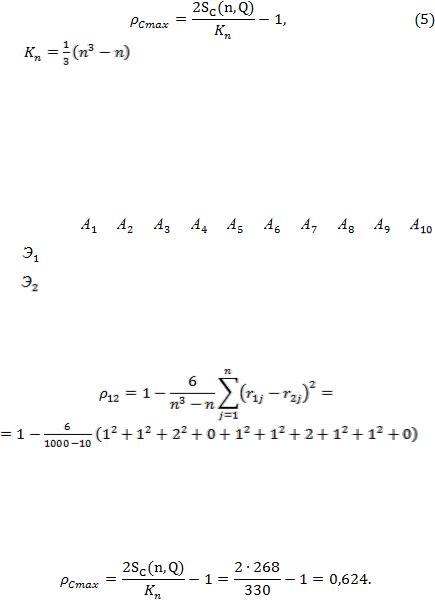
где |
. |
Пример. Два эксперта провели ранжирование 10 альтернатив (табл. 2.3). Вычислить коэффициент ранговой корреляции Спирмена.
Таблица 2.3 Ранжировка 10 альтернатив двумя экспертами
Эксперт |
|
Альтернатива (режимный параметр) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
1 |
4 |
6 |
5 |
9 |
7 |
8 |
10 |
|
|
|
|
|
|
|
|
|
|
|
В данном примере  , связанные ранги отсутствуют
, связанные ранги отсутствуют  . Вычислим выборочный коэффициент корреляции Спирмена:
. Вычислим выборочный коэффициент корреляции Спирмена:
=
= 0,915
Определим значимость полученной оценки при  . При
. При  (величина определена по табл. 2П),
(величина определена по табл. 2П),  по формуле (5) получим
по формуле (5) получим
Поскольку выборочное значение коэффициента ранговой корреляции Спирмена превышает пороговое значение
145
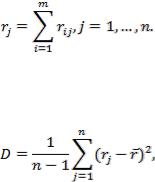
( ), то следует признать наличие статистически значимой связи между сравниваемыми ранжировками (отвергается гипотеза об отсутствии корреляционной связи) и оценка коэффициента ранговой корреляции Спирмена является значимой.
), то следует признать наличие статистически значимой связи между сравниваемыми ранжировками (отвергается гипотеза об отсутствии корреляционной связи) и оценка коэффициента ранговой корреляции Спирмена является значимой.
Перейдем к рассмотрению вопросов оценки согласованности мнений экспертов, когда число экспертов больше двух.
При ранжировании альтернатив эксперты обычно расходятся во мнениях. В связи с этим возникает необходимость в количественной оценке степени согласия экспертов. Получение количественной меры согласованности мнений экспертов позволяет более обоснованно интерпретировать причины расхождения мнений. В качестве меры согласованности мнений группы экспертов часто используют дисперсионный коэффициент конкордации (или согласованности) Кэндалла и энтропийный коэффициент конкордации.
Коэффициент конкордации Кэндалла. Пусть  – матрица результатов ранжирования, полученная в результате оценки
– матрица результатов ранжирования, полученная в результате оценки  альтернатив
альтернатив 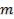 экспертами, т. е.
экспертами, т. е.  – ранг, присеваемый i-м экспертом -й альтернативе.
– ранг, присеваемый i-м экспертом -й альтернативе.
Составим суммы рангов по каждому столбцу. В результате получим вектор с компонентами
Величины  рассмотрим как реализации случайной величины и найдем оценку дисперсии. Как известно, оптимальная по критерию минимума средней квадратической ошибки оценка дисперсии определяется формулой:
рассмотрим как реализации случайной величины и найдем оценку дисперсии. Как известно, оптимальная по критерию минимума средней квадратической ошибки оценка дисперсии определяется формулой:
где  оценка математического ожидания:
оценка математического ожидания:
146
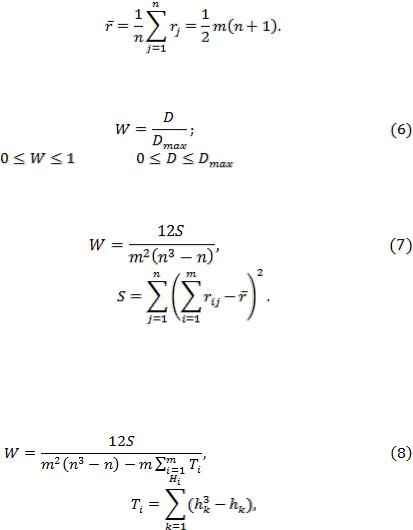
Дисперсионный коэффициент конкордации равен отношению оценки дисперсии к максимальному значению этой оценки:
где |
, так как |
. |
|
Для случая отсутствия связанных рангов (все |
|||
альтернативы |
разные) |
дисперсионный |
коэффициент |
конкордации определяют по формуле Кэндалла |
|
||
Если в ранжировках имеются связанные ранги, то максимальное значение дисперсии в знаменателе формулы (7) становится меньше, чем при отсутствии связанных рангов. При наличии связанных рангов дисперсионный коэффициент конкордации вычисляется по следующей формуле:
где  – показатель связанных рангов в i-й ранжировке;
– показатель связанных рангов в i-й ранжировке;  – число групп равных рангов в -й ранжировке;
– число групп равных рангов в -й ранжировке;  — число равных рангов в
— число равных рангов в  -й группе связанных рангов в
-й группе связанных рангов в  -й ранжировке.
-й ранжировке.
Если совпадающих рангов нет, то  и, следовательно,
и, следовательно,  . В этом случае формула (8) совпадает с формулой (7).
. В этом случае формула (8) совпадает с формулой (7).
147

Коэффициент конкордации  равен единице, если все ранжировки экспертов одинаковы, и равен нулю, если все ранжировки различны, т.е. совершенно нет совпадения.
равен единице, если все ранжировки экспертов одинаковы, и равен нулю, если все ранжировки различны, т.е. совершенно нет совпадения.
Коэффициент конкордации, вычисляемый по формуле
(7) или (8), является выборочной оценкой истинного (теоретического) значения коэффициента и, следовательно, представляет собой случайную величину. Для определения значимости оценки коэффициента конкордации необходимо знать распределение частот для разных значений числа экспертов m и количества альтернатив п.
Для малых значений  (
( ) с помощью табл. 3П-6П значений
) с помощью табл. 3П-6П значений  , приведенных в Приложении, где
, приведенных в Приложении, где
может быть получен ответ па вопрос о том, как сильно могут отклоняться от нуля выборочные значения коэффициента конкордации  в ситуации, когда значение теоретического коэффициента конкордации
в ситуации, когда значение теоретического коэффициента конкордации  свидетельствует о полном отсутствии связи между анализируемыми ранжировками.
свидетельствует о полном отсутствии связи между анализируемыми ранжировками.
«Входами» в указанные таблицы является тройка чисел ( ), «выходом» — вероятность
), «выходом» — вероятность  того, что величина
того, что величина  может быть такой, какой она является в рассматриваемой выборке, или большей в условиях отсутствия связи между ранжировками в генеральной совокупности. Если окажется, что эта вероятность меньше принятой величины уровня значимости критерия
может быть такой, какой она является в рассматриваемой выборке, или большей в условиях отсутствия связи между ранжировками в генеральной совокупности. Если окажется, что эта вероятность меньше принятой величины уровня значимости критерия  (например,
(например,  ), т. е.
), т. е.  , то гипотезу об отсутствии связи следует отвергнуть, т. е. признать статистическую значимость анализируемой связи.
, то гипотезу об отсутствии связи следует отвергнуть, т. е. признать статистическую значимость анализируемой связи.
Таблица 7П критических значений коэффициента конкордации  построена несколько иначе. В ней при уровне значимости
построена несколько иначе. В ней при уровне значимости  и в соответствии со «входами» (
и в соответствии со «входами» ( ) даны «критические» значения
) даны «критические» значения  величины
величины  , т. е. такие значения, при превышении которых следует отвергать гипотезу
, т. е. такие значения, при превышении которых следует отвергать гипотезу
148

об отсутствии связей между ранжировками (признавать их статистическую значимость).
Пример. Три эксперта проранжировали пять альтернатив (табл. 2.4). Оценить согласованность мнений экспертов.
Таблица 2.4 Ранжировка пяти альтернатив тремя экспертами
Эксперт |
|
|
Фактор |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
|
3 |
|
1 |
|
5 |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
4 |
|
3 |
|
5 |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
5 |
|
3 |
|
4 |
|
|
|
|
|
|
|
|
|
В данном примере |
|
|
. Вычислим |
и |
||||
Из табл. 6П (см. Приложение) для  при
при  находим
находим  . Если выбрать уровень значимости критерия
. Если выбрать уровень значимости критерия  , то
, то  и гипотезу об отсутствии связи следует отвергнуть, т. е. признать
и гипотезу об отсутствии связи следует отвергнуть, т. е. признать
149
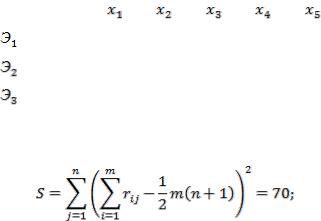
статистическую значимость анализируемой связи и считать, что мнения экспертов согласованны. Если уровень значимости критерия  , то
, то  и гипотезу об отсутствии связи между ранжировками следует принять, считая при этом, что мнения экспертов несогласованны.
и гипотезу об отсутствии связи между ранжировками следует принять, считая при этом, что мнения экспертов несогласованны.
Из табл. 7П (см. Приложение) для  и уровня значимости критерия
и уровня значимости критерия  находим
находим  . Так как
. Так как  , то гипотезу об отсутствии связи между ранжировками следует принять и считать, что мнения экспертов несогласованны.
, то гипотезу об отсутствии связи между ранжировками следует принять и считать, что мнения экспертов несогласованны.
Для уровня значимости критерия  из табл. 7П для
из табл. 7П для  находим
находим  . Так как
. Так как  то и в этом случае гипотезу об отсутствии связи между ранжировками следует принять и считать, что мнения экспертов несогласованны.
то и в этом случае гипотезу об отсутствии связи между ранжировками следует принять и считать, что мнения экспертов несогласованны.
Пример. Пусть три эксперта проранжировали пять альтернатив (табл. 2.5). Требуется оценить согласованность мнений экспертов.
Таблица 2.5 Ранжировка пяти альтернатив тремя экспертами
Эксперт |
|
|
Фактор |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
3 |
|
4 |
|
1,5 |
1,5 |
|
|
|
|
|
|
|
|
|
4 |
2 |
|
5 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
3,5 |
3,5 |
|
5 |
|
2 |
1 |
|
|
|
|
|
|
|
|
В данном примере  и в отличие от предыдущего примера есть связанные ранги. Вычислим
и в отличие от предыдущего примера есть связанные ранги. Вычислим  и
и  :
:
150
