3.3. Алгебраический критерий устойчивости

Проверка устойчивости САУ путем вычисления корней характеристического уравнения (3.5) не всегда возможна из-за высокого порядка решаемых уравнений.

На практике использует алгебраические и частотные критерии устойчивости.

Критерий Гурвица – алгебраический критерий, он позволяет судить об устойчивости САУ на основе анализа коэффициентов характеристического уравнения (3.5).

Система с характеристическим уравнением (3.5) будет устойчивой, если определитель Гурвица _n и все его диагональные миноры_n-1.,_{n-2 , … ,}₁ положительны при а ₀ .

Для того, чтобы найти определитель Гурвица, нужно построить матрицу Гурвица.

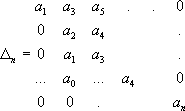(3.8)

Матрица Гурвица заполняется по следующему правилупо столбцам относительно главной диагонали. Сначала выписывают коэффициенты на главную диагональ. Ниже главной диагонали записывают коэффициенты с уменьшением индекса, а выше - с увеличением.

Диагональные миноры рассчитываются так

₁ =| а₁|,

а₁ а₃

₂= а₀ а₂ = а₁а₂ - а₃ а_0, и т.д.

Условием нахождения САУ на границе устойчивости является равенство нулю определителя Гурвица (_n=0), а все остальные диагональные миноры должны быть положительными.

Недостатки критерия Гурвица заключаются в следующем.

1. Для систем при n>5 (более высокого порядка) критерии Гурвица требуют анализа очень громоздких выражений, т.е. при n>5 данный критерий практически не используется.

2. Критерий Гурвица не позволяет выделять неустойчивое звено в системе (определить причину неустойчивости САУ).

3.4. Частотные критерии устойчивости сау

Частотные критерии основаны на изучении связи между формой частотной характеристики САУ и характером распределения корней характеристического уравнения в комплексной плоскости.

Наибольшее применение нашли два критерия устойчивости: критерий Михайлова и критерий Найквиста [2].

Критерий устойчивости Михайлова был предложен в 1938 году. Это графический критерий устойчивости, суть которого заключается в следующем.

Если характеристическое уравнение замкнутой САУ имеет вид

a₀ pⁿ + a₁ p^n-1 + … + a_n-1 p + a_n = 0 , (3.9)

то, представив левую часть равенства (3.9) в виде функции

D(p)= a₀ pⁿ + a₁ p^n-1 + … + a_n-1 p + a_n

и подставив в неё p= j, получим уравнение комплексного вектора

D(j)= a₀ (j) ⁿ + a₁ (j) ^n-1 + … + a_n-1 (j) + a_n.

D(j) задаёт комплексный вектор, который при изменении угловой частоты колебаний  от 0 до  опишет на комплексной плоскости некоторую кривую – годограф, или кривую Михайлова.

Для построения кривой Михайлова необходимо в D(j) выделить действительную и мнимую части:

D(j)= U()+jV(),

где

U() = a _n – a _n-2 ² + a _n-4 ⁴ - …

V() = a _n-1 – a _n-3 ³ + a _n-5 ⁵ a - a _n-7 ⁷ + …

(n-чётное).

Например, при n=8 получим ( с учётом j²=-1 )

D(j)= a₀ (j) ⁸ + a₁ (j) ⁷ + … + a₇(j) + a₈ =

(a₀  ⁸ - a₂  ⁶ + a₄ ⁴ - a₂ ²+ a₈) + j (a₇  - a₅ ³ + a₃ ⁵ - a₁ ⁷).

Далее, задаваясь различными значениями частоты =_1,_2,… вычислим координаты точек годографа D(j): при =0 U()=a _{n ,} V()=0; при  jV().

Рассмотрим случай n=1.

D(p)= a₀ p + a_{1 ,}

D(j)=a₀ (j)+ a_1.

Действительная часть постоянна U(a₁

_{j V n=1}

U

0

a₁

Рис. 3.8

Рассмотрим случай n=2.

D(p)= a₀ p² + a₁p +a_2,

D(j)= a₀(j)² + a₁(j)+ a₂ =[ a₂ -a₀²]+j(a₁)

Действительная часть U(=a₂ -a₀².a₁

Мнимая часть V()=a₁.

При =0 V=0, U= a_2.

П ри =a₂/a₀ U= 0, V=a₁a₂/a₀

Критерий Михайлова формулируется так. Система n-го порядка будет устойчива, если годограф, начинаясь на действительной оси при U, огибает против часовой стрелки

начало координат, проходя последовательно ровно n квадрантов (четвертей комплексной плоскости).

Для устойчивых САУ кривая Михайлова всегда имеет плавную спиралевидную форму, уходящую в бесконечность в том квадранте комплексной плоскости, номер которого соответствует степени n характеристического уравнения системы. Более n квадрантов кривая Михайлова для уравнения n-го порядка пройти не может, поэтому неустойчивость САУ всегда связана с нарушением последовательного обхода квадрантов (рис. 3.9).

_jV

_{n =3}

U

0

a_n

_{Кривые Михайлова для неустойчивой системы}

Рис. 3.9

Условием нахождения САУ на границе устойчивости является прохождение кривой Михайлова через начало координат.

Для оценки устойчивости замкнутой САУ по известной АФЧХ разомкнутой системы используют критерий, предложенный в 1932 году американским учёным Найквистом. При этом исследуемая АФЧХ может быть получена как аналитически, так и экспериментально. Разомкнутая САУ может быть устойчивой, неустойчивой или находиться на границе устойчивости. Если САУ состоит из устойчивых звеньев, то она будет устойчивой в разомкнутом состоянии. При наличии хотя бы одного неустойчивого звена разомкнутая система будет неустойчивой. При наличии в САУ интегрирующего звена система будет находиться на границе устойчивости. Критерий Найквиста формулируется так.Чтобы замкнутая САУ была устойчивой, необходимо и достаточно выполнение следующих условий: при устойчивой разомкнутой САУ, или находящейся на границе устойчивости, АФЧХ при изменении  от  до  не должна охватывать точку с координатами (-1, j0); при неустойчивой разомкнутой САУ АФЧХ должна охватывать точку (-1, j0) столько раз, сколько корней характеристического уравнения разомкнутой САУ лежит справа от мнимой оси комплексной плоскости.

_jV

 =0 U

-1 0

Рис. 3.10

Возможно также определение устойчивости САУ по логарифмическим характеристикам.

Будем оценивать устойчивость САУ по амплитудной логарифмической частотной характеристике L() и по фазовой характеристике ().

Если разомкнутая САУ устойчива, то для устойчивости замкнутой САУ необходимо и достаточно, чтобы во всех областях положительной ЛАХ (L() разность между числом положительных и отрицательных переходов фазовой характеристики () через линию –180⁰ равнялась нулю.

Введём обозначения:

a-точка пересечения L() с осью частот;

b-точка пересечения () с осью частот;

- запас устойчивости по фазе;

l-запас устойчивости по амплитуде.

Если точка a расположена левее точки b, в положительной области ЛАХ число переходов () через линию ()=-180 равно нулю. Система устойчива.

L(),φ(ω)

a b

φ = -180

 l

Рис. 3.11

Если точка b расположена левее точки a, в области положительной ЛАХ есть один переход фазовой характеристики через ось ()=-180, следовательно, система неустойчива.