Учебное пособие 800319

М.Л. Лапшина С.А. Фурсова М.В. Юрьева

РЯДЫ. РЯДЫ ФУРЬЕ

Учебное пособие

Часть 1

Воронеж 2004

3

4

ВВЕДЕНИЕ

Учебное пособие «Ряды» посвящено одному из важнейших разделов математического анализа – теории рядов и предназначено для студентов 1 курса инженерных специальностей, изучающих курс «Математика» раздел «Ряды».

В каждой области точного естествознания наряду с главами, освещающими важнейшие понятия и закономерности данной области, имеются и такие разделы, которые посвящены созданию и изучению специальной аппаратуры, служащей для овладения изучаемым предметом; значение таких разделов не столько принципиальное, сколько техническое; и тем не менее методологическая важность их бывает настолько велика, что без их систематического изложения невозможно никакое цельное построение соответствующей теории.

Теория рядов в отношении к основным понятиям и важнейшим закономерностям математического анализа играет роль такого технического орудия, вспомогательного аппарата; и тем не менее, многочисленными и разнообразными применениями этого аппарата настолько проникнуто все здание как самого анализа, так и большинства опирающихся на его основы прикладных наук, что теории рядов следует отдать центральное место в арсенале методов современной математики. Поэтому ни один курс математического анализа не может обойтись без систематического изложения этого раздела.

7

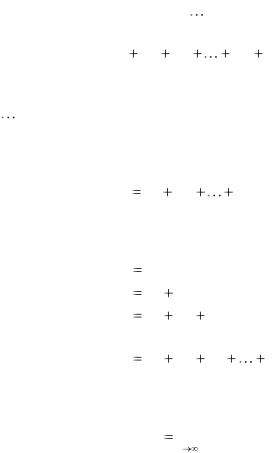
ГЛАВА 1 РЯДЫ

1.1. Ряд. Сумма ряда

Определение 1. Пусть задана бесконечная последовательность чисел

u1 , u 2 , , u n ,... называются членами ряда.

Определение 2. Сумма конечного числа n первых членов ряда называется n-й частичной суммой ряда:

Рассмотрим частичные суммы

Если существует конечный предел

S lim Sn ,

n

8

то его называют суммой ряда (1.1) и говорят, что ряд схо-

дится.

n 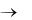), то говорят, что ряд (1.1) расходится и суммы не имеет.

Теорема 1. Если сходится ряд, получившийся из данного ряда (1.1) отбрасыванием нескольких его членов, то сходится и сам данный ряд. Обратно, если сходится данный ряд, то сходится и ряд, получившийся из данного отбрасыванием нескольких членов.

Иными словами, на сходимость ряда не влияет отбрасывание конечного числа его членов.

1.2. Необходимый признак сходимости ряда

Теорема. Если ряд сходится, то его n-й член стремится к нулю при неограниченном возрастании n.

Следствие. Если n-й член ряда не стремится к нулю при n 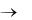, то ряд расходится.

Пример. Ряд

расходится, так как

Подчеркнем, что рассмотренный признак является только необходимым, но не является достаточным, т.е. из

9

Пример. Ряд

расходится, так как его члены (начиная со второго) больше соответствующих членов гармонического ряда

который, как известно, расходится.

1.4. Признак Даламбера

Теорема (признак Даламбера). Если в ряде с положительными членами

отношение (n+1)-го члена к n-му при n 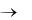имеет конечный предел l, т.е.

то:

1)ряд сходится в случае l<1,

2)ряд расходится в случае l>1.

(В случае l=1ответа на вопрос о сходимости или расходимости ряда теорема не дает)

11

Пример. Исследовать сходимость ряда

Ряд сходится.

1.5. Признак Коши

Теорема (признак Коши). Если для ряда с положительными членами

12