
Учебное пособие 800319
.pdf
1)ряд сходится в случае l<1,
2)ряд расходится в случае l>1.
Пример. Исследовать сходимость ряда
1 |
2 |
2 |
3 |
3 |
n |
|
n |
|
|
|
|
|
|
... |
|
|
... . |
|
|
|
|
|
|
|
||
3 |
5 |
|
7 |
|
2n |
1 |
||
Решение: Применим признак Коши:
|
|
|
|
n |
n |
|
n |
1 |
|
|
|
|
|
|
|
|
1 . |
||||
lim n u |
n |
lim n |
|
lim |
||||||
|
|
|
|
|
||||||
(2n 1) |
|
2n 1 |
2 |
|||||||
n |
n |
|
n |
|
||||||
|
|
|
||||||||
|
|
|
|
|
|
|
||||
Ряд сходится.
Замечание. Как и в признаке Даламбера, случай
lim n u |
n |
l 1 |
n |
|
|
|
|
требует дополнительного исследования.
1.6. Интегральный признак сходимости ряда
Теорема. Пусть члены ряда
u1 u 2 u 3 |
u n ... |
(1.9) |
положительны и не возрастают, т.е.
u1 u 2 u 3 ..., |
(1.9`) |
13

и пусть f(x) – такая непрерывная невозрастающая функция, что
|
f (1) u1 , f (2) u2 , …, |
f (n) un , (1.10) |
тогда, справедливы следующие утверждения: |
||
1) |
если несобственный интеграл |
f (x)dx сходится, то |
1
сходится и ряд (1.9); 2) если указанный интеграл расходится, то расходится и ряд (1.9).
1.7. Знакочередующиеся ряды. Теорема Лейбница
До сих пор мы рассматривали ряды, члены которых положительны. В этом параграфе будем рассматривать ряды, члены которых имеют чередующиеся знаки, т.е. ряды вида
u1 u 2 u 3 u4 ... ,
где u1 , u 2 , , u n ,... положительны.
Теорема Лейбница. Если в знакочередующемся ряде
u1 u 2 |
u 3 |
u4 |
... (un 0) |
(1.11) |
члены таковы, что |
|
|
|
|
u1 |
u 2 |
u 3 |
..., |
|
и |
|
|
|
|
lim un |
0 |
|
|
|
n |
|
|
|
|
14

то ряд (1.11) сходится, его сумма положительна и не превосходит первого члена.
Пример 1. Ряд
1 |
1 |
1 |
|
1 |
... |
||
|
|
|
|
|
|||
2 |
3 |
4 |
|||||
|
|
||||||
сходится, так как
1) 1 12 13 ... ;
2) |
lim un |
lim 1n |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сумма n первых членов ряда |
|
|
|
|
|||||||||||||||
|
|
sn |
1 |
|
1 |
|
1 |
|
|
1 |
... |
( 1) |
n 1 1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
3 |
4 |
|
n |
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
отличается |
от суммы ряда |
s |
на |
величину, меньшую |
||||||||||||||||
1 |
n 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
1 |
|
|
1 |
|
1 |
|
... |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2! |
|
3! |
4! |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
сходится в силу теоремы Лейбница.
1.8. Знакопеременные ряды. Абсолютная и условная сходимость
Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.
Рассмотренные в предыдущем параграфе знакоче-
редующиеся ряды являются, очевидно, частным случаем
знакопеременных рядов.
15

Теорема 1. Если знакопеременный ряд
u1 u 2 |
u n ... |
таков, что ряд, составленный из абсолютных величин его членов,
u1 |
|
u 2 |
|
u n |
... , |
сходится, то и данный знакопеременный ряд также сходится.
Определение. Знакопеременный ряд
u1 u 2 u 3 |
u n ... |
(1.12) |
называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов:
u1 |
|
u 2 |
|
u 3 |
|
u n |
... . (1.13) |
Если же знакопеременный ряд (1.12) сходится, а ряд (1.13), составленный из абсолютных величин его членов, расходится, то данный знакопеременный ряд (1.12) называется условно или неабсолютно сходящимся рядом.
Пример. Знакопеременный ряд 1 |
1 |
|
1 |
|
1 |
... явля- |
|
|
|
||||
|
2 |
3 |
4 |
|
||
ется условно сходящимся, так как ряд, составленный из аб-
солютных |
|
величин его членов, есть гармонический |
||||
ряд1 |
1 |
|
1 |
|
1 |
... , который расходится. Сам же ряд схо- |
|
|
|
||||
|
2 |
|
3 |
4 |
|
|
дится, что легко проверить с помощью признака Лейбница.
16

1.9. Функциональные ряды
Ряд
u1 u 2 |
u n ... |
называется функциональным, если его члены являются функциями от x.
Рассмотрим функциональный ряд
u1 (x) u 2 (x) u 3 (x) |
u n (x) ... (1.14) |
Давая x определенные числовые значения, мы получаем различные числовые ряды, которые могут оказаться сходящимися или расходящимися.
Совокупность тех значений x, при которых функциональный ряд сходится, называют областью сходимости этого ряда.
Очевидно, что в области сходимости ряда его сумма является некоторой функцией от x. Поэтому сумму функционального ряда обозначают через s(x).
Пример. Рассмотрим функциональный ряд
1 x x2 ... xn ...
этот ряд сходится при всех значениях x в интервале (-1,1), т.е. при всех x, удовлетворяющих условию x 1 . Для каждого значения x в интервале (-1,1) сумма ряда рав-
1
на 1 x (сумма убывающей геометрической прогрессии со
17

знаменателем x). Таким образом, в интервале (-1,1) данный ряд определяет функцию
|
|
s(x) |
|
|
1 |
, |
|
|
|
|
|
|
|||
|
|
1 |
x |
||||
которая является суммой ряда, т.е. |
|
|
|||||
1 |
1 x |
x2 |
x3 ... . |
||||
|
|
||||||
1 x |
|||||||
|
|
|
|
|
|||
Обозначим через sn (x) сумму первых n членов ряда (1.14). Если этот ряд сходится и сумма его равна s(x), то
s(x) sn (x) rn (x) ,
где rn (x) есть сумма ряда u n 1 (x) |
u n 2 (x) ..., т.е. |
|
rn (x) u n |
1 (x) u n |
2 (x) ... . |
В этом случае величина |
rn (x) называется остатком ряда |
|
(1.14). Для всех значений x в области сходимости ряда |
|
имеет место соотношение lim sn (x) s(x) , поэтому |
|
|
n |
lim rn (x) |
lim s(x) sn (x) 0 , |
n |
n |
т.е. остаток rn (x) сходящегося ряда стремится к нулю при n  .
.
18

1.10. Мажорируемые ряды
Определение. Функциональный ряд
u1 (x) u 2 (x) u 3 (x) |
u n (x) ... |
называется мажорируемым в некоторой области изменения x, если существует такой сходящийся числовой ряд
1 |
2 |
3 |
... |
n |
... |
|
|
с положительными членами, что для всех x из данной области выполняются соотношения
u1 (x)
 1 , u2 (x)
1 , u2 (x)
 2 , …, un (x)
2 , …, un (x)
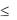 n ,… .
n ,… .
Иначе говоря, ряд называется мажорируемым, если каждый его член по абсолютной величине не больше соответствующего члена некоторого сходящегося числового ряда с положительными членами.
Например, ряд
cos x |
|
cos2x |
|
cos3x |
... |
cosnx |
... |
|
|
|
|
|
|
|
|||
1 |
22 |
32 |
n2 |
|||||
|
|
|||||||
есть ряд, мажорируемый на всей оси Ox. Действительно, для всех значений x выполняется соотношение
cosnx |
1 |
(n =1, 2,…) , |
|
|
|
|
|
n2 |
|
n2 |
|
|
|
||
19

а ряд
1 |
1 |
1 |
... |
, |
|||
|
|
|
|
|
|||
1 |
22 |
32 |
|||||
|
|
||||||
как известно, сходится.
Непосредственно из определения следует, что ряд, мажорируемый в некоторой области, абсолютно сходится во всех точках это области (см. п.1.8). Кроме того, мажорируемый ряд обладает еще следующим важным свойством.
Теорема. Пусть функциональный ряд
u1 (x) u 2 (x) |
u n (x) ... |
мажорируем на отрезке [a, b]. Пусть s(x) – сумма этого ряда, sn (x) - сумма n первых членов этого ряда. Тогда для каждого как угодно малого числа  0 найдется положи-
0 найдется положи-
тельное N такое, что при всех n |
|
N будет выполняться не- |
|
равенство |
|
|
|
|
s(x) sn (x) |
|
, |
|
|
||
какова бы ни было x из отрезка [a, b].
1.11. Степенные ряды. Интервал сходимости
Определение 1. Степенным рядом называется функциональный ряд вида
a |
0 |
a x |
a |
2 |
x2 |
... a |
n |
xn |
... , |
|
1 |
|
|
|
|
|
20

где a0 , a1 , a2 ,..., an ,... - постоянные числа, называемые ко-
эффициентами ряда.
Областью сходимости степенного ряда всегда является некоторый интервал, который, в частности, может вырождаться в точку.
Теорема 1. (теорема Абеля).
1) Если степенной ряд сходится при некотором значении x0 , не равном нулю, то он абсолютно сходится при
всяком x, для которого x
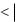 x0 ;
x0 ;
2) если ряд расходится при некотором значении x 0' , то он расходится при всяком x, для которого x
 x0' .
x0' .
Теорема 2. Областью сходимости степенного ряда является интервал с центром в начале координат.
Определение 2. Интервалом сходимости степенного ряда называется такой интервал от –R до +R, что для всякой точки x, лежащей внутри этого интервала, ряд сходится и притом абсолютно, а для точек x, лежащих вне его, ряд расходится. Число R называют радиусом сходимости степенного ряда.
Пусть имеем ряд
a |
0 |
a x |
a |
2 |
x2 |
... a |
n |
xn |
... . (1.15) |
|
1 |
|
|
|
|
|
Рассмотрим ряд, составленный из абсолютных величин его членов:
|
a |
0 |
|
a |
|
x |
|
a |
2 |
|
|
|
x |
|
2 |
|
a |
3 |
|
|
|
x |
|
3 ... |
|
a |
n |
|
|
|
x |
|
n |
... . (1.16) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для определения сходимости последнего ряда (с положительными членами!) применим признак Даламбера.
21

Допустим, что существует предел
lim |
un 1 |
lim |
an 1 xn 1 |
lim |
an 1 |
|
|
x |
|
L |
|
x |
|
. |
||
|
|
|
|
|
||||||||||||
un |
an x |
n |
an |
|||||||||||||
n |
n |
n |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда по признаку Даламбера ряд (1.16) сходится, если
|
L |
|
x |
|
|
1, т.е. если |
x |
1 L , и расходится, если L |
x |
1, т.е. |
|||||||||||
если |
|
x |
|
1 L . |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
Следовательно, ряд (1.15) сходится абсолютно при |
|||||||||||||||
|
x |
|
1 L . Если же |
|
x |
|
1 L , то lim |
un |
1 |
|
x |
|
L 1 , и ряд (1.16) |
||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
un |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
расходится.
Из предыдущего следует, что интервал 1 L , 1
L , 1 L есть интервал сходимости степенного ряда (1.15), т.е.
L есть интервал сходимости степенного ряда (1.15), т.е.
R |
1 |
lim |
an |
|
. |
|
L |
an |
1 |
||||
|
n |
|
||||
|
|
|
|
|
||
|
|
|
|
|
|
Аналогичным образом для определения интервала сходимости можно пользоваться признаком Коши, и тогда
R |
1 |
|
|
|
|
|
. |
|
|
|
|
|
|
||
|
|
|
|
|
|
||
lim n |
|
a |
|
||||
|
|
n |
|
|
|||
|
n |
|
|
|
|
|
|
Пример 1. Определить интервал сходимости ряда
1 x x2 x3 ... xn ... .
22
