Напряжение при изгибе прямого бруса

П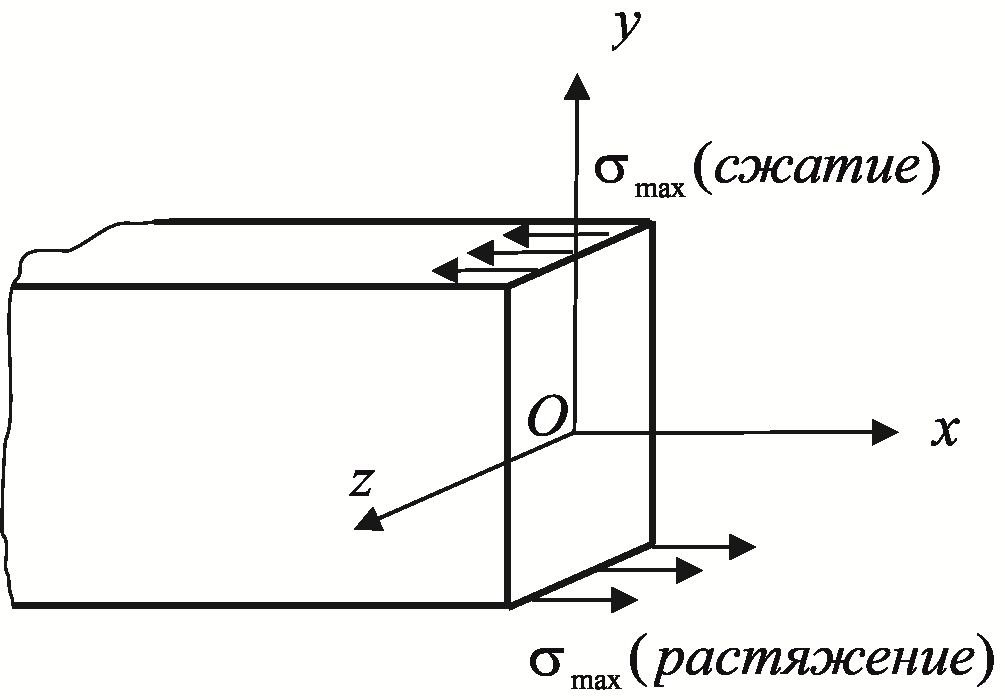 ри изгибе максимальные нормальные напряжения возникают в нижних (растяжение) и верхних (сжатие) волокнах.

При этом , где - изгибающий момент, - осевой момент инерции.

Величина называется моментом сопротивления при изгибе

.

Следовательно, . ( , , ).

Расчет балки на прочность

Первый тип. Задана балка, нагрузка на балку и расчетное сопротивление. Требуется подобрать сечение балки.

Вначале определяют опорные реакции и строят эпюры изгибающих моментов и поперечных сил. По максимальному изгибающему моменту и расчетному сопротивлению определяют требуемый момент сопротивления

.

По сортаменту проката (сортаментом проката называется совокупность профилей и их размеров) подбирают соответствующее сечение с некоторым запасом. Затем строят эпюру изгибающих моментов и поперечных сил от собственного веса и определяют максимальное напряжение с учетом собственного веса. Оно должно быть меньше расчетного сопротивления.

.

Второй тип. Задана балка, дали нагрузки и известно сечение. Требуется найти наибольшее нормальное напряжение в опасном сечении балки.

Сначала определяют опорные реакции и строят эпюры и . Затем по максимальному изгибающему моменту и моменту сопротивлению определяют наибольшее напряжение, которое должно быть меньше расчетного сопротивления.

.

Третий тип. Задана балка, сечение балки и тип нагрузки (например, равномерно распределенная). Нужно определить расчетную нагрузку (несущую способность балки).

По виду и размерам сечения определяют момент сопротивления и находят

.

Зная характер загружения балки, можно установить зависимость между нагрузкой и наибольшим изгибающим моментом и определить затем расчетную нагрузку. После расчета балки проверяют касательные напряжения в сечении, где поперечная сила максимальна.

Кручение

Кручение возникает при действии на брус пары сил в плоскости, перпендикулярной к оси вала. Момент пары называется крутящим моментом.

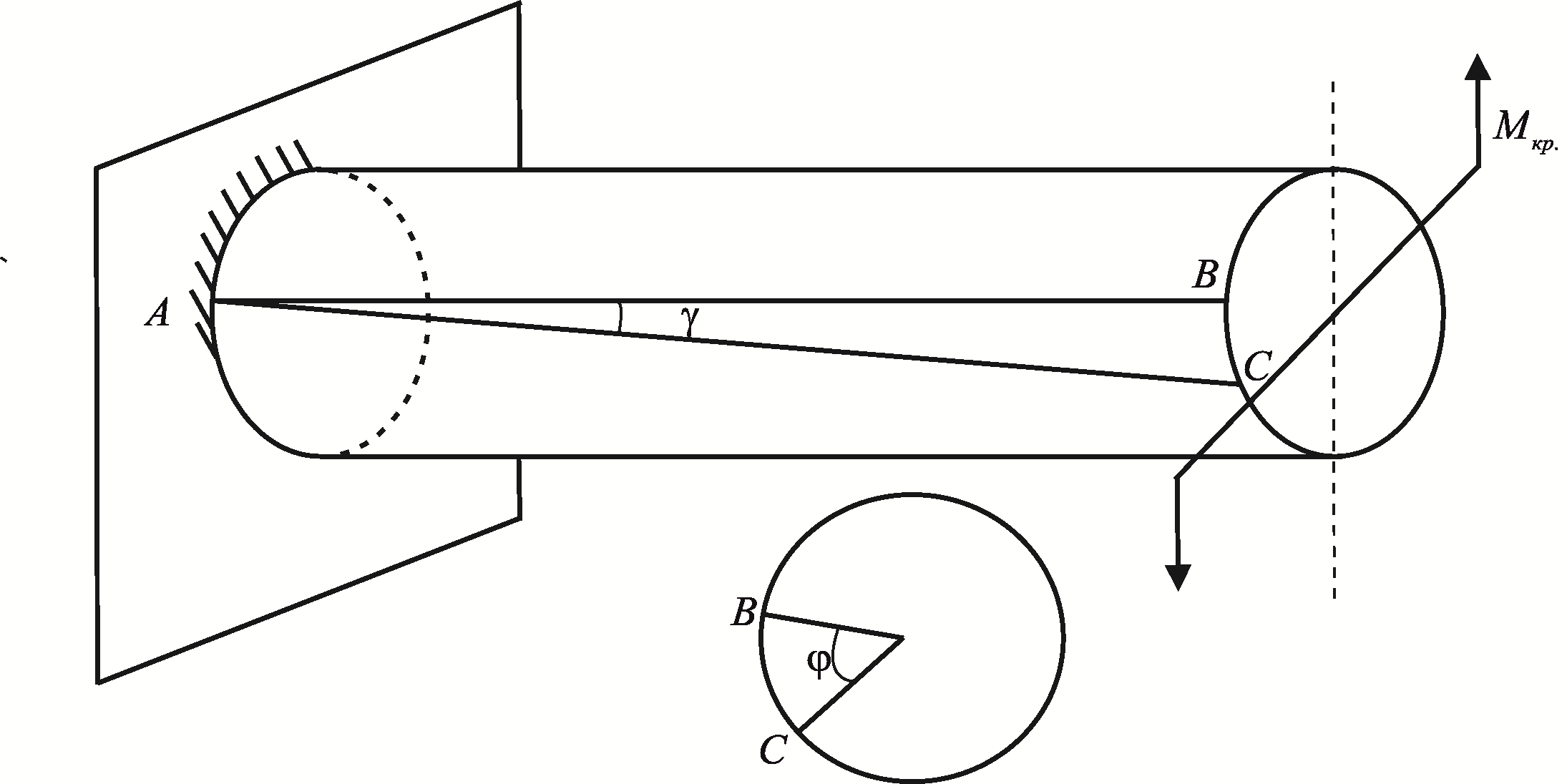
Рис. 40

При кручении брус деформируется, смежные сечения бруса поворачиваются относительно друг друга, образующая искривляется, переходя в положения . При этом допустимы следующие предположения:

1) ось бруса не деформируется;

2) поперечные сечения, плоские до деформации, остаются плоскими и после деформации;

3) продольные волокна не изменяют своей длины;

4) радиусы поперечных сечений остаются прямыми после деформации, поворачиваясь на некоторый угол.

Из этих предположений следует, что при кручении в брусе возникают напряжения чистого сдвига, т.е. в поперечном сечении отсутствуют нормальные напряжения, а возникают только касательные. При этом максимальные касательные напряжения

,

г де - радиус вала, - полярный момент инерции сечения относительно центра ( - площадь узкого кольца радиуса ).

Моментом сопротивления при кручении называется величина , тогда .

При расчете валов на кручении, максимальное касательное напряжение должно быть меньше расчетного сопротивления на срез для материала вала, т.е. .