Метод сечений
Для определения внутренних сил, возникающих при деформации тела, пользуются методом сечений (разрезов). Он заключается в том, что тело, подверженное действию внешних сил, рассекают и рассматривают равновесия отсеченной части.
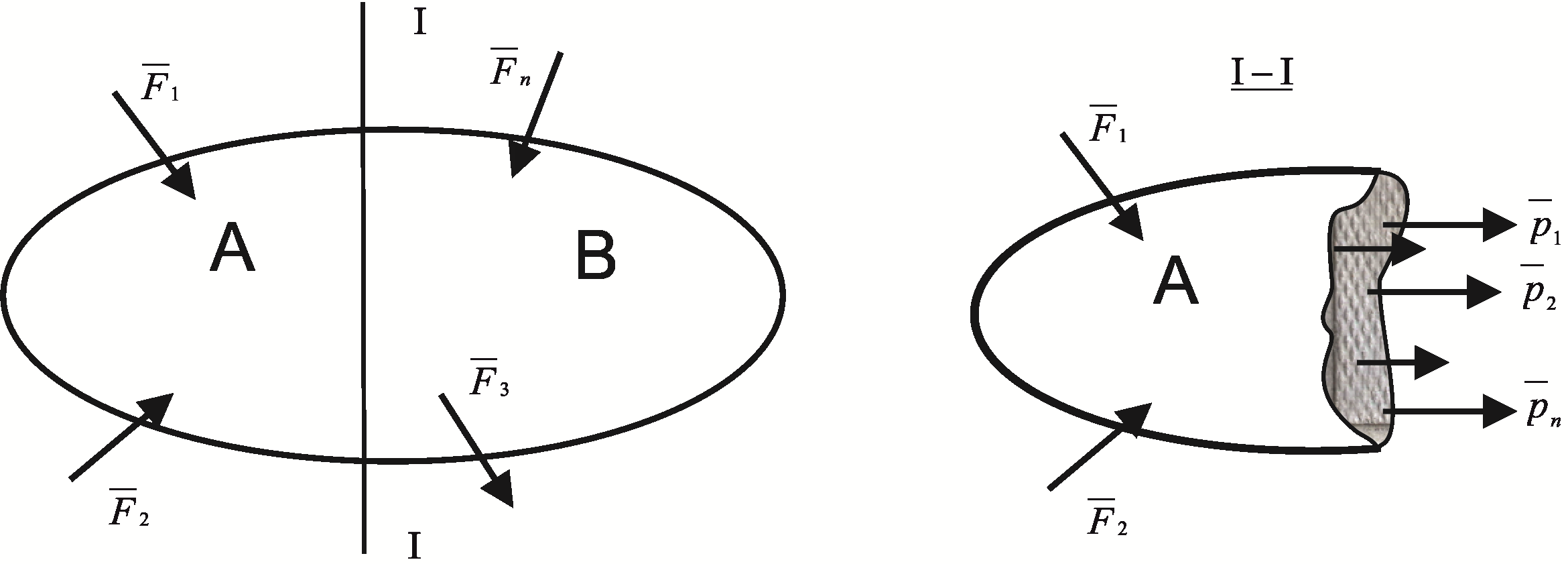
Рис. 32
,
,…,
-
система внешних сил, которая является
уравновешенной,
,
,…,
- система внутренних сил. Составляя
уравнения равновесия действующих на
часть A
внешних сил
,
и внутренних сил
,
,…,
,
определим внутренние силы, действующие
в любой точке площади сечения.
Внутренняя
сила, действующая на единицу площади
сечения, называется напряжением. Если
- равнодействующая всех внутренних сил
,
,…,
,
а
- площадь сечения, по которой
распределили равномерно, то напряжение
(
,
).
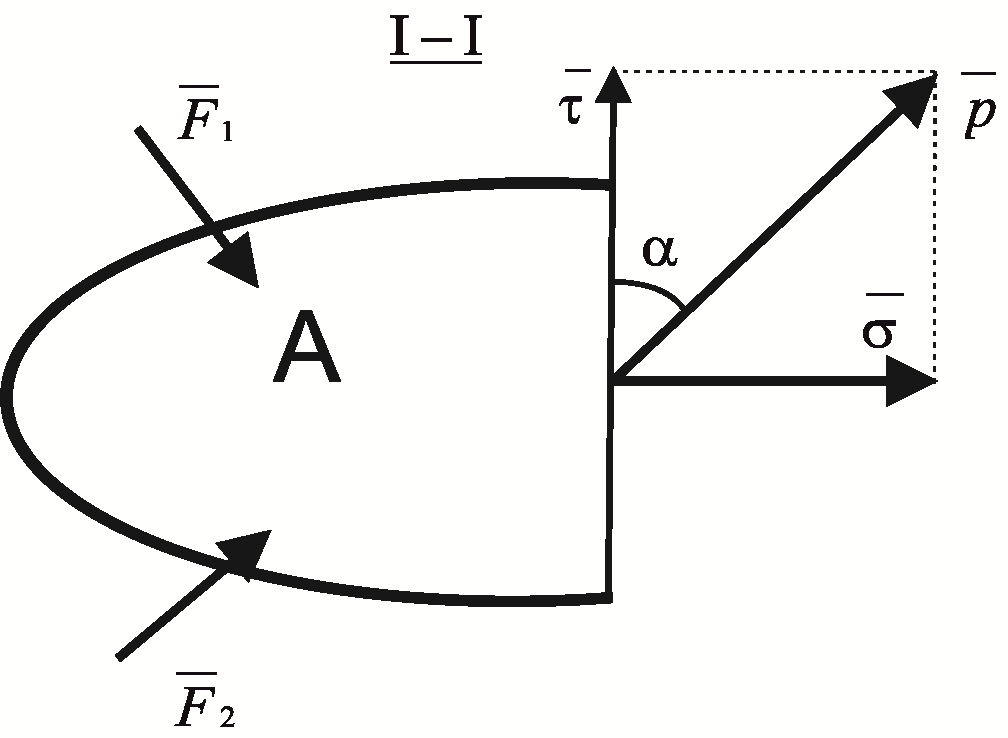
Рис. 33
Если
образует угол
с плоскостью сечения
,
то его можно разложить на две составляющие
,
,
где
- нормальное напряжение,
- касательное напряжение.
Растяжение и сжатие
Рассмотрим
стержень, растянутый силами
и
.
Рис. 34
Применим метод сечений, отбросим правую часть стержня, заменив её действие на левую часть внутренними силами с равнодействующей . Из условия равновесия
Т.к. из опыта, при действии силы вдоль оси стержня вся его продольные волокна удлиняются одинаково, то внутренние силы распределены равномерно по всей площади сечения. Тогда возникающие в сечении нормальные напряжения
.
При
растяжении (сжатия) общая длина стержня
увеличивается (уменьшается) на
.
Величина
(
- длина стержня до деформации)
называется относительной продольной деформацией при растяжении (сжатии) прямого бруса.
Английский
ученый Роберт Гук установил опытным
путем линейную зависимость между
и
,
пока имеют место упругие деформации
(закон Гука)
,
где
(Па или Н/м2)
– модуль упругости, характеризующий
способность материала сопротивляться
деформациям.
Кроме
продольной деформации прямого бруса
при растяжении (сжатия) происходит и
его поперечная деформация. Пусть ширина
его уменьшается на
.
Тогда относительная поперечная деформация
(
- первоначальная ширина бруса).
Коэффициентом Пуассона называется величина
.
Это
безразмерная величина, лежащая в пределах
от
до
.
Расчет по допускаемым напряжениям и предельным состояниям
1)
По допускаемым
напряжениям:
максимальное напряжение, возникающее
в элементе, должно быть меньше допускаемого.
Коэффициент, показывающий, во сколько
допускаемое напряжение меньше предельного,
называют коэффициентом запаса
.
Допускаемые напряжения
,
.
Величина коэффициента запаса зависит от вида внешней нагрузки и от условий работы рассматриваемого элемента конструкции.
2) По предельным состояниям: здесь расчет конструкций ведут по трем предельным состояниям – а) по несущей способности; б) по деформациям, если они могут нарушить нормальную эксплуатацию конструкции; в) по образованию и раскрытию трещин (для железобетонных и каменных конструкции). Здесь вместо одного коэффициента вводят три:
-
коэффициент перегрузки
учитывает возможные отклонения нагрузки
от нормативных значений, при этом за
расчетную нагрузку принимают
;
-
коэффициент условий работы
характеризует изменения, возникающие
при эксплуатации сооружения или
конструктивного элемента (возможное
ослабление поперечного сечения
отверстиями, влияние среди и т.д.);
-
коэффициент однородности материала
учитывает возможные изменения свойств
материала конструкции по сравнению с
нормативными. При этом, расчетные
сопротивление материала
Коэффициенты , , для различных материалов даны в нормах по расчету строительных конструкций.
Задача
10. Заданы
внешние силы:
,
,
;
площади поперечных сечений стального
стержня по участкам и их длины (рис. 35
a):
,
,
,
,
.
Требуется
найти нормальные напряжения
;
перемещения сечений
и построить эпюры продольной силы
,
и
.
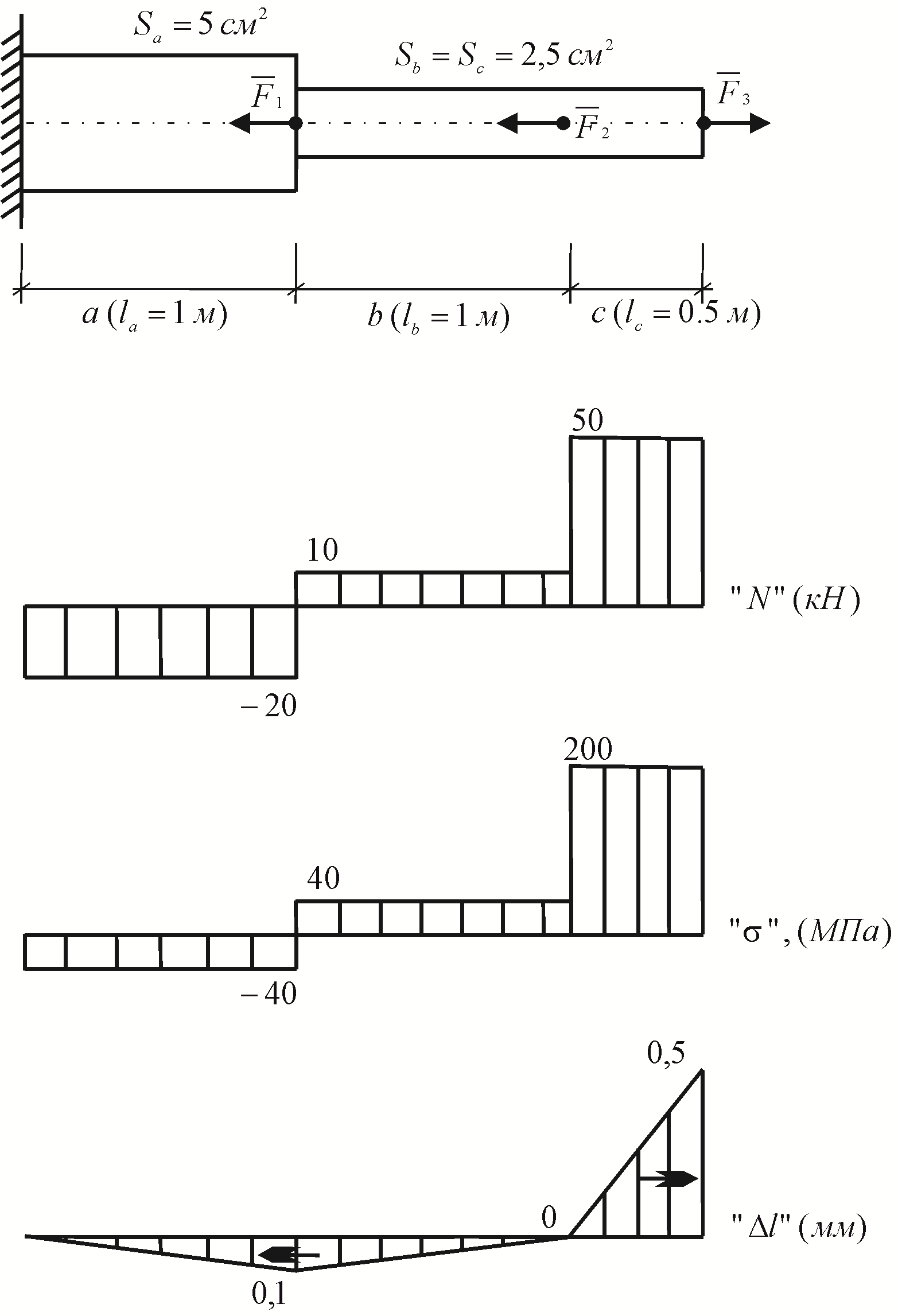
Рис. 35
Решение. Определять реакцию в заделке нет смысла, так как при вычислении в любом сечении продольной силы берем внешние силы только справа от сечения (со стороны свободного конца).
Правила построения эпюры продольной силы :
Продольная сила в произвольном сечении стержня равна алгебраической сумме проекций всех внешних сил, взятых по одну сторону от сечения, на продольную ось.
Правила знаков: сила, направленная от сечения, берется со знаком плюс; сила, направленная на сечение, берется со знаком минус.
Штриховка на эпюре всегда должна быть перпендикулярна продольной оси стержня, а значит, и оси эпюры.
Ординаты эпюр, отложенные в выбранном масштабе, должны сопровождаться числовой характеристикой, а поле эпюры – знаком.
Скачки на эпюре должны быть равны значениям внешних сосредоточенных сил, приложенных в соответствующих сечениях.
Таким образом, продольные силы в поперечных сечениях стержня на участках «с», «b» и «a» будут равны соответственно (Рис. 35):
(растяжение);
(растяжение);
(сжатие).
Нормальные напряжения в произвольном поперечном сечении стержня определяются по формуле
где - продольная сила; - площадь поперечного сечения.
Следовательно, нормальные напряжения на участках «a», «b» и «с» равны соответственно:
(сжатие),
(растяжение),
(растяжение).
Абсолютное удлинение участка стержня длиной определяется по закону Гука:
,
где
- модуль упругости (для стали -
).
Абсолютные удлинения по участкам:
(укорочение);
(удлинение);
(удлинение).
Для построения эпюры вычисляем перемещения необходимых точек, т. е. суммарное удлинение (укорочение) соответствующего участка, считая от заделки.
(влево),
так как участок «a»
укоротился, а его левая точка – неподвижна;
;
(вправо).
Общее
удлинение всего стержня также равно
.