Уравнение равновесия плоской сходящейся систем сил
Сумма
проекций всех сил на ось
и
равны нулю, т.е.
,
.
Задача
3. Однородный
шар весом
(рис. 25) удерживается на гладкой наклонной
плоскости тросом. Определить натяжение
троса
и давление шара на плоскость
.
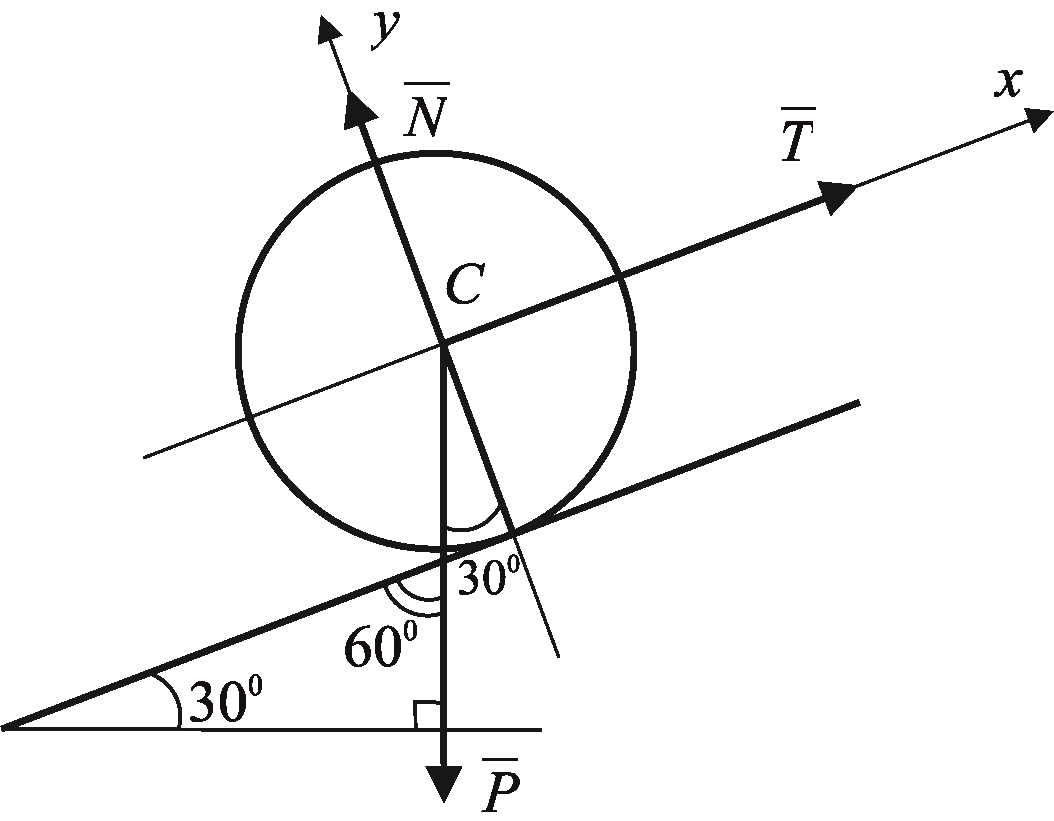
Решение.
Так как ось
можно выбрать как угодно, то ось
направим по
,
а ось
по
.
;
;
;
;
;
.
Рис. 25
Алгебраические моменты силы относительно точки
Алгебраический
момент силы
относительно центра О равен взятому с
соответствующим знаком произведению
модуля силы на ее плечо (плечо силы это
кратчайшее расстояние от линии действия
силы до данного центра), т. е.
При этом в правой системе координат, принятой в механике, момент считается положительным, когда сила стремится повернуть тело вокруг центра О против хода часовой стрелки, и отрицательным — когда по ходу часовой стрелки.
Теорема Вариньона о моменте равнодействующей
Если данная система сил имеет равнодействующую, то момент равнодействующей относительно любого центра О равен сумме моментов сил системы относительно того же центра.
Т.е.
если система сил
,
,
…
приводится к равнодействующей
,
то
.
Алгебраические моменты пары сил
Алгебраический момент пары равен взятому с соответствующим знаком произведению модуля одной из сил пары на плечо пары (плечо пары это расстояние между линиями действия сил пары):
.
Правило знаков здесь такое же, как для момента силы.
Уравнения равновесия плоской системы сил
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю.
,
,
.
Точка любая, как правило, это точка пересечения двух неизвестных реакций.
Задача
4. Жесткая
рама
(рис. 26) имеет в точке
неподвижную шарнирную опору, а в точке
- подвижную шарнирную опору на катках.
Все действующие нагрузки и размеры
показаны на рисунке.
Дано:
,
,
,
,
.
Определить реакции связей в точках , , вызываемые действующими нагрузками.
Решение.
Рассмотрим
равновесие рамы. Проведём координатные
оси
и изобразим действующие на раму силовые
факторы: силу
,
пару сил с моментом
,
натяжение троса
(
)
и реакции связей
,
,
(реакцию неподвижной шарнирной опоры
изображаем двумя её составляющими,
реакция шарнирной опоры на катках
направлена перпендикулярно опорной
плоскости).
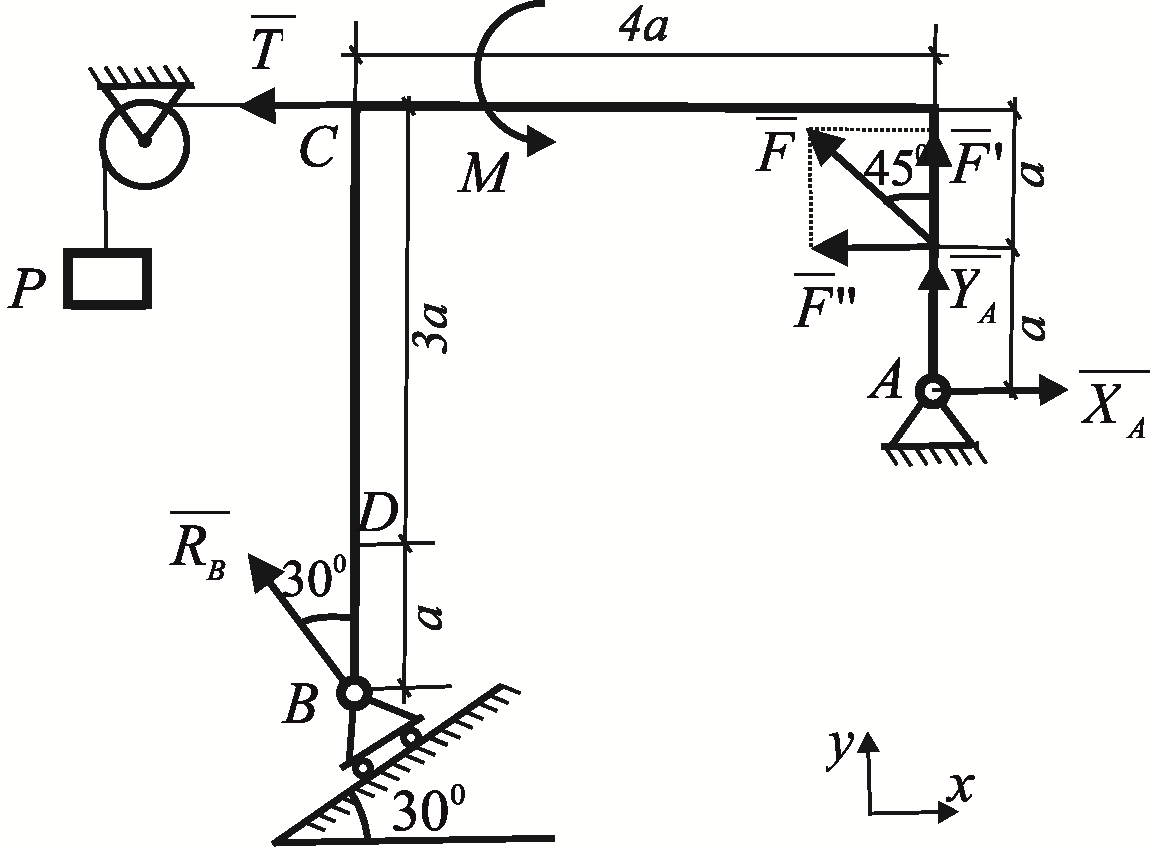
Рис. 26
Для
равновесия данной плоской системы сил
необходимо и достаточно выполнения
трёх уравнений: суммы проекций всех
сил на координатные оси
и
,
а также сумма их моментов относительно
любого центра равны нулю. В третьем
уравнении при вычислении момента силы
относительно точки
воспользуемся теоремой Вариньона, т.е.
разложим силу
на составляющие
и
(
,
)
и учтём, что
.
Получим:
:
;
:
;
:
;
Подставив
в составленные уравнения числовые
значения заданных величин, и решив эти
уравнения, определим искомые реакции:
,
,
.
Для проверки правильности ответа составляем уравнение моментов сил относительно той точки, для которой в полученном уравнении присутствовали бы ранее искомые реакции.
:
;
.
Полученный результат показывает правильность ответа.