
Элементы линейной алгебры. Глушко Е.Г., Дубровская А.П
.pdf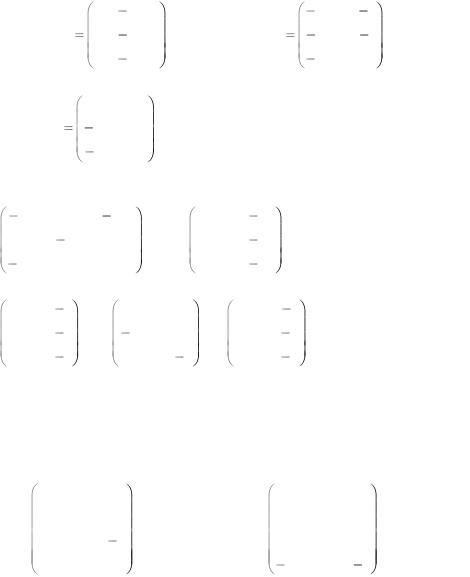
|
4 |
5 |
2 |
|
1 |
3 |
1 |
|
ж) A 5 7 3 ; |
з) A |
3 |
5 |
1 |
; |
|||
|
6 |
9 |
4 |
|
3 |
3 |
1 |
|
|
1 |
0 |
0 |
|
|
|
|
|
и) A |
4 |
4 |
0 . |
|
|
|
|
|
|
2 |
1 |
2 |
|
|
|
|
|
2. Выяснить, являются ли матрицами простой структуры следующие матрицы
|
1/ 3 4 / 3 |
2 / 3 |
|
8 |
15 |
|
36 |
|
||
а) 4 / 3 |
1/ 3 2 / 3 |
; |
б) 8 21 |
|
46 |
; |
||||
|
2 / 3 2 / 3 |
2 / 3 |
|
|
5 |
12 |
|
27 |
|
|
5 |
2 |
3 |
4 |
7 |
5 |
|
|
4 |
2 |
5 |
в) 4 |
5 |
4 ; г) |
4 5 |
0 |
; д) 6 |
4 |
9 . |
|||
6 |
4 |
4 |
1 |
9 |
4 |
|
|
5 |
3 |
7 |
3. Выяснить, какие из заданных матриц линейных операторов можно диагонализировать переходом к новому базису. Найти этот базис и соответствующую ему
диагональную форму |
|
матрицы. |
|
|
|
|
|
||||
|
1 |
1 |
2 |
3 |
|
|
0 |
1 |
0 |
0 |
|
а) |
0 |
2 |
2 |
4 |
; |
б) |
0 |
0 |
1 |
0 |
; |
|
0 |
0 |
1 |
2 |
|
|
0 |
0 |
0 |
1 |
|
|
0 |
0 |
0 |
2 |
|
|
6 1 |
7 |
1 |
|
|
101

|
1 |
1 |
1 |
|
|
|
|
|
2 |
|
1 |
2 |
|
в) 1 1 1 ; |
|
|
|
|
|
г) 5 |
|
3 3 ; |
|||
|
1 |
1 |
1 |
|
|
|
|
|
1 |
|
0 |
2 |
|
2 |
2 |
0 |
|
|
|
|
1 |
2 |
|
0 |
|
|
д) |
2 1 |
2 ; |
|
|
е) |
2 2 |
|
2 . |
|||
|
0 |
2 |
0 |
|
|
|
|
0 |
2 |
|
3 |
|
|
|
|
|
|
|
|
Ответы |
|
|
|
|
|
1. |
а) |
|
1=2, |
2=1, |
3=-1, |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
e 1=(2,1,-2), |
e 2=(1,0,-1), |
e |
3=(0,0,1); |
|
|
||||
|
б) |
|
1=5, |
2=-1, |
|
3=4; |
|
|
|
|
|
|
|
в) |
|
1= 2=1, |
3=-1, |
|
|
|
|
|
|||
|
|
|
|
|
|
|
2=(-1,0,1), |
|
|
|
|
|
|
|
|
e 1=(2,1,0), |
e |
e 3=(3,5,6); |
|
|
|||||
|
г) |
|
1=-5, 2=1, |
|
3=3, |
|
|
|
|
|
||
|
|
|
e 1=(0,0,1), |
e 2=(1,-1,0), |
e 3=(1,1,0); |
|
|
|||||
|
д) |
|
1=2, |
2= 3=1, |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
e 1=(-1,1,1), |
e 2=(1,1,0), |
e 3=(1,0,1). |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
а) |
|
e 1=(1,0,0,0), |
e 2=(1,-1,1,-1), |
|
|
|
|||||
|
|
|
e 3=(1,1,0,0), e 4=(1,0,2,-1), |
|
|
|
||||||
|
|
|
|
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
A |
0 |
1 |
0 |
0 ; |
|
|
|
|
|
|
|
|
|
0 |
0 |
2 |
0 |
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
e 1=(1,1,1,1), |
e 2=(1,-1,1,-1), |
|
|
|
|||||
|
|
|
e 3=(1,2,4,8), e 4=(1,-3,9,-27), |
|
|
|
||||||
102

д) e1
е) e1
|
1 |
0 |
0 |
0 |
|
|
A |
0 |
1 |
0 |
0 |
; |
|
0 |
0 |
2 |
0 |
|||
|
|
|||||
|
0 |
0 |
0 |
3 |
|
|
|
|
|
2=(1,0,-1), |
|
в) |
e 1=(1,1,1), |
e |
e 3=(0,1,-1), |
||
|
3 |
0 |
0 |
|
|
|
A 0 |
0 |
0 |
; |
|
|
0 |
0 |
0 |
|
|
г) Матрица не может быть диагонализирована.
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
{1, 2, 2}; A |
0 |
4 |
0 . |
||
{2,1, 2}, |
e2 |
{ 2, 2, |
1}, |
e3 |
||||
|
|
|
|
|
|
0 |
0 |
2 |
|
|
|
|
|
|
1 |
0 |
0 |
|
|
{10,15, 6}; A |
0 |
5 |
0 . |
|||
{2, 2,1}, |
e2 |
{4,12,3}, |
e3 |
|||||
|
|
|
|
|
|
0 |
0 |
2 |
5. ВЕЩЕСТВЕННОЕ ЕВКЛИДОВО ПРОСТРАНСТВО,ЕГО ПРОСТЕЙШИЕ СВОЙСТВА
До сих пор рассматривались только такие свойства линейных операторов, которые полностью определяются лишь аксиомами линейного пространства.
Это обстоятельство определяет чрезвычайно большую общность всех результатов, которые справедливы для любых
103

линейных пространств. Для получения же новых результатов необходимо несколько ограничить класс рассматриваемых пространств и тем самым получить возможность более глубокого изучения свойств линейных операторов.
Мы остановимся подробнее на важнейшем частном случае линейных пространств. Этим частным случаем вещественных линейных пространств являются, евклидовы пространства.
5.1. Определение вещественного евклидова пространства
Вещественное линейное пространство L называется
вещественным евклидовым пространством (или просто евклидовым пространством), если выполнены следующие два
требования: |
|
|
|
|
|
I. |
Имеется правило, посредством которого любым |
||||
двум элементам этого пространства |
|
и |
|
ставится в |
|
x |
y |
||||
соответствие вещественное число, называемое скалярным произведением этих элементов и обозначаемое символом
( x , y ).
II.Указанное правило подчинено следующим
четырем аксиомам:
1.( x , y )=( y , x )
(переместительное свойство или симметрия);
2.( x 1+ x 2, y )=( x 1, y )+( x 2, y )
|
(распределительное свойство); |
||||
3. |
( |
|
|
|
|
x |
, y )= |
( x |
, y ), для любого вещественного . |
||
4.( x , x )>0, если x - ненулевой элемент;
|
|
если |
|
- нулевой элемент. |
( x |
, x )=0, |
x |
||
Отметим, |
что |
при введении понятия евклидова |
||
пространства мы абстрагируемся не только от природы изучаемых объектов, но и от конкретного вида правил образования суммы элементов, произведения элемента на число и скалярного произведения элементов, важно лишь,
104

чтобы эти правила удовлетворяли восьми аксиомам линейного пространства и четырем аксиомам скалярного произведения.
Приведем примеры конкретных евклидовых пространств.
Пример 1. Рассмотрим линейное пространство R3 всех свободных векторов. Скалярное произведение любых двух векторов определим так, как это было сделано в аналитической геометрии (т.е. как произведение длин этих векторов на косинус угла между ними). В курсе аналитической геометрии была доказана справедливость для так определенного скалярного произведения аксиом 1-4.
Таким образом, пространство R3 с так определѐнным скалярным произведением является евклидовым пространством.
Пример 2. Рассмотрим бесконечномерное линейное пространство всех функций x(t), определѐнных и непрерывных на сегменте a t b.
Это пространство принято обозначать C[a,b]. Скалярное произведение двух функций x(t) и y(t) из C[a,b] определим как интеграл от произведения этих функций в пределах от a до b:
b
x(t) y(t)dt
a
Для так определѐнного скалярного произведения выполнены все четыре аксиомы определения евклидова пространства. Действительно, аксиома 1 очевидна; справедливость аксиом 2
и 3 следует |
из свойств определѐнного |
интеграла; |
|
|
b |
справедливость |
аксиомы 4 следует из того, что |
x2 (t)dt |
|
|
a |
неотрицателен, как интеграл от непрерывной неотрицательной функции и обращается в нуль лишь, когда эта функция тождественно равна нулю на сегменте [a,b].
105

Таким образом, пространство C[a,b] с так определенным
скалярным |
произведением |
является |
бесконечномерным |
||
евклидовым пространством. |
|
|
|
||
Пример 3. Пусть Ln - n-мерное линейное пространство |
|||||
упорядоченных совокупностей |
n вещественных чисел. |
Для |
|||
|
|
|
|
|
|
любых двух |
элементов |
x =(x1,x2,..,xn) и |
y =(y1,y2,..,yn) |
этого |
|
пространства определим скалярное произведение равенством:
|
|
|
( x |
, y )=x1y1+x2y2+ +xnyn . |
(5.1) |
Покажем справедливость всех четырех аксиом. Первая аксиома очевидна. Для установления справедливости аксиомы 2 и 3 воспользуемся определением операций сложения элементов и умножения их на числа. Действительно:
|
(x1,x2, |
,xn)+(y1,y2, |
,yn)=( x1+y1,x2+y2, |
,xn+yn) |
|
||
|
|
(x1,x2, ,xn)=( |
x1, x2, , |
xn) |
|
|
|
Справедливость |
аксиомы |
4 |
следует |
из |
того, |
что |
|
|
|
+xn2 всегда является неотрицательным |
|||||
( x |
, x )=x12+x22+ |
||||||
числом и обращается в нуль лишь при условии x1=x2= |
=xn=0. |
||||||
Рассматриваемое здесь евклидово пространство обозначают En.
|
|
5.2. Простейшие свойства произвольного |
|
|
|||||||||||||
|
|
|
|
евклидова пространства |
|
|
|
|
|
||||||||
|
Теорема. |
Для |
любых |
двух |
векторов |
и |
|||||||||||
|
x |
y |
|||||||||||||||
произвольного |
евклидова |
|
пространства |
|
справедливо |
||||||||||||
неравенство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
( x , |
y ) ( x , x )( y , y ), |
|
|
|
|
|
||||||
называемое неравенством Коши-Буняковского. |
|
|
|
|
|||||||||||||
|
Доказательство. Пусть |
- любое вещественное число. |
|||||||||||||||
Тогда |
|
|
- элемент этого же |
евклидова пространства, а |
|||||||||||||
x |
- y |
||||||||||||||||
следовательно, по аксиомам 1-4, |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
2 |
|
|
0 |
|
|
|||||
|
|
( x |
- y , |
x |
- y )= |
|
( x |
, x )-2 |
( x |
, y )+( y |
, y ) |
|
|
||||
Так как |
|
|
|
если |
|
|
- |
ненулевой |
|
вектор, |
то |
по |
|||||
( x , x )>0, |
|
x |
|
||||||||||||||
необходимому и достаточному условию неотрицательности квадратного трехчлена (дискриминант 0), имеем:
106

|
|
|
2 |
|
|
|
|
D=( x |
, y ) -( x |
, x )( y |
, y ) 0. |
||||
|
|
2 |
|
|
|
|
|
Отсюда следует ( x |
, y ) |
|
( x , x )( y |
, y ). |
|||
Теорема доказана.
Линейное пространство L называется нормированным, если выполнены следующие два требования:
I.Имеется правило, по которому каждому элементу
x пространства L ставится в соответствие вещественное число, называемое нормой (или длиной) указанного элемента и
обозначаемое символом x .
II. Указанное правило подчинено следующим трем аксиомам:
|
1. |
|
|
|
>0, если |
|
- ненулевой элемент; |
|
|
=0, если |
||||||||
|
|
x |
|
x |
x |
|
||||||||||||
- нулевой элемент. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2. |
|
|
|
|
|
|
|
|
|
|
, для любого |
|
L и вещественного |
||||
|
|
|
x |
|
|
|
|
|
x |
x |
||||||||
.
3.Для любых двух элементов x и y справедливо
неравенство:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
|
|
|
x |
|
|
|
y |
|
|
|
|
(неравенство треугольника или неравенство Миньковского). |
|
|||||||||||||||
Теорема. |
Всякое |
евклидово |
|
пространство является |
||||||||||||
нормированным, |
если |
|
в |
нем |
норму любого элемента |
|
||||||||||
|
x |
|||||||||||||||
определить равенством |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x |
|
|
|
(x, x) . |
|
|
|
|
|||||||
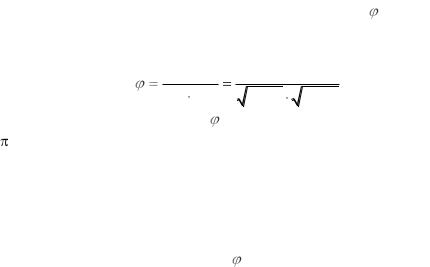
Доказательство. Аксиомы 1 и 2 для нормы вытекают из аксиом 4,1 и 3 скалярного произведения. Для доказательства аксиомы 3 воспользуемся неравенством Коши-Буняковского и аксиомами скалярного произведения. Тогда:
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x y |
|
|
|
|
(x y, x y) |
|
(x, x) 2(x, y) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x, x) 2 (x, x) |
( y, y) |
( y, y) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
||||
[ (x, x) |
|
|
( y, y)] |
|
|
|
(x, x) |
|
( y, y) |
|||||
( y, y)
xy .
107
Теорема доказана.
Теперь в любом вещественном евклидовом пространстве можно ввести понятие угла между двумя
произвольными |
векторами |
|
|
|
|
|
и |
|
этого |
пространства. По |
|||||||||||
|
|
|
|
x |
y |
||||||||||||||||
аналогии с |
векторной |
|
алгеброй, |
назовѐм |
углом |
между |
|||||||||||||||
элементами |
|
|
|
|
|
|
|
|
|
|
|
|
|
косинус которого определяется |
|||||||
x и |
y тот угол, |
||||||||||||||||||||
соотношением: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
cos |
|
|
|
(x, y) |
|
|
(x, y) |
|
. |
(5.2) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
y |
|
(x, x) ( y, y) |
|
|||
Мы предполагаем, что |
изменяется в пределах от 0 до |
||||||||||||||||||||
. Это определение угла корректно, так как дробь в правой части равенства (5.2) по модулю не превосходит единицы, что
легко следует из неравенства Коши-Буняковского. |
|
|||
Два произвольных элемента |
|
и |
|
евклидова |
x |
y |
|||
пространства E будем называть ортогональными, |
если |
|
|
|
|
произведение этих элементов ( x |
, y ) равно нулю. Очевидно, |
|
что в этом случае косинус угла |
|
|
между элементами x |
и y |
|
будет равен нулю. |
|
|
5.3. Ортонормированный базис конечномерного |
|
|
евклидова пространства. Его свойства |
|
|
В 3.4 было введено понятие базиса n - мерного линейного |
||
пространства. В линейном пространстве все базисы являлись равноправными. В евклидовом пространстве существуют специальные, особо удобные базисы, называемые ортогональными базисами. Эти базисы играют ту же роль, что и декартов прямоугольный базис в аналитической геометрии.
|
|
|
Будем говорить, что n элементов e1 |
,e2 |
,..., en |
n - мерного евклидова пространства E образуют ортонормированный базис этого пространства, если эти элементы попарно ортогональны и норма каждого из этих элементов равна единице, т.е. если:
108
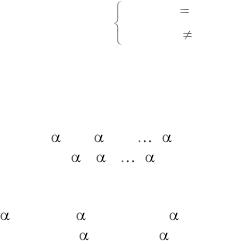
|
|
|
1 |
при i |
k, |
|
|
|
|
|
( e i, e k)= |
0 |
при i |
k . |
|
|
|
||
Это определение |
корректно, |
так как элементы |
|||||||
e1 |
,e2 |
,..., en |
|||||||
образуют один |
из |
базисов |
рассматриваемого n-мерного |
||||||
евклидова пространства En. Действительно, покажем, что эти
элементы линейно независимы, т.е., что равенство: |
|
|
|
|||||||||||||
|
|
|
|
|
|
1+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 e |
2 e 2+ + |
n e n=0 |
|
|
|
|
|
|||||
возможно, лишь когда |
|
1= |
2= |
= |
n=0. |
|
|
|
|
|
|
|||||
|
|
Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e k - любой из n элементов. Умножим последнее |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равенство скалярно на |
e k, тогда: |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1( e 1, e k)+ |
2( e 2 e k)+...+ k( e k, e k)+...+ |
|
|
|
|||||||||
|
|
|
|
|
+ |
n( e n, e k)= |
k=0. |
|
|
|
|
|
||||
|
|
Теорема. |
Во |
всяком |
n |
- |
мерном |
|
евклидовом |
|||||||
пространстве существует ортонормированный базис. |
|
|
||||||||||||||
|
|
|
Доказательство этой теоремы выходит за рамки |
|||||||||||||
нашего курса и мы его здесь не приводим. |
|
|
|
|
|
|||||||||||
|
|
Заметим только, что согласно определению размерности |
||||||||||||||
в пространстве En |
найдется n линейно независимых векторов |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f1, f2 ,..., fn . По этим векторам можно построить |
n векторов |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e1 |
,e2 |
,..., en , линейно выражающихся |
через |
f1, f2 ,..., fn |
и |
|||||||||||
образующих ортонормированный базис. |
|
|
|
|
|
|
||||||||||
|
|
Таким образом, может быть получен алгоритм |
|
|
||||||||||||
построения |
шаг |
за |
шагом |
по |
данной |
системе |
линейно |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
независимых |
элементов |
f1, |
f2 ,..., |
fn |
системы |
|
n |
попарно |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ортогональных элементов e1,e2 |
,..., en , |
норма |
каждого |
из |
||||||||||||
которых равна единице. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Указанный |
алгоритм |
обычно |
называют |
процессом |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ортогонализации линейно независимых элементов f1, f2 ,..., fn .
Подробнее с ним можно ознакомиться в [1], [5].
Конечно, в каждом n - мерном пространстве En существует много ортонормированных базисов. Примером
109

ортонoрмированного базиса может служить декартов прямоугольный базис евклидова пространства всех свободных векторов или совокупность n элементов:
|
,0), |
e 1=(1,0,0, |
|
|
,0), |
e 2=(0,1,0, |
|
... |
|
|
,1) |
e n=(0,0,0, |
евклидова пространства En всех упорядоченных совокупностей n вещественных чисел со скалярным произведением (5.1). Проверить это предлагается читателю самостоятельно.
|
|
Рассмотрим |
некоторые свойства ортонормированного |
||||||||||||
базиса: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
и |
- два произвольных элемента n - мерногo |
|||||||||||
|
|
1.Пусть x |
y |
||||||||||||
евклидова пространства |
En, |
а |
|
|
|
- |
произвольный |
||||||||
e1,e2 |
,..., en |
||||||||||||||
ортонормированный базис этого пространства. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Найдем выражение скалярного произведения ( x , |
y ) |
||||||||||||
этих |
элементов |
через |
их |
координаты относительно базиса |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e1 |
,e2 |
,..., en . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначим через x1,x2, |
,xn и y1,y2, ,yn - координаты |
||||||||||||
|
|
x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
y |
соответственно в базисе e1 |
,e2 ,..., en |
, т.е.: |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
=x1 e |
1+x2 e |
2+ +xn e n, |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
=y1 e |
1+y2 e |
2+ +yn e n. |
|
|
|
||||
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
2+ |
|
|
|
|
( x |
, y )=(x1 e 1+x2 e 2+ |
+xn e n)(y1 e |
1+y2 e |
+yn e n)= |
|
||||||||
|
|
|
|
n |
|
n |
|
|
|
n |
n |
|
|
|
|
|
|
|
= |
|
xiei |
, |
yk ek |
|
|
xi yk (ei |
, ek ) = |
|
|||
|
|
|
|
i 1 |
|
k |
1 |
|
|
i 1 |
k 1 |
|
|
|
|
=x1y1+x2y2+ +xnyn,
так как все слагаемые, содержащие скалярные произведения
|
|
|
|
( e i, e k)=0 при i |
k, и ( e i, e k)=1, при i=k. |
||
110
