Учебное пособие 1991

уравнением.

Раскрывая определитель, получаем многочлен n-ой

степени относительно :

n+p1 n-1+...+pn-1 +pn=0.

Корни характеристического уравнения и являются собственными значениями линейного оператора. Для нахождения собственных векторов по полученным собственным значениям необходимо решить однородную систему (4.3).

Пример 1. Найти собственные значения и собственные

векторы линейного оператора A , заданного в некотором базисе матрицей:

1 3 3

1 4 8

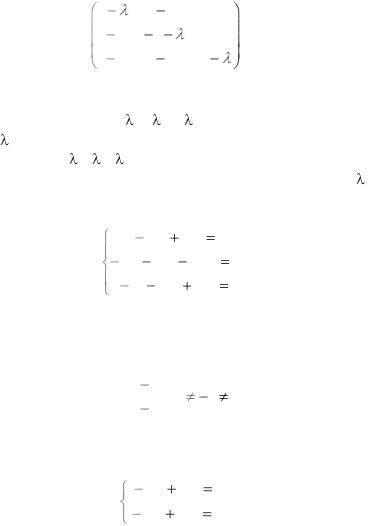
Решение. Составим характеристическое уравнение:

91

Таким образом, 1= 2= 3=1 .

Найдем теперь собственные векторы, подставив число =1 в систему (4.3):

3x2 3x3 0 , 2x1 7x2 13x3 0 ,

x1 4x2 7x3 0 .

Определитель системы равен нулю, следовательно, ранг матрицы системы меньше трех, один из миноров второго порядка отличен от нуля:

значит, ранг системы равен двум. Составим укороченную систему уравнений, эквивалентную заданной, определитель которой совпадает с базисным минором M2.

3x2 3x3 0 ,

4x2 7x3 x1 .

Пусть x1=1, тогда, решив систему, имеем x2=x3=1/3. Таким образом, для данного линейного оператора, имеющего три равных собственных значения, существует только один

собственный вектор: x ={1,1/3,1/3}.

92

Пример 2. Найти собственные значения и собственные векторы оператора A , заданного в некотором базисе матрицей:

Решение. Составим характеристическое уравнение и

При 1=1 получим следующую систему для нахождения координат собственного вектора:

3x1 5x3 0 ,

7x1 3x2 9x3 0 , 3x1 5x3 0 .

Отбрасывая третье уравнение, получаем:

3x1 5x3 0 ,

7x1 3x2 9x3 0 .

Пусть x3=1, тогда x1=-5/3, x2=62/9.

При 2=9 получим:

5x1 5x3 0 ,

7x1 11x2 9x3 0 , 3x1 3x3 0 .

93

В данной системе первое и третье уравнения эквивалентны, поэтому координаты соответствующего собственного вектора определим как решения системы:

x1 x3 0 ,

7x1 11x2 9x3 0 .

Пусть x3=1, тогда x1=1,x2=16/11. При 3=-2 получим

6x1 5x2 0 ,

7x1 9x2 0 ,

3x1 8x2 0 .

или x1=0,x3=0,x2=1.

Итак, мы получили следующие собственные векторы:

Пример 3. Найти собственные значения и собственные

векторы линейного оператора A , заданного в некотором базисе матрицей:

Решение. Найдем собственные значения матрицы A:

Отсюда 1=1 - корень характеристического уравнения второй

94

Придавая неизвестным x2 и x3 различные значения, например x'2=1, x'3=0 и x"3=1, x"2=0, получим два линейно независимых вектора:

отвечающих собственному значению 1=1.

Для 2=2 система уравнений (4.3) примет вид: x2 x3 0 ,

x1 2x2 x3 0 , x1 x2 0 .

Заметим, что второе уравнение является суммой первого и третьего и его можно отбросить. Получается система:

или x3=x2, x1=x2. Пусть x2=1, тогда x3=1, x1=1 и

Приведенные выше примеры показывают, что не всегда линейный оператор имеет столько же собственных векторов, какова размерность пространства.

Так как определитель матрицы оператора не зависит от выбора базиса, то и собственные значения также не зависят от выбора базиса.

Теорема. Если все собственные значения матрицы A линейного оператора различны, то соответствующие

собственные векторы.

95

Предположим противное: система собственных

собственный вектор. Полученное противоречие доказывает теорему.

4.7. Приведение матрицы оператора к диагональному виду

Пусть оператор A действует из линейного пространства L размерности n в это же пространство. Предположим, что у

96

Таким образом, матрица линейного оператора в базисе из собственных векторов имеет диагональный вид, причем на

Итак, 1=1, 2=-2, 3=4.

Найдем теперь базис из собственных векторов, в котором матрица A имеет диагональный вид.

Для 1=1 имеем:

97

3=4.

Матрицей перехода от старого базиса B к базису из собственных векторов B’ будет матрица:

Следовательно, используя формулу для нахождения матрицы оператора при переходу к новому базису, имеем:

1 0 0 A 0 2 0 .

0 0 4

Выясним, в каком случае существует базис из собственных векторов.

Оказывается, что можно найти базис из собственных векторов не только в случае различных собственных значений, но и в случае кратных собственных значений, если каждому собственному значению соответствует столько линейно независимых собственных векторов, какова его кратность. Таким образом, матрица может быть приведена к диагональному виду, если существует базис из собственных векторов этой матрицы.

Определение. Матрицы, приводимые к диагональному виду, называются матрицами простой структуры.

98

В квантовой механике важную роль играют матрицы, обладающие свойством коммутативности. Зная собственные значения и собственные векторы матриц, можно, пользуясь следующей теоремой, ответить на вопрос коммутируемости матриц.

Теорема. Пусть собственные значения матриц A и B простые. Матрицы А и В коммутируют тогда и только тогда, когда они имеют одинаковые собственные векторы.

Доказательство. Пусть матрицы A и B коммутируют.

собственным вектором матрицы А, отвечающим тому же собственному значению . Так как собственное значение

матрицы В.

Обратно, если А и В имеют одинаковые собственные векторы, то в одном и том же базисе они приводятся к диагональному виду и, очевидно, коммутируют.

Обсудим также некоторые вопросы приближенного нахождения собственных значений и собственных векторов матриц операторов.

В ряде прикладных задач требуется приближенное нахождение всех собственных значений некоторых матриц, а иногда и всех собственных векторов. В такой постановке в вычислительной математике задачу называют полной проблемой собственных значений.

Довольно часто определению подлежат не все собственные значения и не все собственные векторы, а, например, максимальное или минимальное по модулю собственное значение, или же значение, наиболее близко

99

расположенное к заданному числу. Такие задачи являются примерами частичных проблем собственных значений.

Ранее численные методы решения проблемы собственных значений сводились, в основном, к решению характеристического уравнения. Однако, такой подход становится неудовлетворительным для матриц большого размера. Кроме того, хотя задача нахождения собственных значений матриц и корней характеристического уравнения формально эквивалентны, они имеют разную обусловленность, т.к. корни многочлена высокой степени чрезвычайно чувствительны к погрешностям в коэффициентах. Поэтому сейчас наиболее распространены приближенные методы решения проблемы собственных значений, не использующие вычисление характеристического многочлена. В качестве примера таких методов далее будет рассмотрен степенной метод.

Упражнения

1. Найти собственные значения и собственные векторы матрицы А линейного оператора, если:

100