Учебное пособие 1991

Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

a 1=(2,3,5),

a 2=(0,1,2), a 3=(1,0,0)

оператором

преобразуются соответственно

b 1=(1,1,1),

b 2=(1,1,-1),

b 3=(2,1,2).

Найти матрицу этого

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

3.61 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 159 10 11 12 13 14 15 > Следующая >>>

			x2+ x3)=
	A (	x )=( x2+ x3,2 x1+ x2,3 x1-	x2+ x3)=
		= (x2+x3,2x1+x2,3x1-x2+x3)=
		= (x2+x3,2x1+x2,3x1-x2+x3)=	A x ;

A ( x	+ y )=(x2+y2+x3+y3,2x1+2y1+x3+y3,3x1+3y1-x2-y2+x3+y3)=

=(x2+x3, 2x1+x2, 3x1-x2+x3)+(y2+y3, 2y1+y2, 3y1-y2+y3)=

=A x + A y .

Следовательно,										,
Следовательно,				A - линейный оператор. Далее,			Ae1	2e2	3e3	,

Ae2	e1	e3	, Ae3	e1	e3	e3 .
			0	1	1
Значит, A			2	0	1 .

31 1

3.В пространстве R3 заданы два линейных оператора A

и B . Найти матрицу С линейного оператора C									AB	BA и его

явный вид в каноническом базисе						3:
			=(2x2-2x1+3x2+2x3,4x1-x2+5x3),
		A x	=(2x2-2x1+3x2+2x3,4x1-x2+5x3),

		B x =(-3x1+x3,2x2+x3,-x2+3x3).
Решение. Так как,
							0 , 2 , 5 и
Ae1	0 , 2 , 4 , Ae2			2 , 3 , 1 , Ae3			0 , 2 , 5 и
							1, 1, 3 , то
Be1	3 , 0 , 0 , Be2			0 , 2 , 1 , Be3			1, 1, 3 , то
			0	2	0	3	0	1
		A	2	3	2 , B	0	2	1 .
			4	1	5	0	1	3
		0	4	2		3	0	1
Далее,	AB	6	4	7	, BA	0	2	1 .
		12	7	18		0	1	3
Поэтому

4 11 3 C AB BA 6 1 2 .

26 1 5

По определению матрицы линейного оператора в каноническом базисе R3 ее столбцы являются наборами компонент образов базисных векторов, т.е.

	( 4,6,			11,	1,		3 ,	26 , 6 .
Ce1	( 4,6,		26) , Ce2	11,	1,	1 ,Ce3	3 ,	26 , 6 .
Отсюда находим:
				x2e2	x3e3
	Cx	C x1e1		x2e2	x3e3	x1Ce1	x2Ce2		x3Ce3

=(-4x1+11x2-3x3,6x1-x2-2x3,-26x1-x2+5x3).

4.5 Геометрический смысл определителя матрицы оператора в пространствах R3 и R2.

1. Изменение объѐма. Рассмотрим пространство R3.

Пусть оператор A - невырожденный.			Это означает,				что он

любые три некомпланарных вектора ( e			1, e	2, e	3) переводит в
три	некомпланарных	вектора
три	некомпланарных	вектора		( A e		1, A e	2, A e 3).

Параллелепипед, построенный на векторах e1 ,					e2	, e3 , оператор

A в силу линейности преобразует в параллелепипед, построенный на их образах. Найдем соотношения между объѐмами этих параллелепипедов.

Как известно, ориентированный объѐм параллелепипеда, построенного на трех векторах, равен их смешанному произведению. Поэтому

V(1) =

e , V(2) = A

A e 2

A e 3

Выражая

A e

1, A

e 2,

e 3 по формулам:

A e

1 = a11 e

1+a21 e

2+a31 e 3

A e

2 = a12 e

1+a22 e

2+a32 e 3

A e

3 = a13 e

1+a23 e

2+a33 e 3

получаем

V(2)=(a11a22a33 + a12a23a31 + a13a21a32 - a13a23a31 -

-a12a21a33 - a11a23a32)( e1 e2 e3 )

или

V(2)=detA V(1),

где А - матрица оператора A . Отметим: что если detA>0, то оба параллелепипеда одинаково ориентированы, если detA<0, то ориентация их разная.

Итак, определитель матрицы оператора равен отношению ориентированных объемов соответствующих параллелепипедов в пространствах образов и прообразов. Иначе, он является коэффициентом искажения объѐма.

	2.Изменение площади.						Пусть		оператор	A	переводит

неколлинеарные				векторы		e 1, e2		пространства		R2	в векторы

A e	1, A e 2. Возьмѐм единичный вектор e 3, перпендикулярный

плоскости векторов e 1,					e 2. Введѐм вспомогательный оператор
A 1, (действующий в пространстве R3) такой, что :

					A		=
					A	1 e 1	=	A e 1,
					A		=
					A	1 e 2	=	A e 2,

					A 1 e		3 = e 3.
	Тогда ориентированные объѐмы V(1) и V(2) численно
равны площадям параллелограммов S(1) и S(2), построенных на

векторах		e	1, e 2	и их образах. С					учетом результата п.1,
получаем S(2)=S(1)detA1.
	Нетрудно			видеть,			что		detA1=detA.		Значит
S(2)=detA S(1),т.е.				detA	является			коэффициентом			искажения

площади.

Упражнения

1. Установить, какие из заданных отображений пространства

R3 в себя являются						линейными операторами; выписать их

матрицы в прямоугольном базисе B=( i , j , k ):
а)		=		,	-	фиксированное число;
	A x		x
б)		=			,		- фиксированное число;
	A x		x	+ a		и a
в)							- заданный единичный
	A x	=( x , e ) e				, где e

вектор, выяснить геометрический смысл этого отображения;

г)					- фиксированный вектор.
г)	A x	=[ a	, x	], a	- фиксированный вектор.
д)						- фиксированный вектор.
д)	A x	=( a	, x ) x ,		a	- фиксированный вектор.
2.		Установить,				какие из заданных отображений

пространства арифметических векторов R3 в себя являются линейными операторами; выписать их матрицы в каноническом базисе:

а) A x =(x1,x2+1,x3+2);

б) A x =(0,x2-x3,0);

в) A x =(x1+2x2+2x3,-3x2+x3,2x1+3x3);

г) A x =(3x1+x2,x1-2x2-x3,3x2+2x3).

3.Показать, что ортогональное проектирование

трехмерного пространства на ось 0X есть линейный оператор.


Найти его матрицу в базисе B=( i , j , k ).
4. В пространстве R3 заданы два линейных оператора A

и B . Найти матрицу С линейного оператора			C	AB	BA и его

явный вид в каноническом базисе R3:
а)		=(7x1+4x3,4x2-9x3,3x1+x2);
а)	A x	=(7x1+4x3,4x2-9x3,3x1+x2);
		=(x2-6x3,3x1+7x3,x1+x2-x3);
	B x	=(x2-6x3,3x1+7x3,x1+x2-x3);

б) A x =(2x1-x2+5x3,x1+4x2-x3,3x1-5x2+2x3);

x =(x +4x +3x ,2x +x ,3x -x );

B 1 2 3 1 3 2 3

в) A x =(3x1+x2-2x3,3x1-2x2+4x3,-3x1+5x2-x3);

		=(2x1+x2,x1+x2+2x3,-x1+2x2+x3);
	B x
г)		=(3x1+x2+x3,2x1+x2+2x3,x1+2x2+3x3);
	A x
		=(x1+x2-x3,2x1-x2+x3,x1+x2).
	B x

оператора в том же базисе, в котором указаны координаты

векторов

и b .

В L4

задан линейный оператор A , матрица которого в

некотором базисе B=( e

1, e

2, e

3, e 4) равна:

2 .

Найти матрицу этого оператора в базисах:

4);

а)

B'=( e

1, e

3, e

2, e

б)

B'=( e

1, e

1+ e

2, e

1+ e 2+ e

3, e 1+ e 2+ e

3+ e 4).

В L3

задан линейный оператор A , матрица которого в

некотором базисе B=( e

1, e

2, e 3) равна:

8 .

Найти матрицу этого оператора в базисе

B': e1

=2 e 1+3 e 2+ e 3,

e2 =3 e 1+4 e

2+ e

3, e3

= e

1+2 e 2+2 e 3.

8. В L3 заданы два базиса:

B': e1 =8 e

1-6 e 2+7 e 3,

e2 =-16 e

1+7 e

2-13 e

3, e3

=9 e

1-3 e

2+7 e 3,

B'': e1

= e 1-2 e

2+ e 3, e2

=3 e

1- e

2+2 e 3,

=2 e

1+ e

2+2 e 3 .

Найти матрицу оператора A в базисе B'', если его матрица в

базисе B' имеет вид:

20 .

9.В пространстве L2

оператор

A в базисе B': e

1= e 1+2 e 2,

имеет матрицу A

. Оператор

в базисе

e2 =2 e

1+3 e 2

B'':

матрицу

=3 e 1+ e

2, e2

=4 e 1+2 e 2 имеет

Найти матрицу оператора A + B

в базисе B''.

10. В пространстве L2 оператор A в базисе B':

матрицу A

2e2

имеет

Оператор B в базисе B'': e1

=6 e 1-7 e 2,

=-5 e 1+6 e 2

матрицу B

7 .

Найти

матрицу оператора

том

базисе, в котором даны координаты всех векторов.

11.

пространстве

задан линейный

оператор

дифференцирования D

. Найти матрицу этого оператора в

базисе 1,t,t2,…,tn.

12. В пространстве функций, дифференцируемых на всей

оси, заданы оператор дифференцирования

и оператор

A умножения на функцию e . Проверить равенство D A -

A D =	A .

13.Установить, какие из заданных линейных операторов

вR3 являются невырожденными, и найти явный вид обратных операторов:

	а)		=(x1-x2+x3,x3,x2)
	а)	A x	=(x1-x2+x3,x3,x2)
	б)		=(x2+2x3,-x2,2x2-x3).
	б)	A x	=(x2+2x3,-x2,2x2-x3).
						Ответы
								0	0
1.	а)		является;			A	0		0	;б)	не является;
							0	0
	в)		является		оператором			проектирования на ось,
							cos		cos
заданную вектором e , если						e	cos	i	cos	j	cos k ,
			cos2		cos		cos		cos	cos
то		A	cos	cos		cos2			cos	cos	;
			cos	cos	cos		cos		cos2

	г)		является, если			a	a1i		a2 j	a3k ,
			0	a3	a2
то	A		a3	0	a1	;
			a2	a1	0

д) не является.

	0	0	0
2.	а) не является; б) является; A 0	1	1
	0	0	0

			1	2	2		3	1	0
в) является;			A 0	3	1	; г)является; A	1	2	1 ;
			2	0	3		0	3	2
	1	0	0
3.	0	0	0 .
	0	0	0

		22			13	37
4.	а)	C	39		16	25 ,
			1		0	6
		=(22x1+13x2-37x3,-39x1-16x2+25x3,-x1-6x3);
	Cx	=(22x1+13x2-37x3,-39x1-16x2+25x3,-x1-6x3);
			15		23	7
	б)	C	2		8	4 ,
			7		1	7

	Cx =(-15x1+23x2-7x3,2x1+8x2-4x3,-7x1+x2+7x3);
	в)
	в)	C=0, cx		= 0 ;
		2		3	2
	г)	C 1		0	4	,
		5		0	2

Cx =(2x1+3x2-2x3,x1-4x3,5x1-2x3).

2 11 6

5. 1 7 4 .

2 1 0

		1	0	2	1			2	0	1	0
6.а)	A	2	3	5	1	;	б) A	1	4 8 7 .
		3	1	0	2			1	4	6	4
		1	1	2	3			1	3	4	7

	1	0	0		1	2	2	44	44
	0	2	0	. 8. A"	3	1	2 . 9.	44	44
7.	0	2	0	. 8. A"	3	1	2 . 9.	29.5	25 .
	0	0	3		2	3	1

10.109 93 .

34 29

	0	1
		0	2		0
11.			0	3	.
11.					.

		0			0 n 1
					0
13.	а)		1
13.	а)		A		A ;
	б)		оператор не имеет обратного.

4.6. Cобственные значения и собственные векторы линейного оператора

Пусть	A	- линейный		оператор, действующий из

конечномерного линейного пространства L в это же
пространство.
Ненулевой		вектор		L называется	собственным
Ненулевой		вектор	x	L называется	собственным
вектором	линейного		оператора A , если		справедливо

равенство:

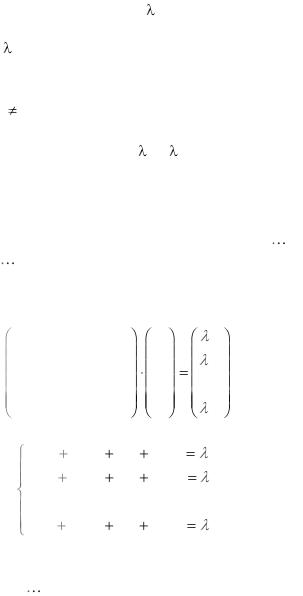
	=		(4.2)
A x		x .

Скаляр называется собственным значением линейного

оператора A , соответствующим собственному вектору x .

Пусть x - некоторый собcтвенный вектор. Покажем, что

вектор k x , k 0 также является собственным вектором, отвечающим тому же собственному значению. Действительно,

A (k x )=k A

Выберем в n-мерном

базис, например e 1, e 2,..,

	=k		=
x	=k	x	=	(k x ).

пространстве Ln какой-нибудь

e n. В этом базисе линейный

оператор	A определяется матрицей n-го порядка,				столбцами


которой являются координаты векторов A e 1,				A e	2, , A e n в

базисе e	1, e 2,	, e n.
Пусть вектор			x имеет координаты x1,x2,..,xn		в этом же

базисе. Тогда соотношение (4.2) в матричной форме будет представлено в виде:

a11	a12	a1n		x1	x1
a21	a22	a2n		x2	x2	,
						,

an1	an 2	ann		xn	xn
или
a11 x1		a12 x2	a1n xn		x1
a21 x1		a22 x2	a2n xn		x2

an1x1		an 2 x2	ann xn		xn

Перенесѐм правые части влево и получим следующую однородную систему из n уравнений относительно неизвестных x1,x2, ,xn:

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 159 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20223.57 Mб8Учебное пособие 1987.pdf
#
30.04.20223.59 Mб1Учебное пособие 1988.pdf
#
30.04.20223.6 Mб6Учебное пособие 1989.pdf
#
30.04.2022325.34 Кб2Учебное пособие 199.pdf
#
30.04.20223.6 Mб2Учебное пособие 1990.pdf
#
30.04.20223.61 Mб1Учебное пособие 1991.pdf
#
30.04.20223.61 Mб3Учебное пособие 1992.pdf
#
30.04.20223.63 Mб1Учебное пособие 1993.pdf
#
30.04.20223.66 Mб5Учебное пособие 1994.pdf
#
30.04.20223.67 Mб7Учебное пособие 1995.pdf
#
30.04.20223.67 Mб3Учебное пособие 1996.pdf