
Учебное пособие 1991
.pdf
б) Найти матрицу оператора |
|
** |
в собственном |
A |
|
||
ортонормированном базисе. |
|
|
|
4.При каких условиях диагональная матрица будет ортогональной?
5.Найти ортонормированный базис из собственных векторов и матрицу в этом базисе для линейного оператора, заданного в некотором ортонормированном базисе матрицей A (искомый базис определѐн неоднозначно):
|
|
11 |
2 |
8 |
|
|
|
|
|
17 |
8 |
4 |
|
1) |
A |
2 |
2 |
10 |
|
; |
2) |
|
A |
|
8 |
17 |
4 . |
|
|
8 |
10 |
5 |
|
|
|
|
|
4 |
4 |
11 |
|
|
|
|
|
|
|
|
Ответы |
|
|
|
|
||
|
|
|
3 |
6 |
|
|
|
83 |
59 |
|
45 |
|
|
1. |
1) |
|
; |
2) |
107 |
83 |
|
67 |
; |
|
|||
|
1 |
3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
14 |
10 |
|
3 |
|
|
|
|
|
14 |
8 |
|
|
|
8 |
|
|
|
|
|
|
3) |
|
11 |
2 |
6 |
|
6 . |
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||
|
|
|
11 |
6 |
|
2 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
3 2 |
|
2 |
|
12 |
|
|
1 |
1 |
1 |
2. |
1) |
D= 12 |
|
0 |
|
12 ,D*= 0 0 0 ; |
|||||||
|
|
|
12 |
|
2 |
|
3 2 |
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
0 |
1 |
|
0 |
|
|
|
0 |
2 |
3 |
0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
|
2) |
D= 0 0 3 , |
|
D*= 1 0 |
12 . |
||||||||
|
|
|
0 |
0 |
|
0 |
|
|
|
0 |
4 |
|
0 |
|
|
|
|
|
|
|
|
|
|
3 |
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
а) |
e 1=(2/3,2/3,1/3); |
e 2=(2/3,-1/3,-2/3); |
||||||||||
121

e 3=(1/3,-2/3,2/3);
|
|
|
|
9 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
б) |
0 |
18 |
|
0 . |
|
|
|
|
|
|
|||||||
|
|
|
|
0 |
0 |
|
9 |
|
|
|
|
|
|
|
|
|
||
4. |
Диагональные элементы равны 1. |
|
|
|
||||||||||||||
|
2 3 |
|
|
|
13 |
|
|
|
|
|
2 3 |
|
|
9 |
0 |
0 |
||
2 |
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|||
5.1) e1 |
|
|
, e2 |
|
3 |
, |
|
|
e3 |
, D= |
0 |
9 |
0 ; |
|||||
3 |
|
|
|
|
|
3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
13 |
|
|
|
2 3 |
|
|
|
|
|
2 3 |
|
|
0 |
0 |
18 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
2 3 |
|
|
|
|
|
|
2 |
|
|
|
|
18 |
|
|
|
|
|
9 |
0 |
0 |
||||
1 |
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|||
2) e1 |
|
|
, e2 |
|
|
|
|
|
|
, e3 |
|
,D= |
0 |
9 |
0 . |
|||
2 |
|
|
|
|
18 |
|
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
27 |
|||||
|
0 |
|
|
|
|
4 |
|
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
7. КВАДРАТИЧНЫЕ ФОРМЫ |
|
|||||||||||||
|
Ранее нам часто приходилось рассматривать |
|||||||||||||||||
однородный |
многочлен первой степени |
от |
n |
переменных |
||||||||||||||
a1x1+a2x2+ +anxn, который называется линейной формой этих переменных.
Обобщением линейной формы n переменных являются так называемые квадратичные формы, которые тесно связаны с изучением кривых и поверхностей второго порядка в n мерном евклидовом пространстве.
Общее уравнение таких кривых и поверхностей в декартовых координатах содержит сумму квадратичной формы, линейной формы и некоторой постоянной, причѐм преобразованиям переменных и связанным с ними преобразованиям квадратичной и линейной формы
122

соответствуют преобразования поворота и параллельного переноса системы координат, что используется для исследования кривых и поверхностей второго порядка и приведения их уравнений к каноническому (простейшему) виду.
7.1. Квадратичная форма и еѐ матричная запись
Квадратичной формой переменных x1,x2, ,xn
называется однородный многочлен второй степени относительно этих переменных, т.е.:
n |
n |
L(x1, x2 ,.., xn ) |
aij xi x j , где aij=aji. |
i 1 |
j 1 |
Матрица A={aij} называется матрицей квадратичной формы L(x1,x2, ,xn) в заданном базисе. Она является симметричной.
Например, квадратичная форма при n=2 принимает вид
L(x1,x2)=a11x12+2a12x1x2+a22x22.
Действительно, по определению, имеем
2 |
2 |
|
= a11x12+a12x1x2+a21x2x1+a22x22 = |
|||
L(x1,x2)= |
a x x |
j |
||||
|
ij i |
|
|
|
|
|
i 1 |
j 1 |
|
|
|
|
|
|
|
|
= a11x12+2a12x1x2+a22x22. |
|
||
Если ввести матрицы A= a11 |
a12 |
, X= x1 |
, то |
|||
|
|
|
a21 |
a22 |
x2 |
|
L(x1,x2)=x1(a11x1+a12x2)+x2(a21x1+a22x1)=XTAX.
Таким образом, квадратичная форма при n=2 представлена в виде произведения матриц:
L(x1,x2)=XTAX.
Покажем, что эта формула справедлива и в общем случае. Действительно, введем матрицу из коэффициентов формы:
123
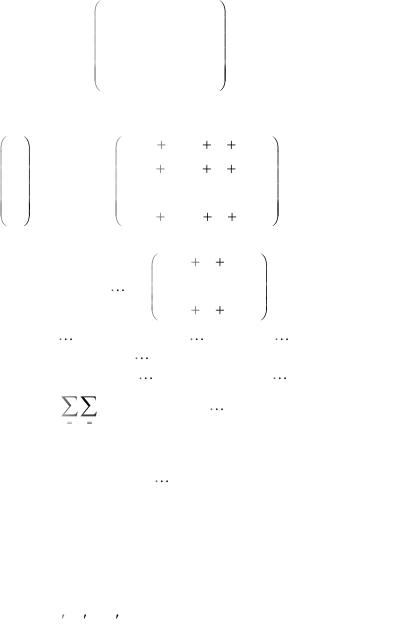
|
|
a11 |
a12 |
a1n |
|
|
|
A= |
a21 |
a22 |
a2 n |
. |
|
||
|
|
|
|
|
|||
|
|
|
|
||||
|
|
an1 |
an2 ann |
|
|
||
Очевидно, что если дана квадратичная форма, то матрица A |
|||||||
(симметрическая) известна. |
|
|
|
|
|
||
x1 |
|
|
a11 x1 |
a12 x2 ... |
a1n xn |
|
|
Пусть X= x2 , тогда AX= a21 x1 |
a22 x2 ... |
a2n xn |
|
||||
|
|
|
|
|
|
|
|
xn |
|
|
an1 x1 |
an 2 x2 ... |
ann xn |
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
a11x1 ... |
a1n xn |
|
|
XTAX=(x1 x2 |
xn) |
|
|
= |
|
||
|
|
|
|
an1x1 ... |
ann xn |
|
|
=(a11x1+ +a1nxn)x1+(a21x1+ +a2nxn)x2+ + |
|
||||||
|
+(an1x1+ +annxn)xn = |
|
|
||||
=a11x12+2a12x1x2+2a13x1x3+ +2a1nx1xn+a22x22+ +annxn2= |
|||||||
n |
n |
|
|
|
|
|
|
= |
|
aij x1x2 = L(x1,x2, ,xn). |
|
||||
i 1 |
j 1 |
|
|
|
|
|
|
Итак, для любой квадратичной формы в заданном |
|||||||
базисе имеет место формула: |
|
|
|
|
|||
|
|
L(x1,x2, |
,xn)=XTAX. |
(7.1) |
|||
Мы будем рассматривать только вещественные квадратичные формы (aij - вещественные числа).
7.2. Преобразование квадратичной формы
Очевидно, что при изменении базиса будет меняться и матрица квадратичной формы. Пусть в Еn заданы два базиса:
|
|
|
|
|
|
|
B: e1 |
, e2 |
,..., en |
и B': e1 |
,e2 |
,...en |
. Тогда для квадратичной формы в |
124

базисе В имеет место формула:
L(x1,x2, ,xn)=XTAX.
Найдем вид квадратичной формы в базисе В'. Обозначим через С матрицу перехода от базиса В к В'. Тогда из (3.7) имеем:
X=CX', XT=(CX')T=(X')TCT.
Используя (7.1) получаем:
L(x'1, x'2, ,x'n)=(X')T CTACX'=(X')TА'X',
где А'=CTAC.
Таким образом, в новом базисе квадратичная форма примет вид:
L(x'1,x'2, ,x'n)=(X')TA'X'.
7.3 Приведение квадратичной формы
кканоническому виду (сумме квадратов)
Выберем такой новый базис, чтобы матрица A' стала в нѐм диагональной. Это возможно, так как матрица A - вещественная и симметрическая.
Известно, что в этом случае базис должен быть образован из собственных векторов матрицы A, а матрица A' в этом базисе имеет вид:
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
0 |
2 |
0 |
( |
i ij ) , |
|
A'= |
|
|
|
||
|
|
|
|||
0 |
0 |
|
n |
|
|
|
|
|
|
|
|
где i - собственные значения (вещественные) матрицы A, а
|
0,i |
j |
ij= |
1,i |
j . |
Тогда преобразованная квадратичная форма принимает вид:
n |
n |
L(x'1,x'2, ,x'n)= |
i ij xi x j , |
i 1 |
j 1 |
или
125

|
n |
L(x'1,x'2, ,x'n)= |
x 2 . |
|
i i |
i |
1 |
Здесь число отличных от нуля коэффициентов  матрицы A.
матрицы A.
Итак, для того, чтобы квадратичную форму привести к каноническому виду, нужно выбрать базис, определяемый собственными векторами симметрической матрицы A.
При этом квадратичная форма приобретает вид:
L(x1,x2, ,xn)= 1x12+ 2x22+ + nxn2.
Пример. Привести к каноническому виду форму:
L(x1,x2,x3)=x12-2x22+x32+4x1x2-8x1x3-4x2x3
Решение. Составим матрицу A квадратичной формы:
|
|
|
1 |
2 |
4 |
|
|
|
|
A= |
2 |
2 |
2 . |
|
|
|
|
|
4 |
2 |
1 |
|
|
Еѐ характеристическое уравнение: |
|
||||||
|
2 |
|
4 |
|
|
|
|
|
1 |
|
|
|
|
||
|
2 |
2 |
|
2 |
|
0 или ( |
-6)( +3)2=0. |
|
4 |
2 |
1 |
|
|
|
|
Следовательно, |
1=6, 2=-3, |
3=-3. |
|
||||
Найдем |
базис из |
собственных |
векторов матрицы A. |
||||
Пусть = 1, тогда для нахождения координат собственного вектора имеем следующую систему уравнений:
5x1 |
2x2 |
4x3 |
0 , |
2x1 |
8x2 |
2x3 0 . |
|
Предположим, x3=1, тогда |
|
|
|
5x1 2x2 4 , |
x1 |
1, |
|
x1 4x2 |
1, |
x2 |
0.5 . |
и собственному значению |
1=6 отвечает собственный вектор |
||
|
|
|
|
e 1={-1,-0.5,1}. |
|
|
|
126

|
|
Пусть |
= 2, тогда получим следующее уравнение для |
|||||
нахождения координат собственных векторов: |
|
|
||||||
|
|
|
|
|
2x1+x2-2x3=0, |
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, e2 |
={1,0,1}, e3 ={-1,4,1}. В полученном базисе |
|||||||
|
|
|
|
|
|
|
|
|
e1 |
, e2 |
, e3 |
канонический вид квадратичной формы будет: |
|
||||
|
|
|
|
|
L(x1,x2,x3)=6x'12-3x'22-3x'32. |
|
|
|
|
|
Квадратичная форма L(x1,x2, ,xn), определѐнная в |
||||||
вещественном линейном пространстве En, |
называется |
|||||||
положительно |
(отрицательно) |
определѐнной, |
если |
|||||
L(x1,x2, |
,xn)>0 (L(x1,x2, ,xn)<0) при всех x 0, x |
En. |
|
|||||
|
|
Ясно, |
что |
положительно определенная |
квадратичная |
|||
форма приводится к сумме квадратов с положительными коэффициентами. Важным критерием положительной определѐнности формы является следующая
теорема (критерий Сильвестра). Для того, чтобы квадратичная форма L(x1, ,xn) была положительно определѐнной, необходимо и достаточно, чтобы были положительны все ―угловые миноры‖ матрицы A, т.е. чтобы имели место неравенства:
|
a11 |
a12 |
|
|
a11 |
a12 |
a13 |
|
|
|
|
|
|
||||||
1= a11 >0, 2= |
|
>0, 3= |
a |
a |
a |
>0, , |
n>0 |
||
|
a21 |
a22 |
|
|
21 |
22 |
23 |
|
|
|
|
|
a31 |
a32 |
a33 |
|
|
||
|
|
|
|
|
|
|
Сформулируем условия отрицательной определѐнности квадратичной формы. Для того, чтобы квадратичная форма была отрицательно определѐнной, необходимо и достаточно чтобы квадратичная форма - L(x1, ,xn) была положительно определѐнной, т.е. чтобы знаки угловых миноров матрицы A чередовались, начиная со знака минус:
|
|
a11 |
a12 |
|
|
n |
1=a11<0; |
2= |
a |
a |
>0; |
3<0, , (-1) |
n>0 |
|
|
21 |
22 |
|
|
|
Пример. Проверить, что квадратичная форма
L(x1,x2,x3)=12x1x2-12x1x3+6x2x3-11x12-6x22-6x32
127

отрицательно определѐнная. |
|
|
|
|
|||||
Решение. |
|
|
|
|
|
|
|
|
|
1=-11<0; |
|
2= |
|
11 |
6 |
|
66 36 30 0 |
, |
|
|
|
|
|||||||
|
|
6 |
6 |
|
|||||
|
|
|
|
|
|
|
|
||
|
|
6 |
6 |
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|||
3 |
6 |
6 |
3 |
|
|
81 0 . |
|
||
|
|
|
|
|
|
|
|
|
|
|
6 |
3 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7.4. Приведение общего уравнения кривой второго порядка к каноническому виду
Установим на плоскости прямоугольную декартову систему координат и рассмотрим общее уравнение второй степени:
a |
11 x |
2 |
+2a |
x x |
+a |
22 x |
2 +2a x |
+2a x |
+a=0. |
(7.2) |
|
|
|
|
12 1 2 |
|
2 |
1 1 |
2 2 |
|
|
||
|
1 |
|
|
|
|
|
|
|
|
||
Множество точек, координаты которых удовлетворяют уравнению (7.2), называется линией (или кривой) второго порядка.
Таким образом, общее уравнение кривой второго порядка имеет вид (7.2). Старшая группа членов:
|
a |
11 x |
2 +2a |
12 |
x x |
+a |
22 x |
2 |
, |
|
|
|
|
|
|
1 2 |
|
2 |
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
||
является |
квадратичной |
|
формой |
относительно |
текущих |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
координат. |
Обозначим |
через |
e 1, |
e 2 |
|
единичные |
векторы, |
||||
направленные по осям координат. Как было показано в предыдущем параграфе, квадратичная форма, соответствующая группе старших членов в уравнении (7.2), в
|
|
|
|
|
|
|
|
некотором ортонормированном же базисе e1 |
,e2 приводится к |
||||||
сумме квадратов |
1 x 2 |
+ |
2 x 2 |
, где |
1, 2 - собственные значения |
||
|
|
1 |
|
2 |
|
|
|
матрицы A |
a11 |
a12 |
, |
|
|
- орты соответствующих им |
|
a21 |
a22 |
а e1 |
,e2 |
||||
|
|
|
|
|
|
||
собственных векторов.
128

Теперь, используя |
формулы |
перехода от |
координат |
|
|
|
|
|
|
вектора в старом базисе |
( e 1, |
e 2) |
к координатам |
этого же |
|
|
|
|
|
|
|
|
|
|
|
), X=TX'’, получаем следующее |
|||||
вектора в новом базисе ( e |
,e |
|||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
уравнение кривой второго порядка: |
|
|
|
|
|
|||||||||||
|
1 x |
2 |
+ |
2 x |
2 |
+2(a |
t |
11 |
+a t |
) x |
+2(a t |
+a t |
) x |
2 |
+a=0. (7.3) |
|
|
|
|
2 |
1 |
|
|
2 21 |
1 |
1 12 |
2 22 |
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь |
T |
|
t11 |
t12 |
- матрица перехода от старого базиса к |
|||||||||||
|
t21 |
t22 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
новому, т.е. матрица, столбцами которой являются координаты
|
|
|
|
|
|
|
ортов |
( e1 |
,e2 |
) |
собственных векторов матрицы |
A в базисе |
|
|
|
|
|
|
|
|
e |
1, e 2. |
Это |
|
уравнение уже не содержит |
произведения |
|
координат и, следовательно, может быть приведено к каноническому виду путѐм выделения полного квадрата по x1
и x2 . Итак, исследование кривых второго порядка, заданных
общим уравнением, проводится по следующей схеме: 1.Записывают симметрическую матрицу
соответствующую группе старших членов уравнения. 2.Находят собственные значения и собственные
векторы этой матрицы.
3.Вводят новые координаты, взяв в качестве нового базиса орты собственных векторов матрицы A. Введение нового базиса равносильно повороту системы координат на некоторый угол .
4.После введения нового базиса, при котором исчезнут произведения текущих координат, общее уравнение кривой примет вид (7.3).
5.Выполняя параллельный перенос координатных осей нового базиса, получаем каноническое уравнение кривой второго порядка.
Определить новое начало координат при параллельном переносе можно, выделив полные квадраты по x1 и x2 . В полученном каноническом уравнении возможны следующие
129

случаи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
1 |
2>0. |
|
|
|
|
|
|
В этом случае мы имеем уравнение |
||||||||||||||||||||||||||||||
эллипса |
|
|
(действительного или мнимого). |
|
|
|
|
||||||||||||||||||||||||||||||||
2) |
1 |
2<0. |
|
|
|
|
|
|
В |
этом |
случае |
мы |
|
имеем уравнение |
|||||||||||||||||||||||||
гиперболы |
|
(или |
|
|
пара прямых, если свободный член |
||||||||||||||||||||||||||||||||||
канонического |
|
|
уравнения равен нулю). |
|
|
|
|
||||||||||||||||||||||||||||||||
3) |
1=0 или |
|
|
2=0. |
|
В этом случае мы имеем уравнение |
|||||||||||||||||||||||||||||||||
параболы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Привести к каноническому виду уравнение |
|||||||||||||||||||||||||||||||||||||||
кривой x1x2=a и построить эту кривую. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1.Записываем |
|
|
симметрическую |
|
|
матрицу, |
|||||||||||||||||||||||||||||||||
порождающую квадратичную форму A |
|
|
|
|
|
|
0 |
|
1/ 2 . |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ 2 |
|
0 |
|
|
||||||
2. Находим собственные значения и собственные |
|||||||||||||||||||||||||||||||||||||||
векторы этой матрицы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
2 |
|
|
|
0 ; 2 |
|
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
. |
|||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
1 |
2 |
2 |
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Для нахождения e1 |
|
,e2 |
составляем системы уравнений: |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
l |
|
|
1 |
m 0 , |
|
|
|
1 |
l |
|
|
|
1 |
|
m 0 , |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
2 |
|
1 |
2 |
1 |
|
|
|
и |
2 |
|
|
2 |
|
2 |
|
|
|
2 |
|
. |
|
|
|||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
l |
|
|
m 0 , |
|
|
|
|
l |
|
|
m 0 . |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
2 |
|
|
1 |
2 |
|
1 |
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|||||||||||||
В первой системе, полагая m1=1, получаем l1=1, и, |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
следовательно, e =(1,1) ; e |
|
|
|
|
|
|
, |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Аналогично, во второй системе полагая m2=1, получаем l2= -1, следовательно,
130
