Учебное пособие 1920

А. А. Катрахова, В. С. Купцов, Е. М. Васильев

СПЕЦГЛАВЫ МАТЕМАТИКИ И ИХ ПРИЛОЖЕНИЯ К ЗАДАЧАМ ЭЛЕКТРОМЕХАНИКИ

И ТЕОРИИ УПРАВЛЕНИЯ

Курс лекций

Воронеж 2019

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Воронежский государственный технический университет»

А. А. Катрахова, В. С. Купцов, Е. М. Васильев

СПЕЦГЛАВЫ МАТЕМАТИКИ И ИХ ПРИЛОЖЕНИЯ К ЗАДАЧАМ ЭЛЕКТРОМЕХАНИКИ И ТЕОРИИ УПРАВЛЕНИЯ

Курс лекций

Воронеж 2019

УДК 517.53 (075.8) ББК 22.1я7

K29

Рецензенты:

кафедра математического и прикладного анализа Воронежского государственного университета

(зав. кафедрой д-р физ.- мат. наук, проф. А. И. Шашкин); д-р техн. наук, проф. Н. Д. Вервейко

Катрахова, А. А.

Спецглавы математики и их приложения к задачам К29 электромеханики и теории управления: курс лекций / А. А. Катрахова, В. С. Купцов, Е. М. Васильев; ФГБОУ ВО «Воронежский государственный технический

университет». – Воронеж: Изд-во ВГТУ, 2019. - 268 c.

ISBN 978-5-7731-0802-3

В издании содержится теоретический материал и задачи по дисциплине «Спецглавы математики».

Предназначено для студентов, обучающихся по направлениям 27.03.04 «Управление в технических системах», 13.03.02 «Электроэнергетика и электротехника» (все профили).

Ил. 90. Табл. 48. Библиогр.: 14 назв.

УДК 517.53 (075.8) ББК 22.1я7

Печатается по решению учебно-методического совета Воронежского государственного технического университета

ISBN 978-5-7731-0802-3 Катрахова А. А., Купцов В. С.,

Васильев Е. М., 2019

ФГБОУ ВО «Воронежский государственный технический университет», 2019

2

ВВЕДЕНИЕ

Курс лекций содержит теоретический материал и задачи по дисциплине «Спецглавы математики».

Содержание данной работы соответствует программе курса математики для бакалавров инженерно-технических специальностей вузов, утвержденной Министерством науки и высщего образования Российской Федерации в соответствии с

новыми образовательными стандартами.

Издание состоит из трех частей: уравнения математической физики, элементы вариационного исчисления и элементы

дискретной математики.

УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

1. ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

1.1. Уравнение колебаний струны

Пусть струна закреплена на концах (рис. 1.1). Струной называется тонкая нить (без сопротивления при изгибе и с неменяющейся длиной). Сила натяжения Т(x) струны будет определяющей, и не учитывается сила тяжести струны.

Рис. 1.1. Схема струны, закреплённой на концах

В положении равновесия струна направлена по оси Ох. Рассматриваются поперечные колебания струны (движение струны будет в одной плоскости m, и точки струны перемещаются вдоль оси Оu) (рис. 1.1).

3

Пусть u(х, t) - перемещение точек струны из положения равновесия. Рассматриваются малые колебания струны, при

этом u(х, t) и производная ди будут малыми (их квадратами и

дх

произведениями можно пренебречь).

Рассмотрим участок (х1, х2) (рис. 1.1). Струна имеет в этом случае положение М1,М2, и ее длина в момент времени t:

x2

S 1 ux2 dx x2 x1 S.

x1

Для малых колебаний участков струны не будет удлинений. По закону Гука натяжение Т для точек струны не меняется со временем. Будем рассматривать в этом случае поперечные колебания струны. Силы инерции и внешние силы будут параллельны оси Оu. Проекция сил на ось Ох будет T x1 cos x1 T x2 cos x2 0 (α(х) - угол между касательной в точке с абсциссой х к струне с положительным направлением оси х). Имеем

Проекция на ось Оu сил натяжения для точек М1 и М2 равняется Y T0 sin x2 sin x1 , и так как

4

x2 2u

Имеем Y T0 dx.

x1 x2

Пусть р(х,t) - внешняя сила струны (направлена вдоль оси Оu и меняется по длине). Проекция на ось Оu этой силы на участке М1М2 струны равна

x2

p x,t dx.

x1

Введем ρ(х) линейную плотность струны. Сила инерции участка М1М2 струны

x1

t

Из условия равновесия струны проекция всех сил на ось Оu на участке М1М2 струны равна нулю:

И так как х1 и х2 произвольны, то подынтегральная функция равна нулю в произвольный момент времени t:

Получим уравнение колебаний струны.

При ρ=const для однородной струны уравнение имеет вид

Если р(х,t)=0, имеем свободные колебания струны и

5

Уравнение будет иметь бесчисленное множество частных решений. Необходимы дополнительные условия, определяемые физическим смыслом задачи. В начальный момент времени (t=0) зададим положение и скорость точек струны:

Условия будем называть начальными условиями. Для ограниченной струны задаются условия на ее концах. Если стру-

на закреплена, то на концах u x 0 0, u x l 0 при t ≥ 0, и это

будут краевые или граничные условия.

Можно также исследовать колебания полубесконечной или бесконечной струны (один или оба конца бесконечны).

Для первого случая граничное условие u x 0 0, а для второго

случая граничных условий не будет, а начальные функции будут φ0(х) и φ1(x) для всех 0≤x<∞ или для всех ∞< х <∞.

1.2.Решение задач о колебаниях бесконечной

иполуограниченной cтруны (метод Даламбера)

А. Рассмотрим бесконечную струну (в состоянии равновесия она совпадает с осью Ox (- <x< )) . В начальный момент времени t 0 для точек струны задаются начальные отклонения и начальные скорости. Найдем отклонение

для x ( , ), t 0 и начальных условий

u(t,x) t 0 (x),

u(t,x)

t 0 (x),t

6

u( , ) C( ), или u( , ) C1( ) C2 ( ), где C1( ),C2 ( )- про-

извольные функции от одной переменной.

Решение нашего уравнения можно представить в виде u(t,x) C1(x at) C2(x at), и теперь необходимо найти функ-

ции C1( ),C2 ( ) так, чтобы были выполнены начальные усло-

вия. Для вычисления функций C1( ),C2 ( ) имеем систему уравнений

С1(x) C2 (x) (x);

a C1(x) C2 (x) (x).

Интегрируя второе уравнение в пределах от 0 до x , получим:

7

C1(x) C2(x) (x);

Из этой системы уравнений имеем:

Решение задачи о колебаниях бесконечной струны будет:

u(t, x) C1 (x at ) C2 (x at )

Эта формула называется формулой Даламбера.

Физическая интерпретация формулы Даламбера

Два частных случая колебания бесконечной струны:

1) для колебаний выполнено: начальное отклонение

(x) , начальные скорости (х) 0 ;

2)начальные отклонения (х) 0 , начальные скорости

(х) 0 .

8

В первом случае решением задачи будет выражение

u(t,x) (x at) (x at) . 2

x

x

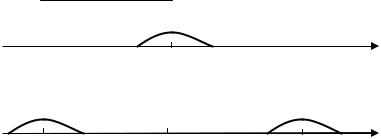
Рис. 1.2. Начальная форма струны

x

Рис. 1.3. Форма струны в момент времени t

Если начальная форма струны имеет вид (рис. 1.2), то в момент времени t форма струны будет (рис. 1.3).

Т. е. возмущение струны для точки x распространяется вправо и влево со скоростью a по величине в два раза меньше. При прохождении полуволны точки струны возвращаются в положение равновесия. Отклонение точки x в момент времени t вычисляется сложением отклонений точек x at и x at в начальный момент времени (уменьшенные вдвое).

Во втором случае решение задачи имеет вид:

9