Учебное пособие 1851

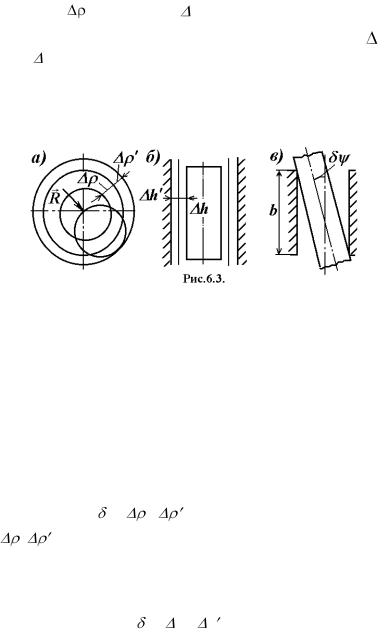
кинематической пары определяется ошибками изготовления

радиуса вала и отверстия ~ для вращательной пары (рис.

ρ

~

6.3а) и ошибками половины ширины направляющей h и ползуна h (рис. 6.3б) для поступательной кинематической пары.

Количество ошибок, приводящих к неточности расположения элемента пары, равно числу связей, налагаемых парой

на относительное движение звеньев. Так, например, положение элемента вращательной V класса пары определяется в пространстве координатами точки контакта звеньев на цилиндре вала или отверстия (три линейных величины) и положением этой оси (две угловых величины), то есть пятью величинами. Ошибки положения элементов звеньев являются первичными, поскольку возникают при изготовлении механизма. Эти ошибки растут по мере эксплуатации механизма за счет износа элементов звеньев.

Для вращательной кинематической пары модуль линейной ошибки

где h, h- ошибки полуширин охватывающего и охватываемого элементов звеньев.

Кроме рассмотренных линейных ошибок l кинематические пары могут давать ошибки направления с модулем

= / - /,

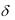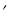где , - действительный и теоретический углы, характеризующие положение одного из звеньев, соединенных кинематической парой, относительно другого.

Если b – ширина охватывающего элемента кинематической пары, а l – линейная ошибка этой пары, то в силу малости углов (рис. 6.3в)

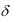max = arctg(2 l /b) = 2 l /b.

Направление относительного смещения звеньев определяется направлением реакций в кинематической паре. Поэтому ошибки расположения элементов кинематических пар являются векторами. Если модули векторов ошибок определяются ошибками изготовления, то направления этих векторов могут быть определены только силовым расчетом. Следовательно, расчету ошибок механизма, вызванных первичными ошибками, должен предшествовать силовой расчет механизма.

2.6. 6.3. 3акон распределения ошибок

Ошибки величин случайной природы задаются законами распределения этих величин. Значение случайной величины

97

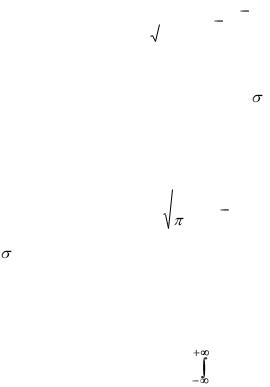
определяется только с некоторой вероятностью методами теории вероятностей.

Закон распределения случайной величины задает алгоритм определения вероятности, с которой случайная величина принимает некоторое значение.

Законы распределения ошибок изготовления звеньев и элементов звеньев, как случайных величин, определяются многими факторами. Наиболее часто встречается закон равной вероятности (рис. 6.4а) P(x) = const и нормальный закон (закон Гаусса) (рис. 6.4б)

где Р (х) – вероятность, с которой случайная величина Х принимает значение х, а – математическое ожидание случайной величины Х, т.е. ее среднее значение, - среднеквадратическое отклонение случайной величины от ее математического ожидания.

Распределение случайных электрических или электромагнитных величин описывается законом Максвелла

где о – среднеквадратическое отклонение для исходного нормального распределения, на основе которого строится распределение Максвелла.

Математическое ожидание непрерывной случайной величины

a = M{x} = х p(x)dx.

Для первичных ошибок математическое ожидание определяется по формуле

98

A=0,5 [gx+gn+ (gx - gn)]

где gx =max x, gn = min x – границы поля допусков величины х, - коэффициент асимметрии кривой функции распределения плотности вероятности (для нормального закона = 0) опре-

деляемый экспериментально.

о

Случайная величина Х = Х – а характеризует отклонение случайной величины Х от ее среднего значения а и называется центрированной случайной величиной.

Дисперсией случайной величины Х называется среднее

значение или математическое ожидание квадрата центриро-

о

ванной случайной величины Х

Величина (x) = D( x ) называется средним квадратиче-

ским отклонением случайной величины. Для практических це-

о

лей диапазон значений Х ограничивают так, чтобы вероят-

Область изменения х является отрезком с границами а

о

, где - коэффициент, зависящий от ( х ), равный трем для нормального распределения. Случайная величина с ограниченной областью изменения называется усеченной.

6.4. Аналитический метод определения конечных 2.7. ошибок механизма

Этот метод имеет смысл применять в случаях, когда известно, аналитическое выражение для функции положения выходного звена. При этом может быть явное или неявное задание этой функци.

99

Положение выходного звена ММ в неподвижной системе

o

Z задается векторной величиной – вектор - радиусом- r не-

которой характерной точки схвата (например центра масс), ис-

o

ходящим из начала отсчета системы Z , и углами поворота схвата относительно осей этой системы. Конечным углам поворота выходного звена нельзя поставить в соответствие век-

равны этим углам. Таким образом, положение и ориентация схвата определяется шестью скалярными величинами, только три из которых образуют вектор.

Пусть положение характерной точки схвата определено в

o

системе Z векторной функцией

матрицы, определяющие обобщенные координаты звеньев механизма qi и их длины li и другие характеристики положения звеньев.

Элементы ~i являются матрицами, определяющими размеры и положения элементов звеньев относительно звеньев. Ошибка ~i

ров и реакциям в кинематической паре, получаемым из силового расчета идеального механизма.

Пусть qi , li , ~i (i=0,1, …, n) – ошибки величин qi , li и ij , а r - приращение вектора r , вызванное этими ошибками.

Тогда

Обычно ошибки величин малы в сравнении с самими величинами и, поэтому, в разложении r в ряд Тейлора можно учесть производные до второго порядка включительно. Для

Если здесь пренебречь слагаемыми, содержащие вторые производные от r , что возможно вследствие малости 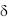k в сравнение с k, то выражение

будет конечной ошибкой положения характерной точки схвата.

Теория точности, использующая выражение (2), называется линейной теорией точности. В большинстве случаев эта теория дает практически приемлемые результаты при не слишком больших 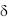k.

Частная производная r /k называется коэффициентом влияния, так как характеризуют влияние единичной ошибки

Поворот звена относительно трех взаимно перпендикулярных осей координат на конечные углы нельзя охарактеризовать вектором угла поворота. Подобный вектор можно использовать только при бесконечно малых углах поворота. Поэтому для оценки ошибок углов поворота звена можно использовать

101

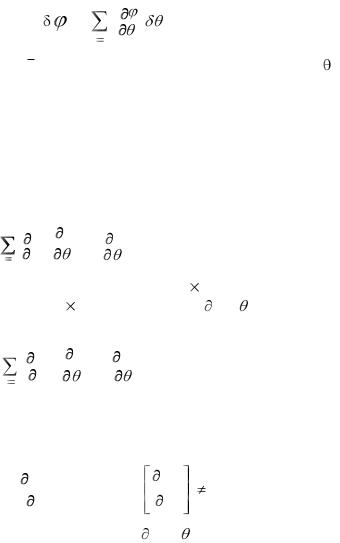
только матрицу ориентации, которая, может быть получена также, как и формула (2):

Если вектор r явно не выражается через параметры k (что обычно наблюдается для замкнутых кинематических цепей), то определяется соотношение

Таким образом, получена система 3 5m уравнений, линейных относительно 3 5m неизвестных rj /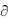k . Эта система распадается на 5m групп по три уравнения в каждой группе

Система (6) неоднородна, поэтому она будет разрешимой только если соответствующий ей определитель матрицы Якоби (якобиан)

После определения величин rj /k ошибки соответствующих выходных параметров механизма вычисляются по ранее полученным формулам (2) и (3).

102

По соотношениям (2), (3) можно определить зависимости выходных параметров позиционирования схвата от ошибок

6.5. Пример расчета точности механизма

Пусть необходимо определить ошибку положения плоского механизма (рис. 6.1), для которого длины звеньев l1 , l2 , и l3 их ошибки l1 , l2 , l3 известны. Положение точки D схвата определяется вектор - радиусом r , лежащим в плоскости движения механизма и определяется проекциями на оси системы z1, z2:

r1 = l1 cos q1 +l2 cos(q1 + q2) + l3 cos(q1+q2+q3 ), r2 = l1 sinq1 +l2 sin(q1 + q2) + l3 sin(q1+q2+q3).

Отсюда

и проекции вектора ошибки положения точки D на оси z1 , z2 определяется соотношениями

r1 = l1 cos q1 + l2 cos(q1 + q2) + l3 cos(q1+q2+q3 ), r2 = l1 sin q1 + l2 sin(q1 + q2 ) + l3 sin(q1+q2+q3 ).

103

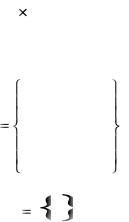
ПРИЛОЖЕНИЕ ОСНОВЫ АЛГЕБРЫ И АНАЛИЗА ВЕКТОРОВ И

МАТРИЦ ПРИМЕНИТЕЛЬНО К ТЕОРИИ ММ

Операции с векторами удобны при использовании аналитических методов исследования ММ. При построении программ вычислений, основанных на операциях с векторами, требуется использовать координатное описание векторов и, поэтому становится существенно необходимым использование матричного аппарата. Ниже приводятся необходимые операции с матрицами.

Матрицей порядка m n называется прямоугольная таблица чисел, имеющая m строк и n столбцов. Матрицы обозначаются большими латинскими и греческими буквами, а их элементы – малыми буквами. Например

a11a12 ....a1n A a21a22 ....a2n

.......... ..........

am1am2 ....amn

или более кратко

A aij ( mxn ) ,

где a ij - элемент матрицы A ; i, j - номера строки и столбца соответственно, содержащие элемент aij .

Частным случаем матрицы является матрица – столбец (или просто столбец)

104

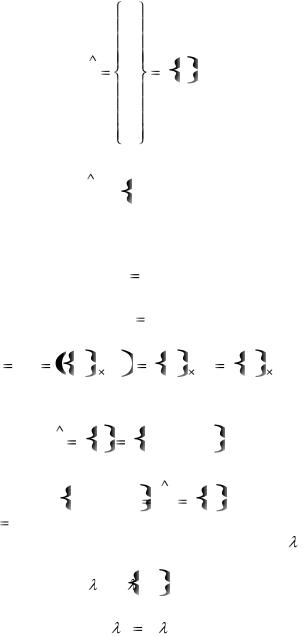
b1 b2

.

bn

и матрица – строка (или просто строка)

bT a1 ,a2 ,..., an

где «T » - символ операции транспонирования, то есть операции замены строк столбцами и наоборот.

ПУСТЬ

A 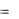aij ( mxn ) .

Умножение матрицы на скаляр коммутативно, то есть

A A .

105