Учебное пособие 1851
.pdf
Сложением матриц A и B называется операция суммирования элементов матриц A и B с одинаковыми индексами. Сложение матриц определено только для матриц одинаковых размеров. По определению, если
A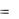 
aij ( m n ) ,B bij ( m n )
и
|
C |
A B, |
|
|
то |
|
|
|
|
C cij |
( m n ) |
aij |
bij |
( m n ) . |
Сложение матриц коммутативно и ассоциативно, то есть |
||||
|
A B |
B |
A |
|
и |
|
|
|
|
A ( B C ) ( A B ) C A B C.
Произведение матриц определено только при равенстве числа столбцов левой из перемножаемых матриц числу строк правой из перемножаемых матриц. Пусть
A aij |
( m n ) , B b jl |
( n k ) . |
|||
Произведением матриц A и B называется матрица |
|||||
C |
A B |
cil |
m k , |
||
где |
|
|
|
|
|
|
cil |
n |
aijb jl , |
|
|
|
|
|
|||
|
|
j |
1 |
|
|
то есть элемент cil матрицы C равен сумме произведений
элементов aij и b jl матриц, стоящих в i - той строке матрицы A и в l - том столбце матрицы B .
Некоторый столбец с номером l матрицы B можно ото-
ждествить с матрицей – столбцом bl размером n , то есть
106
bl b jl |
n . |
Аналогично строку матрицы A с номером i можно отождествить с матрицей столбцом
ai ai1 ,ai2 ,..., ain T |
aij n . |
Скалярным произведением матриц ai и bl называется число, определяемое выражением
|
n |
aiT bl . |
( ai bl ) |
aija jl |
|
j |
1 |
|
Поэтому элемент матрицы C |
A B равен |
|
cil |
( ai bl ), |
|
произведение матриц имеет следующие свойства: некоммутативность
A 
B B 
A;
ассоциативность
( A
B )
C A
( B 
C ) A
B 
C;
дистрибутивность
A
( B C ) A
B A
C.
Если
A |
aij |
|
|
( m n ) |
|
и |
|
|
b |
b j |
n , |
то произведение матриц A и b является матрица - столбец c размерности m , то есть
c A
b .
107
Если какой либо из элементов матрицы A зависит от некоторого аргумента t , то матрица A является функцией этого аргумента, то есть
A A( t ) |
|
aij ( t ) ( m n ) . |
||||
Если все элементы матрицы A |
интегрируемые (диффе- |
|||||
ренцируемые) функции аргумента t |
во всех точках его облас- |
|||||
ти определения, то интеграл (производная) от матрицы A есть |
||||||
матрица той же структуры, что и A , получаемая заменой каж- |
||||||
дого элемента матрицы A интегралом (производной) от этого |
||||||
элемента, то есть |
|
|
|
|
|
|
|
|
ij |
dt ( m n ) |
|
||
A |
a |
|
|
|||
и |
|
|
|
|
|
|
Adt |
|
aij dt |
( m n ) |
. |
||
|
|
|
|
|
||
Производная и интеграл от произведения матриц имеют те же свойства, что и производная и интеграл от произведения функций. Легко доказать, что если
|
A |
|
const, |
|
|
|
то |
A |
|
0, |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
( AB( t )) AB( t ), ( B( t )A ) |
B( t )A, |
|||||
|
|
|
|
|
|
|
( C( t ) B( t )) |
C( t ) B( t ), |
|||||
|
|
|
|
|
|
|
( C( t )B( t )) |
C( t )B( t ) C( t )B( t ) ( B( t )C( t )) , |
|||||
|
|
|
|
|
|
|
|
Adt |
|
A |
dt |
At , |
|
|
AB( t )dt |
|
A B( t )dt, |
|||
|
B( t )Adt |
|
( |
B( t )dt )A, |
||
( C( t ) |
B( t ))dt |
|
|
C( t )dt |
B( t )dt, |
|
C( t )B( t )dt |
|
B( t )C( t )dt, |
||||
B( t )dt |
d( B( t )) |
B( t ), |
||||
|
|
|
|
|
|
|
|
|
108 |
|
|
||
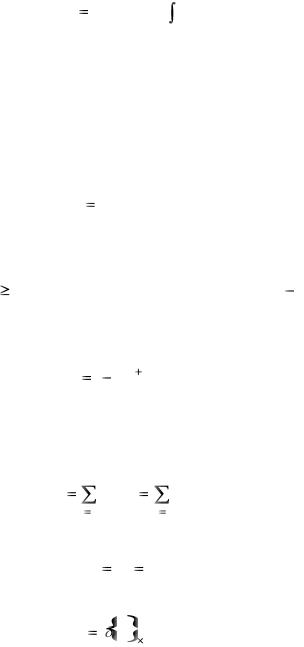
B( t )d( C( t )) B( t )C( t ) 
( dB( t ))C( t )
- формула интегрирования по частям.
Легко видеть, что матрицы дифференцируются и интегрируются также как и обычные функции, с той разницей, что нельзя менять местами сомножители в дифференцируемом и интегрируемом произведении матриц.
Для квадратной матрицы A можно вычислить определитель этой матрицы
|
|
|
a11a12 |
....a1n |
|
|
|
|
det A |
a21a22 |
....a2n |
. |
|
|
|
.......... .......... .. |
|
|||
|
|
|
|
|
||
|
|
|
an1an2 |
....ann |
|
|
Минором |
M ij |
элемента aij определителя det A матрицы |
||||
A порядка n |
2 называется определитель порядка n |
1 , по- |
||||
лучаемый из |
det A |
вычеркиванием i - той строки и |
j - того |
|||
столбца, на пересечении которых стоит элемент aij . Число
Aij ( 1 )( i j ) M ij
называется алгебраическим дополнением элемента aij . Определитель матрицы A можно представить в виде сум-
мы произведений элементов некоторого столбца (некоторой строки) матрицы A на их алгебраическое дополнение, то есть
n |
|
n |
det A |
aij Aij |
aij Aij . |
i 1 |
|
j 1 |
Единичной матрицей порядка |
n называется матрица I , |
|
такая, что для любой матрицы A порядка n |
||
AI |
IA |
A. |
Все элементы матрицы I , стоящие на главной диагонали, равны единице, а прочие элементы равны нулю, то есть
I |
i |
, |
j ( n m ) |
||
|
109 |
|
где
i |
1,при |
i |
j |
- символ Кронекера. |
|
|
|
|
|
||
j |
0,при |
i |
j |
|
|
|
|
||||
|
|
|
|||
Матрица A порядка n |
n называется вырожденной, если |
||||
ее определитель порядка n равен нулю. |
|
||||
Обратной матрицей для невырожденной матрицы |
A по- |
||||
рядка n n называется матрица A 1 того же порядка, |
такая, |
||||
что |
|
|
|
|
|
AA 1 A 1 A I .
Вырожденная матрица обратной матрицы не имеет. Для любой невырожденной матрицы A обратная матрица
определяется по формуле
B bij |
|
A 1 |
1 |
|
a ji |
( n n ) |
|
|
|||
|
|
||||
|
|
det A |
( n n ) |
||
|
|
|
|
||
иявляется единственной.
Вкинематике и динамике ММ используются в основном
трехмерные векторы и квадратные матрицы порядка 3 3 . Поэтому ниже индексы элементов матриц и компонентов векторов принимают значения 1, 2 и 3, если особо не оговорено противное.
Вектору r может быть поставлена в соответствие матрица
– строка |
|
|
|
|
|
|
|
||||
|
|
|
|
rT |
r1 ,r2 ,r3 |
|
|
|
|||
или матрица – столбец |
|
|
|
|
|
|
|
||||
|
|
|
|
r |
r1 ,r2 ,r3 T , |
|
|
|
|||
где ri ( i 1,2,3 ) - проекции вектора |
|
|
|
на оси некоторой сис- |
|||||||
r |
|||||||||||
темы координат. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
Скалярное произведение векторов r |
и p |
||||||||||
|
|
|
|
3 |
piri ( p r ) pT r . |
||||||
( p r ) |
|||||||||||
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторное произведение векторов |
p и r |
|||||||||||||||||
|
|
|
|
|
|
|
|
( p2 r 3 |
p3r 2 ) |
|
1 |
|
( p3r1 |
|||||
|
S |
p |
r |
e |
||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
(1) |
|||
|
|
p1r 3 ) |
e |
( p1r 2 |
p2 r1 ) |
e |
, |
|
|
|
||||||||
где e j - орты осей системы координат Z , в которой определены проекции p и r .
Пусть для некоторой матрицы |
построена матрица |
|
|||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
D( |
) |
|
|
|
3 |
|
0 |
|
|
|
|
1 |
|
, |
|
|
(2) |
|
|||||
|
|
|
|
|
2 |
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где j - проекции |
|
|
на оси системы Z . |
|
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||||
Очевидно, что D( |
) |
|
|
D( |
). Векторное произведение (1) |
||||||||||||||||||
можно заменить матричной операцией |
|
|
|||||||||||||||||||||
|
S |
|
D( p ) r |
|
|
|
D( r ) p . |
(3) |
|
||||||||||||||
Двойное векторное произведение |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
c |
( p |
|
r ) |
c |
|
S |
(4) |
|
|||||||||||
также может быть записано через операции с матрицами |
|
||||||||||||||||||||||
|
d |
D( c ) S |
|
D( c )D( p ) r . |
(5) |
|
|||||||||||||||||
Если ввести матрицу |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
( c3 p3 |
|
|
c2 p2 ) |
|
|
|
|
c2 p1 |
c3 p1 |
|
||||||||||||
D( c, p ) |
|
c1 p2 |
|
|
|
|
|
( c3 p3 |
c1 p1 ) |
c3 p2 |
, |
||||||||||||
|
|
c1 p3 |
|
|
|
|
|
|
|
c2 p3 |
( c2 p2 c1 p1 ) |
|
|||||||||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
~ |
|
D( c, p ) r . |
(6) |
|
||||||||||
D( c )D( p )r |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
111 |
|
|
|
|
|
|
|
|||
2.8.СПИСОК ЛИТЕРАТУРЫ
1.Белянин П.Н. промышленные роботы и их применение: Робототехника для машиностроения. 2-е изд. перераб.
идоп. – М.: Машиностроение, 1983 – 311 с.: ил.
2.Бурдаков С.Ф., Дьяченко В.А., Тимофеев А.Н. Проектирование манипуляторов промышленных роботов и роботизированных комплексов. – М.: Высшая школа,
1986 – 264с.: ил.
3.Козырев Ю.Г. Промышленные роботы: Справочник – М.: Машиностроение, 1983 – 376 с.: ил.
4.Левитская О.Н., Левитский Н.И. Курс теории механизмов и машин. – М.: Высшая школа, 1978 – 265с.: ил.
5.Вукобратович М., Стокич Д. Управление манипуляционными роботами: теория и приложения. – М.: Наука,
1985. – 384 с.: ил.
6.Механика промышленных роботов: Уч. пособие для втузов: В 3 кн. Под ред. К.В. Фролова, Е.М. Воробьѐва.
– М.: Высшая школа, 1988.
7.Методические указания к разделу курса прикладной механики «Манипуляционные механизмы» для студентов специальности 210300 дневной и вечерней форм обучения. Воронеж. гос. техн. ун - т. Сост.:, Д. В. Хван, В. А. Рябцев, В. Н. Потапов. Воронеж, 2000.
8.Методические указания к решению задач по курсу прикладной механики для студентов специальности 210300 всех форм обучения. Воронеж. гос. техн. ун - т. Сост.:, В. А.Рябцев, В. В. Елисеев, В. Н. Потапов. Воронеж,
2000.
112
ОГЛАВЛЕНИЕ |
|
Предисловие |
3 |
Введение. Предмет, значение и задачи раздела |
|
«Манипуляционные механизмы» (ММ) |
4 |
2.9. |
Рол |
ь промышленных роботов (ПР) и манипуляторов |
|
2.10. |
(П |
М) в обеспечении технического прогресса |
4 |
2.11. |
Осо |
бенности ПР как средства автоматизации |
5 |
2.12. |
|
роизводственных процессов |
|
2.13. |
|
ели и задачи раздела «Манипуляционные |
|
2.14. |
ме- |
ханизмы» |
5 |
2.15. |
Свя |
зь раздела с другими дисциплинами |
6 |
1. СТРУКТУРНЫЙ АНАЛИЗ МАНИПУЛЯЦИОННЫХ МЕ-
ХАНИЗМОВ |
7 |
2.16. |
1.1. |
Кинематические пары |
7 |
2.17. |
1.2. |
Кинематические цепи |
10 |
2.18. |
1.3. |
Степень подвижности кинематической цепи |
11 |
2.19. |
1.4. |
Структурная и кинематическая |
|
2.20. |
схе- |
мы механизма |
13 |
4 |
|
2.21. |
1.5. |
Замена кинематических пар k-того класса |
|
2.22. |
эк- |
вивалентными кинематическими цепями |
14 |
2.23. |
1.6. |
Структурный анализ и синтез механизмов |
15 |
2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МЕХАНИЗМА |
17 |
2.24. |
2.1. |
Базовая и связанная системы координат |
17 |
2.25. |
2.2. |
Преобразование проекций векторов |
17 |
2.26. |
2.3. |
Математическая модель кинематической схемы |
22 |
2.27. |
2.4.C |
борка механизма |
25 |
2.28. |
2.4.1. |
Первый способ сборки |
26 |
2.29. |
2.4.2. |
Второй способ сборки |
31 |
3. ХАРАКТЕРИСТИКИ МАНИПУЛЯЦИОННЫХ МЕХА- |
|
НИЗМОВ |
38 |
2.30. |
3.1. |
Маневренность ММ |
38 |
2.31. |
3.2. |
Рабочая зона и классификация движений схвата |
39 |
2.32. |
3.3. |
Угол и коэффициент сервиса ММ |
40 |
2.33. |
|
.4. Определение коэффициента сервиса |
|
5 |
|
2.34. |
ме- |
тодом объѐмов |
41 |
2.35. |
3.5. |
Мобильность ММ |
44 |
4. КИНЕМАТИЧЕСКИЙ АНАЛИЗ МАНИПУЛЯЦИОННЫХ
МЕХАНИЗМОВ |
47 |
2.36. |
4.1. |
Задачи кинематического анализа ММ |
47 |
2.37. |
4.2. |
Формула Родриго |
47 |
2.38. |
4.3. |
Прямая задача о положении и ориентации |
|
2.39. |
схва- |
та |
49 |
2.40. |
|
.4. Обратная задача о положении и |
|
2.41. |
ори- |
ентации схвата |
51 |
2.42. |
4.5. |
Векторные уравнения кинематики ММ |
54 |
2.43. |
4.6. |
Матричные уравнения кинематики ММ |
60 |
2.44. |
4.7. |
Кинематический синтез ММ |
63 |
2.45. 5. Инерционные характеристики звена |
|
2.46. |
в |
пространственном движении |
65 |
6. ОСНОВЫ ТЕОРИИ ТОЧНОСТИ ПОЗИЦИОНИРОВАНИЯ
СХВАТА |
74 |
|
6 |