
Учебное пособие 1851
.pdf
-( i 1 |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
+ θ |
ε |
) |
|
|
|
|
|
|
|
|
-( |
||||||||||||||
r |
1,i |
|||||||||||||||||||||||||
αi |
1, j q j |
|
|
|
i 1 |
|
0 |
|
|
|
|
|
|
|
i |
|
|
|
||||||||
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ei )+ |
|
|
|
|
|
|||||||||||||
+ θi 1 + qi ( |
|
|
|
|
|
|
|
ε0 ) |
|
,i |
||||||||||||||||
|
|
|
|
|
|
|
ri |
|||||||||||||||||||
|
|
i 1 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
= α |
|
|
|
|
|
|
|
|
= e |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
ii |
ii |
|
|
r |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
i,i |
|
|
|
i |
|||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
1, j + αi |
||||||||||||
|
|
|
|
|
|
|
i j |
|
|
i |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1,i )+( |
||||
i |
1 |
ri |
|||||||||||||
+ |
|
|
|
( |
|
|
|
|
|
|
,i |
||||
|
|
i |
|
|
i |
ri |
|||||||||
|
|
,i , |
|
|
|
|
|
|
|
|
|
|
|||
ri |
|
|
|
|
|
|
|
|
|
|
|||||
1, j |
|
|
|
|
1,i , |
(i |
|||||||||
|
|
i |
|||||||||||||
i = i 1 +( θi 1 + ε0 ) i 1,i + qi ( i 1
i 1,i + qi ( i 1 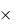
i
αij j 1
).
j),
ei )
q j +
(5.14)
ri,i +
+ i ( i ri,i )- i 1 ( i 1 ri 1,i )
при i 0.
Соотношения (10) – (14) также являются рекуррентными и для их использования необходимо определить характеристики
ε0 , W0 , θ0 , 0 базового звена.
Для поступательной 0,1 кинематической пары
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε1 = |
ε |
0 |
, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 = |
|
0 , |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
e |
+ 2 q |
|
|
|
|
|
|
e |
)+ |
|
|
|
|
|
|
||||||||
W |
= W |
+ q |
|
( |
|
|
|
|
|
ε |
|
|
|
|
+ |
||||||||||||||||
0 |
0 |
0,1 |
|||||||||||||||||||||||||||||
1 |
0 |
1 |
1 |
|
1 |
|
|
1 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
0,1 ) , |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где индексом 0 помечены кинематические характеристики базового звена и его центра масс.
Отсюда и из (8) и (9) следует
ε1 = α11 q1 + θ1 + ε0 = ε0 ,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 2 q |
|
|
|
|
||||
|
|
= β |
q + |
|
|
|
|
|
|
|
|
|
|
+ q |
e |
|
|
|
e )+ |
||||||||||
W |
|
|
+ W |
= W |
|
( |
|
|
|||||||||||||||||||||
1 |
0 |
||||||||||||||||||||||||||||
1 |
11 |
1 |
|
|
0 |
0 |
1 |
1 |
1 |
|
1 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
+ |
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1). |
|
|
|
||||||
|
|
|
|
|
0 |
|
|
|
0,1 ++ |
|
|
0 ( |
|
0 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
76 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
Поскольку α11 |
= 0, |
|
|
|
β11 = e1 , |
|
θ1 = θ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
= |
|
|
|
|
+ ( |
θ0 |
+ |
ε0 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)+ 2 |
|
|
|
|
( |
|
|
|
|
|
|
|
|
e1 |
), |
||||||||||||||||||||||||||||||||||
1 |
|
0 |
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0,1 |
|
|
|
|
0 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
=0, |
|
|
θ0 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.15) |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Для вращательной кинематической пары |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e1 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
q1 e1 |
|
|
|
ε1 |
|
|
|
|
ε0 |
|
|
|
|
|
|
|
|
q1 e1 |
|
|
|
q1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
), |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)+ ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
W |
|
|
=W |
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
+ q |
+ |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
r |
|
|
|
|
0 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ q1 ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
e1 )) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
r1,1 + |
1 |
|
|
|
|
|
|
1 |
|
|
|
r1,1 ). |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
ε1 |
= |
|
α11 q1 |
|
+ |
|
|
θ1 |
+ |
|
|
ε0 |
= |
ε0 |
+ |
|
|
q1 e1 |
+ |
|
( |
|
|
|
0 |
|
|
|
|
|
e1 |
) , |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
= |
|
|
β |
|
|
|
|
q |
+ |
|
|
|
|
|
|
|
+ W |
|
= W |
-( |
θ |
|
+ |
ε |
|
) |
|
|
|
|
|
|
- |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|
r |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
11 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
r |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
( |
θ0 |
+ |
ε0 |
+ |
|
|
q1 e1 |
+ |
|
|
|
|
|
( |
|
|
|
|
|
0 |
|
|
|
|
|
|
e1 |
)) |
|
|
|
|
r1,1 |
+ |
1 |
|
|
|
|
( |
|
|
1 |
|
|
|
r1,1 |
) , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
и получается |
|
|
|
|
|
|
=0, |
|
|
|
θ0 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Следовательно, независимо от типа 0,1 кинематической |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
пары |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
=0, |
|
|
|
|
|
|
θ0 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
По рекуррентным соотношениям (8) и (9) с учетом (10) – (14) по известным ε0 и W0 базового звена и обобщенным ско-
ростям qi и ускорениям qi входных звеньев ММ можно опре-
делить угловые скорости и ускорения и линейные скорости и ускорения центров масс любого звена ММ. Применительно к свату такая задача называется прямой задачей кинематики. ММ.
77
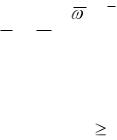
Обратная задача кинематики заключается в определении обобщенных скоростей qi и ускорений qi по заданным угло-
вым скорости и ускорению n , εn схвата и линейным скорости и ускорению Vn и Wn его центра масс. На основе полученных соотношений (1) – (3) и (4) – (7) можно составить 12 скалярных уравнений, содержащих 2(n+1) неизвестных qi и qi .
Если n=5, то полученная система уравнений может иметь единственное решение. При n 6 для получения единственного решения необходимо составить дополнительно 2(n-5) уравнения, описывающие какие-либо требования к механизму. Одним из таких требований может быть, например, обеспечение минимума кинетической энергии механизма, максимума значения коэффициента полезного действия (к. п. д.) и другие.
Существенной особенностью системы уравнений обратной задачи кинематики является ее нелинейность в целом, за счет наличия в уравнениях для ускорений вторых степеней qi .
Это обстоятельство, однако, не имеет существенного значения, поскольку рассматриваемая система расчленяется на две подсистемы. Одна из подсистем, получаемая из соотношений для скоростей, является линейной относительно qi и может быть
решена независимо от второй подсистемы.
После подстановки значений qi полученных из решения
первой подсистемы во вторую подсистему, эта подсистема становится линейной и также сравнительно легко решается.
Следует помнить, что прямая и обратная задачи кинематики решаются для данного положения механизма, то есть для заданных значений обобщенных координат.
4.6.Матричные уравнения кинематики ММ
Векторное описание кинематики ММ не удобно для программирования решения задач кинематики на компьютерах, поскольку этим задачам приходится давать скалярную форму-
78

лировку. Наиболее удобной для программирования решения задач на компьютерах является матричная формулировка и использование рекуррентных соотношений. Такая формулировка может быть получены из (5.1) – (5.3) или (5.4) – (5.7) путем замены операций над векторами их матричными аналогами.
ωi |
, |
εi |
ˆ |
ˆ |
i |
i |
|||
Пусть ˆ |
ˆ |
, V и W - трехмерные матрицы-столбцы про- |
||
екций угловых скорости и ускорения и линейных скорости и ускорения центра масс звена i, определенные в системе координат Zi. Пусть Li – матрица преобразования Zi-1 Zi. Для поступательной i-1,i пары имеем
|
|
|
|
|
ˆ |
=L |
ωˆ |
|
|
|
|
, |
ˆ |
|
=L |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.1) |
||||||||
|
|
|
|
ωi |
|
|
i |
i 1 |
|
εi |
|
|
|
i |
εi 1 , |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
rˆ ', |
i |
= rˆ |
|
+ qi eˆi , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
i |
|
|
i, i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
ˆ |
|
|
|
ˆ |
|
|
|
-D( |
ˆ |
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
eˆ , |
|
|
|
(6.2) |
||||||
|
|
|
|
V =Li(V |
|
1 |
|
i |
|
1,i |
) ω |
1 |
)+ q |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
i |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
i |
|
|
i |
|
|
|
|
|
||||||
|
|
|
|
|
ˆ |
|
|
|
|
T |
( ˆ |
|
+ qi eˆ |
|
|
|
ˆ |
|
|
|
, |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
i |
1,i |
= L |
|
|
|
)- r |
|
1,i |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
i |
|
|
|
ri, i |
|
|
|
|
|
|
i |
|
|
i |
|
|
|
|
|
|
|
|
|
||||||||
ˆ |
|
ˆ |
|
-D( |
ˆ |
|
|
) |
ˆ |
-D( |
ωˆ |
|
|
|
)D( ˆ |
|
|
) |
ωˆ |
)+ |
|
|
|
|
||||||||||||||
W =L |
(W |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
i |
i |
|
i |
|
|
|
i 1,i |
|
|
|
εi |
|
|
|
|
|
i 1 |
|
|
|
|
i 1,i |
|
|
i 1 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
+ qi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
1 , |
|
|
|
|
|
(6.3) |
||||||
|
|
|
|
|
|
|
|
|
eˆi -2 qi |
D( eˆi )Li ωi |
|
|
|
|
|
|
||||||||||||||||||||||
где D( |
ˆ |
1,i |
), D( ωˆ i |
1 ), D( eˆi ) – матрицы 3 |
|
3, содержащие ком- |
||||||||||||||||||||||||||||||||
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поненты |
ˆi |
1,i , |
eˆi , ωˆ i |
|
1 , порождаются векторными произведе- |
|||||||||||||||||||||||||||||||||
ниями. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для вращательной i-1,i кинематической пары |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
ˆ |
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
(6.4) |
||||
|
|
|
|
|
|
|
|
ωi |
=Li ωi |
1 + qi |
ei |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
ˆ |
|
|
ˆ |
|
+ D( rˆ |
|
|
|
) |
ωˆ |
|
|
)–D( |
ˆ |
|
) ωˆ |
|
, |
|
|
|
(6.5) |
|||||||||||||||
|
V |
=Li(V |
1 |
|
|
1,i |
|
1 |
|
i |
|
|
|
|||||||||||||||||||||||||
|
i |
|
|
|
i |
|
|
|
|
i |
|
|
|
|
|
i |
|
|
|
|
|
|
ri, i |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
εˆi =Li εˆi |
1 + qi |
eˆi -2 qi D( eˆ i )Li ωˆ i 1 , |
|
|
|
(6.6) |
||||||||||||||||||||||||||||
|
ˆ |
|
|
|
ˆ |
|
|
|
|
|
|
|
ˆ |
|
|
) |
ˆ |
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
ˆ |
|
ˆ |
|
|
)- |
||
|
W |
=Li (W |
|
1 |
+ D( r |
1,i |
ε |
|
1 |
+ D( ω |
1 |
)D( r |
1,i |
) ω |
1 |
|||||||||||||||||||||||
|
i |
|
|
|
i |
|
|
|
|
|
|
|
i |
|
|
|
i |
|
|
|
|
|
|
|
i |
|
i |
|
i |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
79 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

-D( rˆ i,i ) εˆi -D( ωˆ i )D( rˆ i,i ) ωˆ i .
Соотношения (6.8) и (6.9) принимают вид:
|
|
|
|
εˆi = |
i |
|
|
|
|
|
ˆ |
+ Kio |
εˆ0 , |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
ˆij q j + θi |
|
|
|
|||||||||||
|
|
|
|
|
|
j |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
= |
|
i |
ˆ |
|
+ |
ˆ |
|
+ Kio |
ˆ |
, |
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
W |
|
|
i |
W |
|
|
|||||||||||
|
|
|
|
i |
|
|
|
ij |
q j |
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
j |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
где αˆ |
= { α |
k |
|
}, |
|
ˆ |
= { |
k |
}, |
ˆ |
|
= { θ |
k |
}, |
ˆ |
= { |
k }, |
|||
ij |
|
ij |
θ |
i |
||||||||||||||||
ij |
|
|
|
ij |
|
|
|
|
|
i |
|
|
|
i |
|
i |
||||
Kio – матрица преобразования Z0 |
|
Zi. |
|
|
|
|||||||||||||||
(6.7)
(6.8)
(6.9)
Для поступательной i-1,i кинематической пары
|
|
|
|
|
|
αˆ ii =0, |
αˆ |
= Li |
|
ˆ |
|
1, j |
(i |
|
j) |
||||||||
|
|
|
|
|
|
|
ij |
|
αi |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
ˆ |
|
|
ˆ |
ii |
= |
eˆi , |
|
|
||
|
|
|
|
|
|
|
|
θi = Li θi 1 , |
|
|
|
|
|||||||||||
|
|
|
|
|
|
ˆ ij =Li( ˆ i |
1, j -D( ˆ i |
1,i ) αˆ i 1, j ) (i |
j), |
||||||||||||||
ˆ |
|
=Li( |
ˆ |
|
ˆ |
|
|
|
ˆ |
|
|
|
ˆ |
1 )-Li D( |
ˆ |
|
|
ˆ |
|||||
|
i |
|
i |
1 |
-D( ωi 1 )D( |
|
i |
1,i |
) ωi |
i |
1,i |
)( θi 1 + |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
+ Ki-1,0 |
εˆ0 )-2 qi D( eˆi )Li ωˆ i |
1 , |
|
(6.10) |
|||||||||||||
где Ki-1,0 – матрица преобразования Z0 |
|
Zi-1 . |
|
||||||||||||||||||||
|
|
Для вращательной i-1,i кинематической пары |
|||||||||||||||||||||
|
|
|
|
|
|
ˆ |
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
α |
|
|
|
|
|
1, j |
(i |
|
j), |
|
|
, |
|||||
|
|
|
|
|
|
ij |
=Li αi |
|
αˆ ii = ei |
||||||||||||||
|
|
|
|
|
|
ˆ |
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
θi |
=Li θi 1 |
- qi D( eˆi )Li ωi 1 , |
|
||||||||||||||
|
|
|
|
|
|
ˆ |
ii |
= -D( rˆ |
i,i |
) eˆ |
|
, |
|
|
|
|
|
(6.11) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
ˆ ij =Li( ˆ i 1, j -D( ˆ i 1,i ) αˆ i 1, j ) (i |
j) , |
||||||||||||||||
|
|
ˆ |
|
=Li ( ˆi 1 -D( |
|
ˆ |
|
|
|
ˆ |
|
|
|
|
ˆ |
|
|
ˆ |
ˆ |
||||
|
|
|
|
i |
|
|
i |
1,i ) θi |
1 + D( ωi |
1 )D( ri |
1,i ) ωi 1 )– |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-Li D( |
ˆ |
K |
|
ε |
+ |
D( ˆ |
ˆ |
|
ˆ |
|
ˆ |
|
|
ˆ |
|
||
i 1,i |
i-1,0 |
q |
)D( e |
)Li ω |
-D( ω )D( ˆ |
) ω . |
|||||||||||
|
|
|
|
0 |
i |
ri, i |
|
i |
|
i 1 |
|
i |
ri, i |
|
i |
||
Используя эти рекуррентные соотношения, можно определить угловую скорость и ускорение любого звена ММ и линейную скорость и ускорение его центра масс. Определение кинематических характеристик звеньев ММ нужно начинать с базового звена, поскольку его скорости и ускорения, чаще всего, задаются из условий эксплуатации.
4.7.Кинематический синтез ММ
Проектирование структурной и кинематической схем механизма по заданным его свойствам называется синтезом механизма.
Существуют два этапа синтеза механизма. На первом этапе выбирается структурная схема механизма методами структурного синтеза. Первый этап очень важен, поскольку структура механизма во многом определяет свойства механизма и ошибки структурного синтеза оказываются практически неисправимыми на дальнейших этапах проектирования механизма. Структурный синтез производится путем присоединения структурных единиц (структурных групп или входных звеньев) к входным звеньям. При этом используются справочные данные по механизмам, аналогичным проектируемому механизму.
На втором этапе определяются постоянные параметры выбранной кинематической схемы механизма, обеспечивающие заданные свойства механизма. Этот этап обычно начинается с кинематического синтеза, т.е. определения параметров кинематической схемы механизма по заданным его кинематическим свойствам.
Параметрами синтеза механизма называются независимые между собой постоянные параметры кинематической схемы проектируемого механизма. Параметры синтеза механизма, определенные заданием на проектирование, называются вход-
81
ными параметрами, а параметры синтеза, подлежащие определению, называются выходными параметрами синтеза.
При синтезе ММ выходными являются линейные размеры его звеньев, предельные значения обобщенных координат, а также параметров, определяющих взаимное расположение ММ и обслуживаемого им технологического оборудования. Эти параметры определяются, как правило, из решения задач оптимизации, т.е. задач по определению выходных параметров из условий достижения некоторыми функциями параметров синтеза, называемыми целевыми функциями, экстремальных значений. Целевые функции отражают заданные свойства механизма. Целевые функции в теории оптимизации называют также критериями оптимизации.
Существуют общие (глобальные) и частные (локальные)
критерии оптимизации. Общие критерии оптимизации описывают самые общие свойства механизма, проявляющиеся во всей рабочей зоне и при выполнении любых рабочих операций. Такие критерии используются при синтезе универсальных ММ.
К общим критериям оптимизации относятся локальный и полный коэффициенты сервиса, локальная и глобальная мобильность, точность позиционирования схвата, маневренность, коэффициент полезного действия и другие.
Частные критерии учитывают специфические условия и особенности выполнения конкретных производственных операций и используются при синтезе специализированных ММ.
82
5.Инерционные характеристики звена
2.5.в пространственном движении
Произвольное про-
странственное движение звена можно разбить на поступательное движение вместе с полюсом и вращательное движение относительно мгновенной оси, проходящей через полюс. Инерционные свойства звена в поступательном движении вполне определяются массой звена m. Инер-
ционные свойства звена, вращающегося вокруг неподвижной точки, имеют более сложную природу и характеризуются тензором инерции звена. Для определения компонентов тензора инерции нужно рассмотреть вращение звена вокруг неподвижной точки.
Пусть в звене (рис. 5.1) в окрестности точки А, заданной вектор - радиусом r , выделен элемент с объемом dV и массой
dm= dV ,
dV ,
где  - плотность материала звена в окрестности точки А, за-
- плотность материала звена в окрестности точки А, за-
висящая в общем случае от положения точки А относительно звена.
По определению, масса звена
m= d m = dV . v v
При постоянной плотности m= V , где V – объем, занятый звеном.
V , где V – объем, занятый звеном.
83
|
o |
~ |
Пусть |
Z |
- неподвижная система отсчета, а Z - система |
отсчета, связанная с звеном. Пусть положение начала отсчета
~ |
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и точка |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
системы Z в системе |
Z задано вектор – радиусом |
S |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S – центр масс звена. Тогда для точки А (рис. 5.1) |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
S + |
|
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
= |
|
r |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Статическим моментом инерции звена относительно точки |
|||||||||||||||||||||||||||
О называется вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
dm = |
|
dV = ( |
|
|
|
|
|
)dV = |
|
|
|||||||||||||
S0 = |
|
|
|
S |
|
|
|
||||||||||||||||||||
|
|
|
|
r |
|
|
|||||||||||||||||||||
|
|
v |
|
|
|
v |
|
|
|
|
v |
|
|
||||||||||||||
|
|
|
|
|
= |
|
S v dV + |
|
dV . |
|
|
||||||||||||||||
|
|
|
|
|
|
r |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|||||||||||||
Но |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
dV =m, |
|
|
|
dV = Ss - |
|
|
||||||||||||||||
|
|
|
|
|
|
r |
|
|
|||||||||||||||||||
|
|
|
|
v |
v |
|
|
||||||||||||||||||||
статический момент звена относительно точки S.
Центром масс называется точка звена, относительно которой статический момент звена равен нулю.
Поскольку точка S -центр масс, Ss =0 и S0 =m S . Отсюда
следует, что вектор - радиус |
|
|
центра масс S звена относи- |
|
S |
||||
|
|
|||
тельно некоторой точки О равен отношению статического момента относительно этой точки к массе звена
|
|
|
|
|
|
S = S0 /m |
(2.1) |
||
|
||||
Условие Ss =0 эквивалентно трем скалярным условиям:
~ k
r dV =0 (k =1,2,3).
v
Если 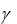 = const, то
= const, то
84
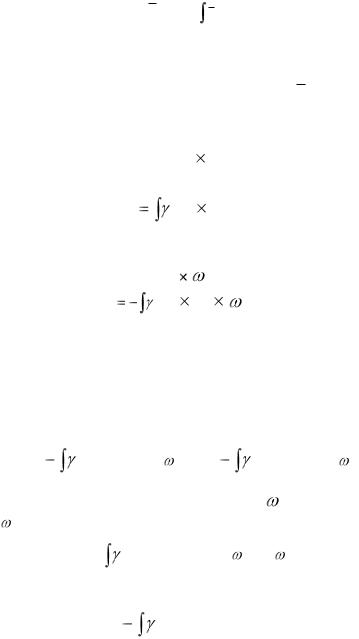
Ss = 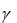 r dV .
r dV .
v
~
Система координат Z называется центральной, если еѐ оси проходят через центр масс звена. Тело, ограниченное объемом
dV, можно считать материальной точкой. Если V - вектор скорости точки А, то момент импульса материальной точки А относительно центра масс звена S определяется вектором
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
ls =dm( |
|
|
|
|
|
|
|
V ). |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
r |
|
|
|
|
|
|||||||||||||||||||||
Вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
Ls |
|
|
|
|
|
( |
|
|
|
|
|
V )dV |
|
|
|
|||||||||||||
|
|
|
|
|
|
r |
|
|
(2.2) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
называется моментом импульса звена относительно точки S. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
По формуле Эйлера V = - |
r |
|
|
|
|
|
( |
|
|
|
и |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Ls |
|
|
|
|
|
( |
r |
|
|
|
|
|
r |
|
|
|
|
))dV. |
(2.3) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
Проекции Ls на оси связанной с звеном системы |
|||||||||||||||||||||||||||||||||
Z опре- |
|||||||||||||||||||||||||||||||||
деляется матрицей - столбцом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
~ |
|
|
|
~ k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
ˆ |
|
} (k = 1,2,3). |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
Ls ={ Ls |
|
|
|
|||||||||||||||||||||||
С учетом ранее введенных обозначений |
|
|
|
||||||||||||||||||||||||||||||
~ |
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|||||
ˆ |
|
|
|
|
|
|
|
|
|
|
))dV= |
|
|
|
|
||||||||||||||||||
Ls = |
|
|
(D( rˆ )(D( rˆ ) ˆ |
(D( rˆ )(D( rˆ ) ˆ dV. |
|||||||||||||||||||||||||||||
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
||||||
|
|
|
|||||||||||||||||||||||||||||||
Поскольку для всех точек звена вектор |
|
|
, а значит и мат- |
||||||||||||||||||||||||||||||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рица ˆ одинаковы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
~ |
~ |
|
|||||||||||
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.4) |
||||||||||||||||||
|
Ls =-( |
(D( rˆ )(D( rˆ )dV) ˆ |
= J |
ˆ , |
|||||||||||||||||||||||||||||
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
(D( rˆ )(D( rˆ )dV - |
|
|
|
||||||||||||||||||||||
|
|
|
J = |
|
|
|
|
|
|
|
(2.5) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
85 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
