
Учебное пособие 1691
.pdf
y
y = f (x)
 M(x0; y0 )
M(x0; y0 )
 α
α
х
Рис. 2.3. Касательная и нормаль к кривой
Нормалью к кривой называется прямая, которая перпендикулярна касательной в точке касания.
Так как нормаль перпендикулярна касательной, то ее угловой коэффициент будет равен
k |
|
= − |
1 |
= − |
1 |
(если f ′(x |
)≠ 0 ). |
норм |
|
f ′(x0 ) |
|||||
|
|
kкас |
|
0 |
|
||
|
|
|
|
|
|
Поэтому уравнение нормали примет вид:
y − y = − |
1 |
|
(x − x |
) |
. |
(2.10) |
|
f ′(x |
) |
||||||
0 |
0 |
|
|
|
|||
|
0 |
|
|
|
|
|
2.5. Механический смысл производной
Рассмотрим прямолинейное неравномерное движение материальной точ-
ки. Пусть материальная точка М движется по прямой. За время t точка прошла расстояние OM = S (рис. 2.4). Это расстояние зависит от истекшего времени t, т.е. путь есть функция от времени
S = S (t ). |
(2.11) |
Равенство (2.11) называется законом движения точки.
71

О |
М M1 |
S (t ) |
S |
|
|
|
S |
S (t + |
t ) |
Рис. 2.4. Прямолинейное движение материальной точки
За время t ( t – приращение времени) точка пройдет путь от точки М до точки M1:
MM1 = S(t + t) − S(t) = S ,
где S – приращение пути.
Если бы движение было равномерным, то точка бы двигалась с постоян-
ной скоростью V = |
S |
. При неравномерном движении скорость в каждый мо- |
|
t |
|||
|
|
мент времени меняется и в этом случае вводят понятие мгновенной скорости движения или скорости в данный момент, т.е. V =V (t ):
V (t )= lim |
S |
= lim |
S (t + |
t )− S (t ) |
= S′(t ). |
(2.12) |
t |
|
t |
||||
t→0 |
t→0 |
|
|
|||
Формула (2.12) справедлива и для равномерного движения.
Итак, механический смысл производной состоит в том, что скорость есть производной пути по времени.
2.6. Производные высших порядков
Производная y′ = f ′(x) функции y = f (x) есть также функция от х и на-
зывается производной первого порядка.
Если функция f ′(x) дифференцируема, то ее производная называется производной второго порядка и обозначается y′′ или f ′′(x). Таким образом y′′ =(y′)′.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается y′′′ или f ′′′(x). Сле-
72

довательно, y′′′ =(y′′)′. |
|
|
Производной n –го порядка |
называется производная от |
производной |
(n −1)–го порядка (если все (n −1) |
производная функции y = f |
(x) существу- |
ют), т.е. |
|
|
y(n) =(y(n−1) )′.
Производные порядка выше первого называются производными высших порядков.
Замечание 2.1. Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках. Например, yVI или y(6)
– производные шестого порядка.
2.7. Дифференциал функции
Дифференциалом функции y = f (x) называется произведение производ-
ной функции f ′(x) на приращение независимой переменной |
x и обозначается |
dy = f ′(x) x или d f (x)= f ′(x) x . |
(2.13) |
Рассмотрим функцию y = x . Применяя формулу (2.13), найдем ее диффе-
ренциал |
|
′ |
x . |
dy = dx = x x =1 |
Следовательно, дифференциал независимой переменной и приращение независимой переменной совпадают, поэтому формулу дифференциала (2.13)
записывают в виде: |
|
|
|
|
|
|
|
|
|
|
|
. |
(2.14) |
||
|
dy = f ′(x)d x |
||||||
Из равенства (2.14) следует, что производная функции равна отношению |
|||||||
дифференциалов dy и d x |
|
|
|
|
|
|
|
|
|
′ |
|
dy |
|
|
|
|
f |
(x)= d x . |
|
||||
|
|
|
|||||
Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточ-
73

ного аргумента, т.е.
dy = yu′du .
Пример 2.5. Найти дифференциал функции |
y = |
|
|
1 |
|
. |
|
|
|
|||||||||||||||||
|
|
+ x2 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||
Решение. Для нахождения дифференциала применим формулу (2.13). |
||||||||||||||||||||||||||
Сначала вычислим производную функции |
y = |
|
|
1 |
|
|
: |
|
|
|
|
|
|
|
|
|||||||||||
|
|
+ x2 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
′ |
|
1 |
|
|
|
|
|
′ |
|
|
|
|
|
|
2x |
|
|
|
|
|||
y′ = |
|
|
|
|
|
= − |
|
|
(1+ x2 ) |
= − |
|
|
|
|
|
|
, |
|||||||||
|
+ x |
2 |
(1+ x2 ) |
2 |
(1 + x2 ) |
2 |
||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
а потом подставим ее в равенство (2.13) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
dy = − |
|
|
2x |
|
|
|
d x |
|
|
1 |
|
|
|
|
|
|
|
|
|
2x |
|
d x . |
||||
|
|
|
|
|
|
или d |
|
|
|
= − |
|
|
|
|
|
|
|
|||||||||
(1+ x2 )2 |
|
|
|
|
(1+ x2 )2 |
|||||||||||||||||||||
|
|
|
1+ x2 |
|
|
|
|
|
|
|
||||||||||||||||
В соответствии с таблицей производных (см. табл. 2.1), напишем таблицу дифференциалов (табл. 2.2).
№
1
2
3
4
5
6
7
8
Таблица 2.2
Функция |
Дифференциал |
||||||||
y = const |
dy = 0 |
||||||||
Степенная |
функция и ее частные случаи |
||||||||
y = xn |
dy = nxn−1 d x |
||||||||
y = x |
dy = d x |
||||||||
y = |
x |
dy = |
|
1 |
|
d x |
|||
|
|
2 |
|
x |
|||||
y = |
1 |
dy = − |
|
1 |
d x |
||||
x |
|
|
|||||||
|
|
|
|
|
x2 |
||||
Показательная |
функция и ее частный случай |
||||||||
y = ax |
dy = ax ln a dx |
||||||||
y = ex |
dy = ex dx |
||||||||
Логарифмическая |
функция и ее частный случай |
||||||||
y = loga x |
dy = |
|
|
1 |
|
|
dx |
||
|
|
xln a |
|||||||
74

№
9
10
11
12
13
14
15
16
17
|
|
|
|
|
|
|
|
|
Окончание табл. 2.2 |
|||
Функция |
|
Дифференциал |
||||||||||
y = ln x |
|
dy = |
1 dx |
|
|
|||||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
Тригонометрические функции |
|
|
|
|
||||||||
y =sin x |
|
dy = cos x dx |
||||||||||
y = cos x |
|
dy = −sin x dx |
||||||||||
y = tg x |
|
dy = |
|
|
|
|
|
1 |
d x |
|||
|
|
|
|
|
|
|
||||||
y = ctg x |
|
cos2 x |
||||||||||
|
|
|
|
|
|
|||||||
|
dy = − |
|
|
1 |
|
dx |
||||||
|
|
|
|
|
||||||||
|
|
sin2 x |
||||||||||
|
|
|
|
|
|
|
|
|
||||
Обратные |
|
тригонометрические функции |
||||||||||
y = arcsin x |
|
dy = |
|
|
|
|
|
|
1 |
|
dx |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||
y = arccos x |
|
|
|
1− x2 |
||||||||
|
|
|
|
|
|
|
||||||
|
dy = − |
|
|
|
|
1 |
|
|
dx |
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
y = arctg x |
|
|
|
|
|
|
|
1− x2 |
||||
|
dy = |
|
|
|
1 |
dx |
||||||
|
|
|
|
|||||||||
|
|
|
|
|
||||||||
y = arcctg x |
|
|
|
|
1 + x2 |
|
|
|
||||
|
dy = − |
|
1 |
|
dx |
|||||||
|
|
|
|
|||||||||
|
|
|
+ x2 |
|||||||||
|
|
1 |
|
|
||||||||
2.8. Признаки постоянства, возрастания и убывания функции
Если производная функции в каждой точке некоторого интервала (a;b) равна нулю, то функция будет постоянной в каждой точке этого интервала, т.е.
y′ = 0 y =C для всех x (a;b).
Функция y = f (x) называется возрастающей (убывающей) на некотором интервале (a;b), если на этом интервале большему значению аргумента соответствует большее (меньшее) значение функции, т.е. для x1, x2 (a;b),
если x2 > x1 и f (x2 )> f (x1 ), то y = f (x) – возрастающая функция; если x2 > x1 и f (x2 )< f (x1 ), то y = f (x) – убывающая функция.
Теорема 2.1 (достаточное условие возрастания и убывания функции).
Если функция y = f (x) дифференцируема на некотором интервале (a;b) и
75
производная функции положительна f ′(x) > 0 (отрицательна f ′(x)< 0 ) для всех x (a;b), то функция будет возрастающей (убывающей) на этом интерва-
ле.
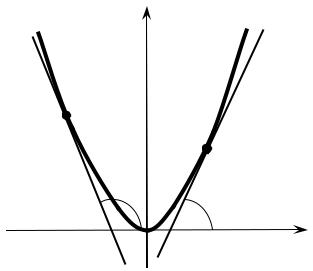
Пример 2.6. Найти интервалы возрастания и убывания функции y = x2 . |
|
||||||||||
Решение. Производная функции y = x2 |
равна y′ = 2x . |
|
|
|
y′ > 0 |
|
|||||
у |
y = x2 |
|
Если |
x > 0 , |
то |
|
|||||
|
|
функция |
y = x |
2 |
возрастает на |
||||||
|
|
|
|
||||||||
|
|
|
интервале (0;∞). |
|
|
|
|||||
|
|
|
Если |
|
же |
|
|
x < 0 , |
то |
||
|
|
|
y′< 0 |
|
функция |
y = x2 |
|||||
|
|
|
убывает на интервале (−∞;0). |
||||||||
α |
α |
|
Из геометрического смыс- |
||||||||
|
|
ла производной следует, что |
|||||||||
|
|
|
|||||||||
О |
|
х |
если |
касательная |
составляет |
||||||
|
|
|
острый угол с осью Ox , то |
||||||||
Рис. 2.5. Чертеж к примеру 2.6. |
|
функция возрастает, а если |
|||||||||
|
тупой, то |
функция |
убывает |
||||||||
|
|
|
(рис. 2.5). |
|
|
|
|
|
|
|
|
2.9. Экстремумы функции
Пусть точка x = x0 лежит внутри области определения функции y = f (x). Точка x = x0 называется точкой максимума функции y = f (x), если в некоторой окрестности точки x0 для всех x ≠ x0 из этой окрестности выполня-
ется неравенство f (x)< f (x0 ).
Точка x = x0 называется точкой минимума функции y = f (x), если в некоторой окрестности точки x0 для всех x ≠ x0 из этой окрестности выполняется
неравенство f (x)> f (x0 ).
Значение функции f (x0 ) в точке максимума (минимума) называется
максимумом (минимумом) функции (рис. 2.6 и 2.7).
Максимумы и минимумы функции называются экстремумами функции. Экстремумы функции имеют локальный характер: отдельные минимумы
могут быть больше отдельных максимумов той же функции (рис. 2.8).
76

у
max f (x)= f (x0 ) 
 f (x)
f (x)
y = f (x)
х |
x0 |
х |
Рис. 2.6. Максимум функции y = f (x)
у
y = f (x)
f (x)
min f (x)= f (x0 )
x0 х х
Рис. 2.7. Минимум функции y = f (x)
у
y = f (x)
О min |
max |
х |
Рис. 2.8. Локальный характер экстремумов
77

Теорема 2.2 (необходимое условие существования экстремума). Если дифференцируемая функция y = f (x) имеет экстремум в точке x = x0 , то ее
производная равна нулю в этой точке:
f ′(x |
)= 0 . |
(2.14) |
0 |
|
|
Геометрически равенство (2.14) означает, что если x0 точка экстремума, то касательная к графику дифференцируемой функции y = f (x) в точке (x0; f (x0 )) параллельна оси Ox (рис. 2.9).
у
y = f (x)
x0 |
|
х |
|
Рис. 2.9. Геометрическая интерпретация равенства (2.14) |
|
||
Отметим, что обратное утвержде- |
|||
ние (если |
f ′(x |
)= 0 , то x = x |
– точка |
|
0 |
0 |
|
экстремума) неверно. Например, для |
|||
функции |
y = x3 |
ее производная |
y′ =3x2 |
равна нулю при x = 0 , но x = 0 не является точкой экстремума (рис. 2.10).
Есть функции, у которых в точках экстремума производная не существует. Такими точками являются угловые точки и точки, в которых производная обращается
в бесконечность. Например, |
функция |
||||
y = |
|
x |
|
(рис. 2.11) в точке x = 0 |
производ- |
|
|
||||
ной не имеет (касательная в точке O(0;0)
Рис. 2.10. График функции y = x3 не существует), но x = 0 – точка минимума функции y = x .
78

Рис. 2.11. График функции y = x
Функция y = 3 x2 , график которой изображен на рис. 2.12, в точке O(0;0)
имеет экстремум (минимум), однако в этой точке производная не существует, так как в точке O(0;0) касательная не имеет углового коэффициента.
у
y = f (x)
Ох
Рис. 2.12. График функции y = 3 x2
Точка, в которой производная функции равна нулю, называется стацио-
нарной точкой. Стационарные точки, а также точки, в которых производная не существует или бесконечна, называются критическими.
Точки экстремума следует искать именно среди критических точек.
Теорема 2.3 (достаточное условие существования экстремума). Если функция y = f (x) дифференцируема в некотором интервале, содержащем кри-
тическую точку x0 , кроме, быть может, самой точки x0 , и при переходе через нее слева направо производная f ′(x) меняет знак с плюса на минус, то x0
есть точка максимума; если же производная f ′(x) меняет знак с минуса на плюс, то x0 есть точка минимума.
79

у
max f (x)= f (x0 ) 
f ′(x0 )> 0 |
f ′(x |
)< 0 |
|
0 |
|
x0 |
|
х |
у
f |
′ |
(x |
)< 0 |
f ′(x |
)> 0 |
|
0 |
|
|||
|
|
0 |
|
|
|
min f (x)= f (x0 )
x0 |
х |
Рис. 2.13. Геометрическая интерпретация теоремы 2.3.
2.9. Наибольшее и наименьшее значения функции на отрезке
Наибольшее и наименьшее значения функции y = f (x), заданной на отрезке [a;b], называются глобальными экстремумами на этом отрезке.
Нахождение глобальных экстремумов проводят по следующей схеме:
1. Находят критические точки функцию, принадлежащие интервалу
(a;b).
2.Вычисляют значение функции на границах отрезка [a;b] и в критиче-
ских точках, принадлежащих интервалу (a;b).
80
