
Учебное пособие 1691
.pdf
Пример 1.2. Составить уравнение стороны ВС треугольника АВС, если известны координаты его вершин: A(1;2), B(−2;3) и C (2;−5). Определить ко-
ординаты направляющего S и нормального N векторов прямой ВС. Решение. Так как известны координаты двух точек, через которые про-
ходит прямая ВС, то воспользуемся уравнением (1.19):
x −(−2) |
= |
y −3 |
|
|
|
. |
|
2 −(−2) |
−5 −3 |
||
Складывая числа в знаменателях дробей, получим каноническое уравнение прямой:
x +4 2 = y−−83 ,
из которого найдем координаты направляющего вектора прямой – S {4;−8}. Координаты нормального вектора N {A; B} можно определить из общего уравнения прямой, которое получим из канонического:
x + 2 |
= |
y −3 |
−2 (x + 2)=1 (y −3) 8x + 4 y + 4 = 0 или |
|
4 |
−8 |
|||
|
|
2x + y +1 = 0 .
Таким образом, координаты нормального вектора прямой – N {2;1}.
Уравнение прямой в отрезках
Пусть прямая не проходит через начало координат и пересекает ось Oy в точке M1 (0;b), а ось Ox – в точке M2 (a;0) (рис. 1.19).
|
y |
L |
M1 (0; b) |
|
b
M2 (а; 0)
0 |
x |
а
Рис. 1.19. Вывод уравнения прямой в отрезках
21

В этом случае уравнение (1.19) примет вид |
|
|
|
|
|
|
|||||||||
|
x −0 |
|
y −b |
|
x |
|
y −b |
|
|
|
|
|
|
|
|
|
= |
или |
= |
|
|
x |
+ |
y |
=1 |
. |
(1.20) |
||||
|
a −0 |
0 −b |
a |
−b |
a |
b |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
Это уравнение называется уравнением прямой в отрезках, так как числа a и b указывают, какие отрезки (с учетом знака) отсекает прямая на осях координат (см. рис. 1.19).
Уравнение прямой с угловым коэффициентом
Пусть прямая непараллельна оси OY . Тогда первая координата направляющего вектора S {m;n} не равна нулю ( m ≠ 0 ). Каноническое уравнение (1.18) перепишем в следующем виде:
|
|
|
y − y = |
n |
(x − x |
), |
|
|||
|
|
|
|
|||||||
|
|
0 |
|
m |
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
||
или, обозначив величину |
n |
через k, получим |
|
|
|
|
||||
m |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
y − y0 |
= k (x − x0 ) |
|
, |
(1.21) |
|||
где k = tgϕ – тангенс угла, который составляет прямая c положительным направлением оси Ox (рис. 1.20).
y |
L |
S {m; n} |
|
ϕ n |
ϕ |
m |
b |
|
|
0 |
x |
Рис. 1.20. Вывод уравнения прямой с угловым коэффициентом
Величина k = tgϕ называется угловым коэффициентом прямой, а
уравнение (1.21) – уравнением прямой, проходящей через данную точку в
данном направлении.
22

Рассмотрим частный случай уравнения (1.21), в котором в качестве точки M0 возьмем точку M (0;b) пересечения прямой с осью Oy . Подставим коор-
динаты этой точки в (1.21): y −b = k (x −0) или
y = kx +b |
, |
(1.22) |
где b – отрезок, отсекаемый прямой на оси Oy (см. рис 1.20).
Уравнение (1.22) называется уравнением прямой с угловым коэффициентом.
Заметим, что к виду (1.22) можно привести уравнение любой прямой непараллельной оси Oy .
1.2.2. Расстояние от точки до прямой
Пусть заданы прямая L общим уравнением Ax + By +C = 0 и точка
M0 (x0; y0 ) |
(рис. 1.21). Расстояние d от точки M0 до прямой L (см. рис. 1.21) |
|||||||||||||||||||||||||||||||||
равно модулю проекции вектора |
|
, где M1 (x1; y1 ) |
– произвольная точка |
|||||||||||||||||||||||||||||||
M1M0 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{A; B}. Следовательно, |
||||||||||||||||||
прямой L, на направление нормального вектора N |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
(x0 |
− x1 )A +(y0 |
− y1 )B |
|
|
|
|
|
Ax + By |
− Ax |
− By |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
M M |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
d = |
Пр |
n |
M M |
0 |
|
= |
|
|
1 0 |
|
|
|
= |
|
|
|
|
|
|
|
= |
|
|
0 |
0 |
1 |
1 |
|
|
.(1.23) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
1 |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
A2 + B2 |
|
|
|
|
|
|
|
A2 + B2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
y |
M 1 |
|
|
|
M 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n {A; B} |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
npn M 1M 0 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|||
Рис. 1.21. Расстояние от точки до прямой
Так как точка M1 (x1; y1 ) принадлежит прямой L, то ее координаты удовлетворяют ее уравнению, т.е. Ax1 + By1 +C = 0 . Откуда имеем
C = −Ax1 − By1 . |
(1.24) |
23

Подставляя (1.24) в выражение (1.23), получим формулу
d = Ax0 + By0 +C . |
(1.25) |
A2 + B2 |
|
Пример 1.3. Используя условие примера 1.2 (см. стр. 21), найти площадь треугольника АВС.
Решение. Известно, что площадь треугольника равна половине произведения длины его стороны а на длину высоты h, опущенной на сторону а:
S = 12 a h .
Проведем высоту в треугольнике АВС, например, из вершины А на сторону ВС. Так как нам известны координаты точек В и С, то длину стороны ВС будет искать по формуле
a = BC = (xc − xb )2 +(yc − yb )2 = (2 −(−2))2 +(−5 −3)2 = 80 = 4 5 .
Длину высоты h можно найти как расстояние от точки А до стороны ВС. Уравнение прямой ВС было составлено в примере 1.2:
|
|
|
|
|
|
|
2x + y +1 = 0 |
, |
|
|
|||||
поэтому, пользуясь формулой (1.25), получим |
|
|
|
||||||||||||
|
|
h |
|
= |
|
|
2 1+1 2 +1 |
|
|
= |
|
|
5 |
= |
5 . |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
5 |
|||||
|
|
|
|
22 +12 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||||||||
Итак, площадь треугольника АВС равна |
|
|
|
||||||||||||
|
|
S = 1 4 5 5 = |
10 кв.ед. |
||||||||||||
2 |
|
|
|
|
|
|
|
|
|||||||
24

1.2.3. Угол между двумя прямыми.
Условия параллельности и ортогональности двух прямых
Пусть прямые L1 и L2 заданы уравнениями с угловыми коэффициентами
y = k1x +b1 и y = k2 x +b2 (рис. 1.22). Углом между двумя прямыми L1 и L2 называется угол α , на который нужно повернуть вокруг точки пересечения против часовой стрелки прямую L1 до совмещения с прямой L2 .
y |
L2 |
L1 |
|
|
α |
|
ϕ1 |
ϕ2 |
0 |
|
х |
Рис. 1.22. Угол между прямыми
По теореме о внешнем угле треугольника имеем ϕ2 =α +ϕ1 или
α =ϕ |
2 |
−ϕ . Если α ≠ π |
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tgϕ2 − tgϕ1 |
|
|
|||||||
|
|
|
|
tgα = tg(ϕ |
2 |
−ϕ )= |
. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
1 |
|
|
1+ tgϕ2 |
tgϕ1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Так как tgϕ1 = k1 и tgϕ2 = k2 получим |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
tgα = |
|
|
k2 − k1 |
|
|
. |
|
(1.26) |
||||||
|
|
|
|
|
1 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
+ k |
2 |
k |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Если прямые L1 и L2 параллельны, то α = 0 и tgα = 0 . Из формулы (1.26) |
|||||||||||||||||||
следует k2 − k1 = 0 , т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
k2 = k1 |
. |
|
|
|
|
|
(1.27) |
|||||
Таким образом, условием параллельности двух прямых является равенство их угловых коэффициентов.
Если же прямые L1 и L2 ортогональны, то α = π2 . Следовательно,
25
ctgα = |
1+ k2 k1 |
= 0 |
1+ k |
2 |
k |
= 0 , т.е. |
|
|||||
|
|
|
||||||||||
|
k2 − k1 |
|
1 |
|
|
|||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
или |
k = − |
1 |
|
. |
(1.28) |
|
|
|
k |
2 |
k = −1 |
||||||||
|
|
|
||||||||||
|
|
|
1 |
|
|
1 |
|
k2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, у ортогональных прямых угловые коэффициенты обратны по величине и противоположны по знаку.
Пример 1.4. Используя условие примера 1.2, составить уравнение высоты h треугольника АВС, проведенной из вершины А на сторону ВС и найти угол между этой высотой и стороной АС.
Решение. Уравнение прямой ВС нам известно (см. пример 1.2):
2x + y +1 = 0 .
Перепишем его в виде (1.22):
y = −2x −1.
Откуда видно, что угловой коэффициент прямой ВС равен
kBC = −2.
Так как угловые коэффициенты у ортогональных прямых (h и ВС) удовлетворяют равенству (1.28), то
kh = − |
1 |
= − |
1 |
= |
1 . |
|
−2 |
||||
|
kBC |
|
2 |
||
Используя уравнение прямой, проходящей через данную точку в данном направлении (1.21), составим уравнение высоты h:
y − 2 = |
1 |
(x −1) или x − 2 y +3 = 0 . |
|
2 |
|
Угол между высотой h и стороной АС можно найти по формуле (1.26). Определим угловые коэффициенты высоты h и прямой АС. Угловой коэффици-
26
ент высоты h найден ранее ( kh = 12 ).
Для нахождения углового коэффициента прямой АС составим ее уравнение, воспользовавшись уравнением прямой проходящей через две точки (1.19):
x −1 |
= |
y − 2 |
|
|
x −1 |
= |
y −2 |
|
−7(x −1)=1 (y − 2) y = −7x +9 . |
|||||||||||||
|
−5 − 2 |
|
|
1 |
|
|
−7 |
|
||||||||||||||
2 −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Таким образом, |
|
|
|
|
|
|
|
kAC = −7 . |
|
|||||||||||||
Итак |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
15 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
tgα = |
|
|
kAC − kh |
|
= |
|
|
−7 − 2 |
|
= |
− |
|
2 |
=3 |
α = arctg 3 ≈ 71,57°. |
|||||||
1 |
+ kAC |
kh |
|
|
|
|
|
|
1 |
|
|
5 |
||||||||||
|
|
|
|
1+(−7) |
|
− |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
||||||||
1.2.4. Кривые второго порядка
Общий вид уравнения второго порядка в заданной прямоугольной системе координат следующий:
Ax2 + Bxy +Cy2 + Dx + Ey + F = 0 ,
причем среди коэффициентов А, В или С должен быть хотя бы один ненулевой. Кривыми второго порядка являются: окружность, эллипс, гипербола и
парабола.
В этом параграфе рассмотрим уравнение, в котором отсутствует произведение переменных, т.е. B = 0:
Ax2 +Cy2 + Dx + Ey + F = 0 .
Такое уравнение задает либо кривую второго порядка, либо пару прямых, либо точку, либо пустое множество.
Окружность
Окружностью называется геометрическое место точек на плоскости, равноудаленных от фиксированной точки, называемой центром окружности.
27
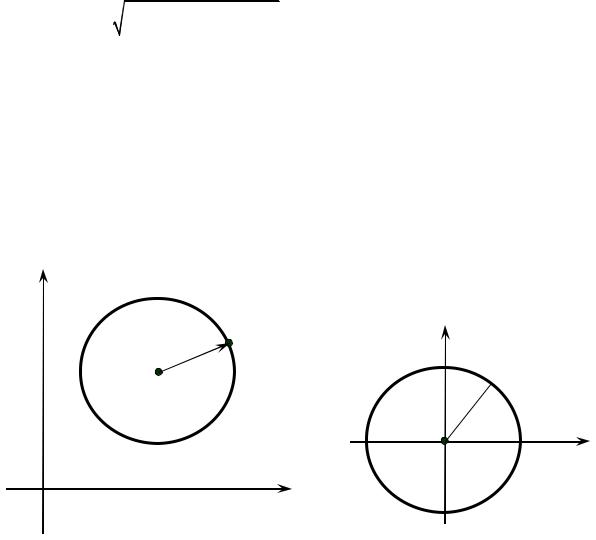
|
|
|
Пусть центром окружности является точка |
M0 (x0; y0 ), а радиус равен |
|||||||||
R = |
|
|
|
|
|
, где M (x; y) |
– произвольная точка окружности (рис. 1.23). Тогда по |
||||||
|
M0M |
|
|||||||||||
формуле (1.9) имеем |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
R = (x − x )2 |
+(y − y )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(x − x )2 |
+(y − y )2 = R2 |
(1.29) |
||||
0 |
0 |
|
0 |
0 |
|
||||||||
|
|
|
Уравнение (1.29) называется уравнением окружности с радиусом R и |
||||||||||
центром в точке M0 (x0; y0 ). |
|
|
|
|
|
||||||||
|
|
|
Частным случаем уравнения (1.29) является уравнение |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x2 + y2 = R2 |
, |
|
(1.30) |
||
описывающее окружность с центром в начале координат (рис. 1.24).
у
M0 |
M |
у |
|
R |
|
||
|
|
|
|
|
|
|
R |
|
|
|
х |
0 |
|
х |
|
Рис. 1.23. Окружность с центром в |
Рис. 1.24. Окружность с центром |
||
точке M0 |
(x0; y0 ) |
в начале координат |
|
Эллипс
Эллипсом называется геометрическое место точек на плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2 , назы-
ваемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.
28

Если выбрать систему координат, у которой начало расположено в середине отрезка F1F2 и ось OX сонаправлена вектору OF2 , то уравнение эллипса имеет вид
|
x2 |
+ |
y2 |
=1 |
, |
(1.31) |
|
a2 |
b2 |
||||
|
|
|
|
|
где а и b – большая и малая полуоси эллипса соответственно.
Уравнение (1.31) называется каноническим уравнением эллипса.
Исследуем форму эллипса, пользуясь его каноническим уравнением.
1. Отметим, что координаты x и y входят в уравнение (1.31) только в четных степенях. Поэтому, если точка(x; y) принадлежит эллипсу, то ему также
принадлежат точки (x;−y), (−x; y) и (−x;−y). Таким образом, эллипс – кривая, которая симметрична относительно осей Ox и Oy , а также относительно точки O(0;0), которую называют центром эллипса.
2.Найдем точки пересечения эллипса с осями координат. Положив y = 0
вуравнении (1.31), находим две точки A1 (−a;0) и A2 (a;0), в которых ось Ox
пересекает эллипс (рис. 1.25). Положив x = 0 , находим точки пересечения эллипса с осью Oy : B1 (0;−b) и B2 (0;b). Точки A1, A2 , B1 и B2 называются вер-
шинами эллипса. Отрезки A1A2 и B1B2 , а также их длины 2а и 2b называются
соответственно большой и малой осями эллипса.
3. Из уравнения (1.31) следует, что каждое слагаемое в левой части не
превосходит единицы, т.е. имеют место неравенства |
x2 |
≤1 и |
y2 |
≤1 или |
|
a2 |
b2 |
||||
|
|
|
−a ≤ x ≤ a и −b ≤ y ≤b . Таким образом, все точки эллипса лежат внутри прямоугольника, образованного прямыми x = ±a и y = ±b.
4. В уравнении (1.31) сумма неотрицательных слагаемых |
x2 |
и |
y2 |
равна |
|
a2 |
b2 |
||||
|
|
|
единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т.е. если x возрастает, то y уменьшается и наоборот.
Из выше сказанного следует, что эллипс имеет форму, изображенную на рис. 1.25
На рис. 1.25 фокусы эллипса обозначены через F1 и F2 , расстояние между которыми равно 2с, где
c = a2 −b2
29

называется фокусным расстоянием. |
|
|
|
|
||||
|
|
|
|
у |
|
|
|
|
|
|
|
|
B2 |
(0;b) |
|
|
|
|
|
|
|
|
M (x; y) |
|
|
|
|
|
|
|
r1 |
r2 |
|
|
|
|
|
|
|
|
|
|
|
|
A |
(−a;0) |
F |
(−c;0) |
0 |
F |
(c;0) |
A |
(a;0) х |
1 |
|
1 |
|
|
2 |
|
2 |
|
B1 (0;−b)
Рис. 1.25. Эллипс
Пусть M (x; y) – произвольная точка эллипса (см. рис. 1.25). Длины отрезков F1M = r1 и F2M = r2 называются фокальными радиусами точки M (x; y). Из определения эллипса следует, что
r1 + r2 = 2a > 2c .
Форма эллипса зависит от отношения ba . Если ba =1, т.е. a =b , то из
(1.31) следует x2 + y2 = a2 – уравнение окружности с центром в точке O(0;0). Таким образом, окружность является частным случаем эллипса, у которого фо-
кусы F и F совпадают (точка О). |
|
|
|
|||
1 |
2 |
|
|
|
|
|
В качестве характеристики формы эллипса чаще используется отношение |
||||||
|
|
|
|
|
|
|
|
|
|
c |
=ε |
, |
(1.32) |
|
|
|
a |
|||
|
|
|
|
|
|
|
называемое эксцентриситетом эллипса, причем 0 ≤ε <1, так как 0 < c < a .
Чем больше величина ε , тем больше форма эллипса отличается от формы
30
