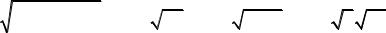
k = |
2 + (−2)2 − 4 2 |
= 2 + −4 = 2 + −1 4 = 2 + 4 −1 = 2 + 2i =1+i . |
|
1 |
2 |
2 |
2 |
2 |
2 |
|
Как известно, если квадратный трехчлен с действительными коэффициентами имеет комплексный корень k1 =α +iβ , то он имеет и сопряженный ко-
рень k2 =α −iβ . Поэтому второй корень характеристического уравнения мож-
но не вычислять, а написать сразу
k2 =1−i .
Корни характеристического уравнения получились комплексные. Значит, по формуле (4.42) получаем общее решение данного ЛОДУ
y = eαx (C1 cos βx +C2 sin βx)= ex (C1 cos x +C2 sin x).
Таким образом, нахождение общего решения ЛОДУ второго порядка с постоянными коэффициентами (4.37) сводится к нахождению корней характеристического уравнения (4.39) и использованию формул (4.40), (4.41), (4.42) общего решения уравнения (не прибегая к вычислению интегралов).
4.4.4. Исследование дифференциального уравнения свободных колебаний
Ранее, в п. 4.2, было выведено уравнение свободных колебаний (4.3):
y′′(t )+ 2λy′(t )+ω2 y(t )= 0 .
ДУ (4.3) является линейным однородным дифференциальным уравнени-
ем второго порядка. Найдем решение этого уравнения. |
|
I. Предположим, что отсутствует сила трения, т.е. μ = 0 |
λ = 0 . Та- |
ким образом, уравнение (4.3) принимает вид |
|
y′′(t )+ω2 y(t )= 0 . |
(4.43) |
Для решения ДУ (4.43) составим характеристическое уравнение
p2 +ω2 = 0 .
Его корнями являются комплексные числа p1 =iω и p2 = −iω . Следовательно, применяя формулу (4.42), получим решение ДУ (4.43)
y =C1 cosωt +C2 sinωt , |
(4.44) |
где C1 и C2 – произвольные постоянные.
Запишем функцию (4.44) в более компактной форме. Для этого введем новые постоянные A и ϕ0 , а C1 и C2 будут связаны с A и ϕ0 соотношениями:
C1 = Asinϕ0 , C2 = Acosϕ0 . |
(4.45) |
Тогда постоянные A и ϕ0 через C1 и C2 определяются следующим обра- |
зом: |
|
|
|
= arctg C1 . |
|
A = C2 +C2 |
и ϕ |
0 |
|
1 |
2 |
|
C2 |
|
|
|
|
|
|
Подставляя значения C1 и C2 |
из (4.45) в уравнение (4.44), получим |
|
y = Asinϕ0 cosωt + Acosϕ0 sinωt |
|
или |
|
|
|
|
|
y = Asin (ωt +ϕ0 ). |
(4.46) |
Колебания, описываемые уравнением (4.46), называются гармоническими. Интегральными кривыми в этом случае являются синусоиды. График функции (4.46) изображен на рис. 4.5.
х
T = 2ωπ
Рис. 4.5. График функции (4.46)
Периодом колебаний называется промежуток времени Т, за который ар-
гумент синуса изменяется на 2π (в данном случае T = 2ωπ ).
Частотой колебаний называется число колебаний за время 2π (в нашем случае частота равна ω).
Амплитудой колебаний называется величина наибольшего отклонения от положения равновесия (в данном случае амплитудой является величина А).
Число ϕ0 называется начальной фазой.
II. Теперь рассмотрим решение ДУ (4.3) для случая, когда сила трения присутствует, т.е. μ ≠ 0 λ ≠ 0 . Характеристическое уравнение для (4.3)
имеет вид
p2 + 2λ p +ω2 = 0 . |
(4.47) |
Корнями уравнения (4.47) являются числа
p1,2 = −λ ± λ2 −ω2 = −λ ± λ ,
где λ < λ .
В зависимости от соотношения между λ и ω могут возникнуть три слу-
чая:
1. При λ =ω имеем p1 = p2 = −λ ( p1,2 < 0 ). Таким образом, применив формулу (4.41), запишем решение ДУ (4.3) в виде
y = e−λt (C +C |
t ). |
(4.48) |
1 |
2 |
|
|
Из уравнения (4.48) следует, что отклонение у при любых начальных условиях асимптотически стремится к нулю, если t →∞. В этом случае колебаний груза не будет, так как сила сопротивления велика по сравнению с коэффициентом упругости пружины k и в зависимости от начальных условий может наблюдаться один из видов апериодического движения (рис. 4.6).
2. При λ >ω имеем p1 = −λ + λ и p2 = −λ −λ ( p1,2 < 0 ). Значит, используя формулу (4.40), получим
y =C e(−λ+λ)t +C e(−λ−λ)t . |
(4.49) |
1 |
2 |
|
Здесь отклонение у также как и в первом случае будет асимптотически стремится к нулю при t → ∞, но, в отличие от предыдущего случая, гораздо быстрее.
143
у
а)
у
б)
t
в)
Рис. 4.6. Виды апериодического движения
3. При λ <ω имеем комплексные корни p = −λ ±i |
ω2 −λ2 = −λ ±ωi . |
|
|
1,2 |
|
Тогда, используя формулу (4.42), получим |
|
|
|
y = e−λt (C cosωt +C |
2 |
sinωt ) |
(4.50) |
1 |
|
|
или |
|
|
|
y = Ae−λt sin (ωt +ϕ0 ). |
(4.51) |
Здесь в качестве амплитуды нужно рассматривать величину Ae−λt , зави-
сящую от времени. Так как « −λ < 0 », то амплитуда Ae−λt будет стремиться к нулю при t → ∞, т.е. в этом случае мы имеем дело с затухающими колеба-
144
ниями, период которых равен T = |
2π |
~ |
|
|
2 |
2 |
|
(ω |
= |
ω |
|
−λ |
– частота затухающих ко- |
~ |
|
|
ω |
|
|
|
|
|
|
лебаний). График затухающих колебаний изображен на рис. 4.7.
у
Амплитуда
y = Ae−λt sin (ωt +ϕ0 )
Рис. 4.7. Затухающие колебания
5.КРИВИЗНА ПЛОСКОЙ КРИВОЙ
5.1.Определение кривизны
Одним из элементов, характеризующих форму кривой, является степень ее искривленности.
Пусть мы имеем кривую, которая не пересекает сама себя и имеет касательную в каждой точке. Проведем касательные к кривой в каких-нибудь двух ее точках А и В и обозначим через α угол, образованный этими касательными
(рис. 5.1).
 α
α
В
А
Рис. 5.1. Острый угол смежности
Углом смежности дуги AB называется угол α , на который поворачивается касательная при переходе от точки А к точке В.
У двух дуг, имеющих одинаковую длину, больше изогнута та дуга, у которой угол смежности α больше (рис. 5.1 и 5.2). Если длины двух кривых
не равны, то угол смежности α не может служить мерой кривизны. Поэто-
му для кривых разной длины вводят понятие средней кривизны.
Средней кривизной Kcp дуги AB называется отношение ее угла смежности α к длине дуги L , т.е.
 α
α
В
А
Рис. 5.2. Тупой угол смежности
В то же время, изогнутость разных частей дуги AB может быть различ-
ной. Поэтому вводят понятие кривизны линии в каждой точке.
Кривизной K линии в точке А называется предел средней кривизны дуги
AB , когда точка В приближается по дуге к точке А, при этом длина |
L этой |
дуги стремится к нулю |
|
|
|
|
|
|
|
|
|
|
K = lim Kcp = lim |
α |
. |
(5.2) |
|
B→A |
L→0 |
L |
|
|
Найдем кривизну прямой и окружности.
1. Касательная в каждой точке прямой совпадает с самой прямой. Поэтому α ≡ 0 , а следовательно, Kcp = K = 0 . Таким образом, прямая есть линия
нулевой кривизны.
2. Длина L дуги AB окружности (рис. 5.3) будет равна
L = AB = α R . 147
А
α
 α
α
R
 В
В
Рис. 5.3. Определение кривизны окружности
Таким образом, средняя кривизна Kcp у окружности
|
Kcp = α = |
α |
= |
1 |
|
= const , |
|
α R |
R |
|
L |
|
|
|
|
|
а кривизна К окружности в точке А |
|
|
|
|
|
|
|
|
|
K = lim Kcp = lim |
1 |
= |
1 |
. |
|
|
|
|
B→A |
B |
→A R |
|
R |
Следовательно, кривизна окружности в каждой точке есть величина постоянная и равная величине, обратной радиусу.
5.2. Вычисление кривизны графика функции
Рассмотрим график функции y = f (x), и некоторую произвольную точку M (x; y) на этом графике. Вычислим кривизну график функции в точке М. Предположим, что существует вторая производная f ′′(x) в точке х и в ее окре-
стности функция дифференцируема. Чтобы использовать определение кривизны линии в точке рассмотрим на кривой еще одну точку M1 с абсциссой
x + |
x . |
|
Проведем касательные к кривой в точках M и M1 с абсциссами x и |
x + |
x и обозначим через α и α + α углы наклона этих касательных к оси Ох |
|
148 |
(рис. 5.4).
Длину дуги M0M , отсчитываемую от некоторой фиксированной точки M0 , обозначим через L ; тогда L = M0M1 − M0M , а L = MM1 .
Из рис. 5.4 видно, что угол смежности, соответствующий дуге MM1 , равен абсолютной величине разности углов α и α + α , т.е. равен α .
y
y = f (x) |
M1 |
α |
|
M (x; y) |
|
|
M0 |
|
|
α |
α + α |
|
|
|
O |
x + x |
x |
x |
Рис. 5.4. Вывод формулы (5.4)
По определению средней кривизны дуги MM1 имеем
Чтобы вычислить кривизну в точке M (x; y), нужно найти предел полученного выражения при условии, что точка M1 стремиться по кривой к точке
М, т.е.
Очевидно, что из L →0 следует, что и x →0 , поэтому
|
|
α |
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
K = lim |
|
|
= lim |
|
x |
|
|
. |
(5.3) |
|
|
|
|
L |
|
L |
x→0 |
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
Из геометрического смысла производной имеем tgα = y′. Следовательно α = arctg y′, поэтому
lim |
|
α |
|
= |
|
dα |
|
= |
|
(arctg y′)′ |
|
= |
|
1 |
y′′ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
dx |
|
|
|
1+(y′)2 |
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кроме того,
lim L = dL = 1+(y′)2 ≠ 0 (см. формулу (3.31)). x→0 x dx
Таким образом, равенства (5.3) можно записать в виде
|
|
|
α |
|
|
|
lim |
|
|
α |
|
|
|
|
1 |
|
|
y′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
′ |
) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
x |
|
|
= |
x→0 |
|
|
|
|
= |
|
|
1+(y |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
1+(y′)2 |
|
|
|
x |
|
|
|
|
|
|
x→0 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И, окончательно, получим формулу для вычисления кривизны кривой |
y = f (x) в любой ее точке M |
(x; y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′′
K = 3 . (5.4)
1 +(y′)2 2
Таким образом, в любой точке кривой, где существует вторая производная y′′, можно вычислить кривизну.
Приведем здесь без вывода формулы кривизны кривой, заданной параметрически и в полярных координатах. Если линия задана параметрическими уравнениями x = x(t ) и y = y(t ), то







 α
α

 α
α В
В


 α
α