Математика. функции нескольких переменных, интегральное исчисление. практикум. Бырдин А.П., Сидоренко А.А

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Воронежский государственный технический университет»

А. П. Бырдин, А. А. Сидоренко, О. А. Соколова

МАТЕМАТИКА:

ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ, ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

Практикум

Воронеж 2021

УДК 517.9(075.8) ББК 22.161(я7)

Б95

Р е ц е н з е н т ы:

кафедра математического моделирования Воронежского государственного университета (зав. кафедрой д-р физ.-мат. наук, проф. В. А. Костин); И. В. Колесникова, канд. физ.-мат. наук, доцент кафедры математического анализа ВГУ

Изд-во ВГТУ, 2021. – 73 с.

ISBN 978-5-7731-0984-6

Практикум содержит теоретический материал, необходимый для решения прикладных задач, который иллюстрируется большим количеством примеров. Имеются задачи для самостоятельного решения и типовых расчетов.

Предназначен для студентов первого курса по направлению 18.03.01 «Химическая технология» (профиль «Технология неорганических и полимерных композиционных материалов»), дисциплине «Математика».

Ил. 14. Библиогр.: 6 назв.

УДК 517.9(075.8) ББК 22.161(я7)

Печатается по решению редакционно-издательского совета Воронежского государственного технического университета

4

ВВЕДЕНИЕ

При написании практикума авторы использовали опыт проведения практических занятий по курсу «Математика» для различных специальностей Воронежского государственного технического университета. В частности, данное издание предназначено для студентов очной формы обучения направления подготовки бакалавров «Технология неорганических и полимерных композиционных материалов» и написано в соответствии с рабочей программой этой специальности, но может быть использовано и для студентов других специальностей.

В практикуме представлен материал, который изучается во втором семестре. Цель работы – помочь студентам усвоить и закрепить основные положения функции нескольких переменных и интегрального исчисления.

При написании практикума авторы стремились изложить материал по возможности полно, строго и доступно. Представленная работа направлена на совершенствование учебного процесса и способствует целенаправленному использованию знаний математики. Практикум поможет студентам лучше усвоить теоретический материал, даст возможность самостоятельно научиться решать типовые задачи, подготовиться к экзамену или зачету.

По каждому разделу приведены примеры решения задач, а также многочисленные задачи для контроля усвоения материала. Ко всем рекомендуемым для самостоятельного решения задачам приведены ответы. Поэтому представленное издание полезно использовать преподавателями для проведения практических занятий.

Все приведенные в работе иллюстрации являются авторскими.

1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

1.1. Понятие функции двух переменных

Говорят, что определена функция z f (x, y) двух переменных x, y , если каждой паре значений независимых переменных (аргументов) x, y из области D

по некоторому закону f ставится в соответствие определенное значение переменной z из множества Z. Область D называется областью определения функции z, а множество Z- множеством значений функции. Поскольку каждой паре чисел x, y на плоскости Oxy можно поставить в соответствие точку

M (x, y) , то функцию двух переменных рассматривают как функцию точки М z f M из некоторой области D плоскости Oxy .

3

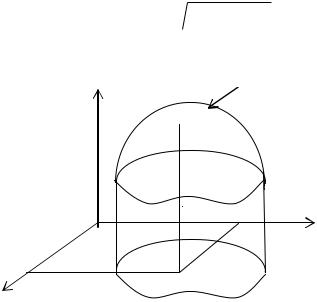
Геометрической интерпретацией функции двух переменных является поверхность (рис. 1), аппликата каждой точки которой вычисляется по закону

z f (x, y) . Например, для функции z 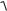1 x2 y2 геометрическим образом является верхняя полусфера. Область определения данной функции определяется неравенством 1 x2 y2 τ 0 или x2 y2 δ1.

Существует еще один способ изображения функции двух переменных, основанный на построении сечений поверхности z f (x, y) плоскостями z c ,

где с - любое число. Линией уровня называется множество точек плоскости Oxy , в которых функция принимает одно и то же значение с. Множество линий

уровня дает представление о поверхности подобно тому, как в картографии линии уровня описывают рельеф местности.

1.2. Частные производные и частные дифференциалы первого порядка

Пусть функция z f (x, y) определена и непрерывна в точке M0 (x0 , y0 ) и ее некоторой окрестности. Зафиксируем значение у = у0, а переменная х пусть

В определении частной производной по переменной x переменная у фиксирована, а х изменяется.

4

изменения функции z в точке M0 (x0 , y0 ) в направлении координатных осей Ox

и Oy .

При вычислении частных производных остаются в силе правила дифференцирования функции одной переменной, а также таблица производных, если другие аргументы считаются постоянными величинами.

Рассмотрим геометрический смысл частных производных функции двух переменных. Пусть уравнение z f (x, y) есть уравнение поверхности,

изображенной на рис. 2.

Проведем плоскость x x0 . В сечении этой плоскостью поверхности получается линия L2 . При данном х0 рассмотрим на плоскости точку М0. На

поверхности ей соответствует точка Р. Частная производная ωωyz равна тангенсу угла, образованного касательной к кривой L2 в точке М с положительным

5

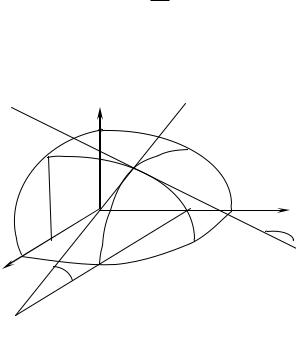
По аналогии частная производная ωωxz численно равна тангенсу угла наклона касательной к линии L1, представляющей сечение поверхности

Рис. 2

1.3. Полное приращение функции и полный дифференциал

бесконечно малой величиной более высокого порядка малости по сравнению сx и y , а частные производные функции являются непрерывными функциями

в некоторой окрестности точки M0 (x0 , y0 ) .

Линейная по x и y часть полного приращения функции f (x, y) называется полным дифференциалом функции f (x, y) в точке М0(х0,у0) и обозначается dz:

Если функция f (x, y) дифференцируема в точке M0 , то она непрерывна в этой точке.

6

Поэтому от них можно снова находить частные производные.

Частные производные от частных производных первого порядка называются частными производными второго порядка и обозначаются

второго порядка. Смешанные производные второго порядка, вычисленные с помощью различной последовательности дифференцирования по переменным

и т.д.

Рассмотрим дифференциалы второго и более высоких порядков для функции z f (x, y) , имеющей непрерывные частные производные высоких

порядков. Полный дифференциал первого порядка

содержит dx 'x и dy 'y. Эти величины не зависят от х и у, поэтому при

дифференцировании по х или у их можно считать постоянными.

Полный дифференциал от полного дифференциала первого порядка называется полным дифференциалом второго порядка и обозначается