Учебное пособие 1085

3)G – связный граф и m=n-1

4)G –связный граф, но при удалении любого ребра становиться несвязным

5)G – без циклов, но при добавлении любого ребра на тех же вершинах появляется цикл

Доказательство: Если доказать, что

1) 2) 3) 4) 5) 1), то из любого условия вытекает любое другое.

1) 2) Т.к. G – связный граф и G не содержит циклов, то n-m=1 по лемме 3. Отсюда m=n-1.

2) 3) По лемме 3 число связных компонент равно n- m=1, т.е. граф G – связный граф.

3) 4) При удалении одного ребра n-m=2. Тогда по лемме 3 число связных компонент не менее, чем n-m=2 т.е. граф несвязный.

4) 5) Если G имеет цикл, то согласно лемме 1 можно удалить одно ребро так, что граф останется связным. Согласно лемме 2, если добавить любое новое ребро к связному графу на тех же вершинах, то появиться цикл.

5) 1) Доказательство ведётся от противного. Предположим, что если G несвязный граф и вершины u и v лежат в разных компонентах графа G, но добавление к G ребра (u, v) очевидно, не порождает циклов, что противоречит 5). Отсюда следует, что G связный граф. Теорема доказана.

Вершина в графе называется концевой (висячей), если её степень равна 1. Ребро инцидентное концевой вершине называется концевым. Конечное дерево, состоящее более чем из одной вершины, имеет хотя бы две концевые вершины и одно концевое ребро.

Ориентированные, упорядоченные и бинарные деревья.

Ориентированным деревом (ордеревом, корневым деревом) называется орграф со следующими свойствами.

61

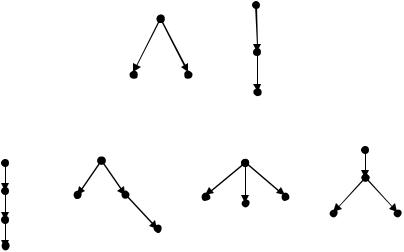
1)Существует единственная вершина, полустепень захода которой равна 0. Она называется корнем ориентированного дерева.

2)Полустепень захода всех остальных вершин

равна 1.

3)Каждая вершина достижима из корня.

Например:

а) все возможные ориентированные деревья с 3-я вершинами:

Рис. 22

б) с 4-я вершинами :

Рис. 23 Концевая (висячая) вершина ордерева называется лис-

том. Путь из корня в лист называется ветвью.

Уровень вершины ордерева – это расстояние от корня до вершины. Корень имеет уровень 0. Вершины одного уровня образуют ярус дерева.

Эквивалентное определение ориентированного де-

рева.

ОрдеревоD – это конечное множество вершин, таких

что:

62

1)имеется одна вершина r, называемая корнем данного дерева;

2)остальные вершины содержаться в k попарно непересекающихся множествах D1,…Dk , каждое из которых яв-

Множества D1,…,Dk называются поддеревьями. Упорядоченным деревом называется ориентированное

дерево, в котором:

1)задан порядок поддеревьев

2)каждое поддерево Di является упорядоченным поддеревом.

3)дерево с одной вершиной считается упорядоченным поддеревом.

Замечание. При изображении ориентированных деревьев принято соглашение о том, что корень размещается вверху. В связи с этим все дуги оказываются ориентированными сверху вниз, поэтому стрелки на них можно не изображать. В результате, диаграммы свободных, ориентированных и упорядоченных деревьев оказываются графически неотличимыми. В этом случае требуется дополнительное указание, какого класса дерево изображено на диаграмме. Обычно это ясно из контекста.

Например: Имеются 3 диаграммы деревьев:

Рис. 24

63

Как упорядоченные деревья, они все различны. Как ориентированные деревья D1=D2 D3. Как свободные деревья, они все изоморфны D1=D2=D3.

Терема 3. Число упорядоченных деревьев с mдугами не превосходит 4m.

Доказательство: Рассмотрим алгоритм обхода упорядоченного дерева, называемого «поиском в глубину». Этот обход рекурсивно описывается следующим образом:

1)Начать с корня. Пока есть деревья выполнять.

2)Перейти в корень очередного поддерева, обойти это поддерево в глубину.

3)Вернуться в корень исходного поддерева.

В результате «обхода в глубину» по каждой дуге проходят ровно 2 раза: один раз при переходе в очередное поддерево, второй раз – при возвращении из него. В соответствии с «обходом в глубину» строиться последовательность из нулей и единиц. На каждом шаге записывается нуль, если происходит переход в очередное поддерево, а единица – при возвращении из поддерева. В результате получается последовательность из нулей и единиц длины 2m, которая называется кодом дерева. По этому коду однозначно восстанавливается дерево, т.к. каждый очередной разряд однозначно указывает, начинать ли строить новое очередное поддерево или возвращаться на ярус ближе к корню. Таким образом, упорядоченных деревьев с m дугами не больше, чем последовательностей из нулей и единиц длины 2m. А их число равно 22m=4m. Теорема доказана.

Изоморфизм ориентированных деревьев определяется так же, как и изоморфизм графов, но с дополнительным условием - корень должен отображаться в корень. Для упорядоченных деревьев требуется также сохранение порядка поддеревьев.

Следствие. Число неизоморфных ориентированных или свободных деревьев с mребрами не превосходит 4m.

64

Доказательство: Выделив в неизоморфных свободных деревьях по одной вершине, мы получаем неизоморфные ориентированные деревья. Упорядочивая поддеревья в неизоморфных ориентированных поддеревьях, мы получаем упорядоченные деревья. Поэтому число неизоморфных свободных деревьев с m ребрами не превосходит числа неизоморфных ориентированных деревьев с m дугами, которое в свою очередь не превосходит числа неизоморфных (различных) упорядоченных деревьев с m дугами. Отсюда из теоремы 3 следует утверждение следствия.

Бинарное дерево – это конечное множество вершин, которое либо пусто, либо состоит из корня и не более двух непересекающихся бинарных поддеревьев – левого и правого. Заметим, что бинарное дерево не является упорядоченным.

Пример:На рисунке представлены два различных бинарных дерева:

Рис. 25 То есть, эти деревья изоморфны как упорядоченные, ориен-

тированные и свободные, но не изоморфны как бинарные деревья.

5.11. Эйлеровы графы.

Содержательная постановка задачи о Кенигсбергских мостах дана в теме 1. Переформулируем эту задачу в терминах теории графов. Для этого рассмотрим следующий неориентированный мультиграф/

65

Рис. 26

Вэтом графе вершины v1 и v4 соответствуют берегам,

аv2 и v3 – островам. Ребра отображают мосты. Таким образом, на языке теории графов исходная задача формулируется следующим образом: существует ли в указанном мультиграфе цикл, содержащий все ребра данного мультиграфа?

Определение: Цепь (цикл), содержащая все ребра графа и притом по одному разу, называется эйлеровой цепью (эйлеровым циклом). Граф, содержащий эйлеров цикл, называется эйлеровым графом.

Теорема. Для того, чтобы конечный связный неориентированный мультиграф был эйлеровым необходимо и достаточно, чтобы все его вершины имели чётные степени.

Доказательство:

Необходимость. Предположим, что граф является эйлеровым. Это значит, что, в нём есть эйлеров цикл. При этом каждый раз, когда эйлеров цикл проходит через какую-либо вершину, он должен войти в нее по одному ребру, а выйти по другому. Следовательно, условие отсутствия вершин нечетной степени является необходимым.

Достаточность. Предположим, что все вершины связного графаG имеют чётные степени. Тогда, в силу связности графа G, для всех его вершин выполняется условие d(v)>0.

Кроме того, в силу чётности вершин, должно быть d(v) 2для

66

n

всех v. По теореме Эйлера имеем:2m d(vi ) 2n .Это зна-

i 1

чит, что:m n или m n 1, и следовательно графG не является деревом, а поэтому он содержит хотя бы один простой цикл Z1 (Z1 - множество ребер), тогда G\Z1 – остовный подграф, в котором все степени вершин также четные. Исключим из рассмотрения изолированные вершины, тогда в графе G\Z1 существует простой цикл Z2 G\Z1, далее выделим Z3 и т.д. В результате этого получается разбиение множества ре-

ченного разбиения. Если Z1' E, то теорема доказана. Если нет, то в силу связности графа G, существуют цикл Z2' и

вершина v1 такие, что v1 Z1' и v1 Z2' . Маршрут, объеди-

няющий Z1' и Z2' , является циклом. Если Z1' Z2' E, то теорема доказана. Если нет, то имеется цикл Z3' , при котором существует вершина v2 такая, что v2 Z1' Z2' и v2 Z3' . Да-

лее будем наращивать эйлеров цикл до тех пор, пока не исчерпаем всё разбиение. В результате получаем эйлеров цикл всего графа.

Алгоритм построения эйлерова цикла в эйлеровом графе.

Этот алгоритм задается следующими правилами:

1)Выбирается произвольная вершина v.

2)Выбирается ребро e инцидентное вершине v и ему присваивается номер 1 (это ребро называется пройденным).

3)Каждое пройденное ребро вычеркивается и ему присваиваетсяномер на 1 больший номера предыдущего вычеркнутого ребра.

67

4)При нахождении в произвольной вершине x, не выбирается ребро, соединяющее x с v, если есть возможность другого выбора.

5)Ребро не проходится, если оно является перешейком. Перешейк – это ребро, при удалении которого, граф, образованный невычеркнутыми ребрами, распадается на две компоненты связности, каждая из которых имеет хотя бы одно ребро.

6)После того, как в графе будут занумерованы все ребра, образуется эйлеров цикл, нумерация рёбер которого соответствует последовательности обхода ребер.

Пример. Найти эйлеров цикл в эйлеровом графе

4

5

3

2

6

1

7

8 v

Рис. 27

После выбора вершины v и прохождения рёбер 1 и 2 имеется три возможности: выбрать 3,6 или 7. Ребро 7 является перешейком, поэтому выбирается любое из оставшихся рёбер, например 3. Далее идёт обход оставшихся рёбер получается эйлеров цикл.

68

5.12 Гамильтоновы графы.

Название «гамильтонов граф» произошло от задачи «кругосветное путешествие», придуманной Гамильтоном в 19 веке. Нужно обойти все вершины графа, изображенного на рисунке, по одному разу и вернуться в исходную точку.

Рис. 28 Гамильтоновой цепью неорграфа называется цепь,

проходящая через его вершину один и только один раз. Гамильтоновым циклом неорграфа называется цикл,

проходящий через каждую вершину один и только один раз, за исключением начальной вершины, совпадающей с конечной.

Граф, содержащий гамильтонов цикл называется гамильтоновым.

Гамильтоновым контуром называется контур орграфа, который проходит через все его вершины, причем только по одному разу.

Эйлеровы и гамильтоновы циклы сходны по способу задания. Эйлеровы содержат все ребра по одному разу, а гамильтоновы – все вершины так же по одному разу. Несмотря на это внешнее сходство, задачи отыскания соответствую-

69

щих циклов резко отличаются. Так для решения вопроса о существовании эйлерова цикла, достаточно выяснить четность всех вершин графа. Эффективного критерия существования гамильтонова цикла пока ещё не найдено. Известны лишь несколько теорем, дающих достаточные условия существования гамильтоновых циклов.

Теорема 1. В полном, конечном графе (любая пара вершин которого соединена хотя бы в одном направлении) всегда существует гамильтонов цикл.

Теорема 2. Если для любой пары несмежных вершин vi и vjграфа G сn вершинами справедливо неравенство d(vi)+d(vj) n , то граф обладает гамильтоновым циклом.

Теорема 3. Граф G с n вершинами имеет гамильтонов цикл, если для любой вершины vi выполняется неравенство d(vi) n\2,где n – число вершин в графе.

5.13. Планарные графы.

При изображении графа имеется полная свобода при размещении вершин и выборе формы соединяющих их ребер. Геометрическим графом называется множество точек в n-мерном евклидовом пространстве, взаимосвязанных между собой набором непрерывных самонепересекающихся кривых.

Теорема 1. В трехмерном пространстве любой конечный граф можно представить так, что линии, соответствующие ребрам (дугам) не пересекаются во внутренних точках.

Доказательство. Пусть граф G=(V,E) содержит n вершин и m рёбер. Возьмём прямую в трёхмерном пространстве и проведём через неё m различных плоскостей. На прямой выделим точки a1,a2, ,an , которые будут соответство-

70