Учебное пособие 254

входящих,

называется

частным

решением

это

дифференциального уравнения.

Определение 8.

Задача

о

нахождении

решения

уравнения (1), удовлетворяющего условиям

y(x0 ) = y0 , y ¢( x0 ) = y0¢,K, yn-1 ( x0 ) = y0n-1 ,

(2)

называется

задачей

Коши, условия (2)

-

начальными

Определение 9.

Дифференциальным

уравнением

первого порядка называется уравнение вида

¢

(3)

F (x, y, y ) = 0 ,

где х - независимая переменная, у - искомая функция, у′ — ее

производная.

можно разрешить относительно у′,

Если уравнение (3)

то оно принимает вид

y¢ = ( x, y)

(4)

y = j( x, C0 )

или F(x, y,C0 ) = 0 ,

где C0 определяется

из

начальных условий задачи Коши:

y( x0 ) = y0 .

решениеy = j( x,C )

Геометрически

общее

представляет собой

семейство

интегральных кривых на

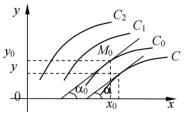
С, а частное решение y = j( x, C0 )

- одну интегральную

кривую этого семейства, проходящую

через заданную точку

(x0 , y0 ) (рис. 1).

Рис. 1

Таким

образом

геометрически

задача

Ко

формулируется

так: из

семейства

интегральных

кривых

уравнения (4) найти одну интегральную кривую, проходящую

через точку M0 (x0 , y0 ) .

Теорема

Коши (существования

и

единственности

решения задачи

Коши). Если функция f (x, y)

и

ее

частная

производная

¶f

определены

и

непрерывны

в

некоторой

¶y

области плоскости хОу

и, следовательно,

ограничены

в

ней,

то, какова бы ни была внутренняя точка (x0 , y0 )

этой области,

в некоторой окрестности этой точки существует единственное

решение задачи Коши:

y¢ = f ( x, y),ü

(x0 ) = y0 .

ý

þ

Определение 10.

Решение, в

каждой

точке

которого

нарушается

единственность

или

существование

решения

задачи

Коши,

называется

особым (геометрически:

совокупность точек плоскости, через которые либо проходит

более одной интегральной кривой, либо не проходит ни одной

Не

существует

общего

метода

интегрирования

дифференциального уравнения первого порядка. Обычно

рассматривают

лишь

некоторые

отдельные

типы

таких

уравнений, для каждого из которых дается

свой особый

способ решения.

X ( x)dx + Y ( y)dy = 0

(5)

называется уравнением с разделенными переменными.

Считая y = j( x)

известной,

это

уравнение

можно

рассматривать

как

сумму

двух

дифференциалов,

неопределенные

интегралы

от

них

будут

отличатьс

постоянным числом. То есть общий интеграл уравнения(5)

имеет вид

ò X ( x)dx + òY ( y)dy = C .

Определение 12. Уравнение вида

X1 (x)Y1 ( y)dx + X 2 (x)Y2 ( y)dy = 0

(6)

называется уравнением с разделяющимися переменными.

Уравнение

с

разделяющимися

переменными

может

X 2 (x)

Y1 ( y)

Определение 13.

Функция f (x, y)

называется

однородной

функцией п-го

измерения

относительно

переменных х и у, если при любом k справедливо тождество

f (kx, ky) = k n f (x, y) .

Определение 14.

Функция f (x, y)

называется

однородной

функцией

нулевого

измерения, если

при

умножении аргументов х и у

на

произвольный параметрk

значение функции не изменится:

f (kx, ky) = f (x, y) .

Определение 15.

Уравнением,

однородным

относительно переменных, называется уравнение вида

æ y ö

y¢ = f ç

÷ .

(7)

è

x ø

y

При решении однородного уравнения вводится замена

u =

, т.е.

y = ux ,

тогда

y¢ = ux + u .

Подставляя

это

x

для у′

выражение

в

однородное

уравнение, получим:

¢

или

¢

- u

-

это уравнение

с

u x + u = f (u)

u x = f (u)

разделяющимися переменными:

du

x = f (u) -u;

du

=

dx

.

f (u) -u

dx

x

Интегрируя, найдем:

ò

du

=

ò

dx

+ C .

f (u) - u

x

Замечание. Уравнение

M ( x, y)dy + N (x, y)dx = 0

(8)

будет

однородным

в

случае, если

M ( x, y), N (x, y) -

Линейные дифференциальные уравнения

Определение 16. Уравнение вида

y¢ + p(x) y = f ( x) ,

(9)

где p(x) и

f ( x)

-

непрерывные

функции, называется

линейным дифференциальным уравнением первого порядка.

Если

f (x) º 0 , то уравнение (9) называется линейным

однородным

уравнением.

Если f (x) ¹ 0 , то

уравнение (9)

называется

линейным

неоднородным

дифференциальным

уравнением.

Для нахождения общего решения уравнения(9) можно

пользоваться

следующим

способом. Будем

искать

решение

y(x) уравнения (9) в виде

y( x) = u(x) × v( x) ,

(10)

где u(x) и v(x) - неизвестные функции, одна из которых,

например v(x) , может быть выбрана произвольно.

Подставляя y(x)

в форме (10) в уравнение (9), учитывая, что

y

¢

¢

¢

= u ( x) × v(x) + u(x) × v ( x) , получим

u¢× v + u × v¢ + p( x) × u × v = g( x) .

После элементарных преобразований получим

u¢× v + u × (v ¢ + p(x) × v) = g(x) .

Выберем

в

качествеv(x) любое

частное

решение

v( x) ¹ 0 уравнения

v¢ + p(x) × v = 0 ,

тогда

u¢× v = g( x) .

Итак,

решение

уравнения (9)

сводится к

решению

Определение 17. Уравнение вида

y¢ + p(x) y = f ( x) yn ,

где p(x), f (x) - непрерывные

функции отх, а

n ¹ 0,

n ¹ 1 ,

называется уравнением Бернулли.

Это уравнение приводится к линейному следующим

образом

y-n y ¢ + p( x) y-n+1 = f (x) .

Вводится

замена z = y-n+1 .

Тогда

z¢ + (-n +1) y-n y ¢ ,

z ¢

+ p(x)z

= f (x) . Таким

образом,

получили линейное

-n +1

уравнение относительно функции z:

z¢ + (-n + 1) p(x)z = (-n +1) f (x) .

Получив его общий интеграл и подставив вместоz

выражение y-n +1 , получим

общий

интеграл

уравнения

Бернулли.

Замечание. Решение уравнения Бернулли можно искать

и в видеy = u( x) × v(x) , как

это

описано

при

решении

уравнения (9).

3. Дифференциальные уравнения второго порядка

Определение 18. Уравнение вида

¢

¢¢

F (x, y, y , y ) = 0

старшей производной,

y

¢¢

=

¢

(11)

f (x, y, y ) .

ì y ¢¢ = f (x, y, y ¢),

(12)

í

¢

¢

î y( x0 ) = y0 , y ( x0 )

= y0 .

Теорема

Коши (существования

и

единственности

задачи

Коши).

Если

функция

¢

¢

и

ее

частные

f (x, y, y )

производные

f y¢(x, y, y ¢)

и

f y¢¢ ( x, y, y¢)

определены

и

непрерывны

,и следовательно,

ограничены

в

некоторой

¢

области пространства переменных (x, y, y ) , тогда в любой

окрестности

точки (x0 , y0 , y0¢)

этой

области

существует

единственное

решение

¢¢

¢

уравненияy =

f (x, y, y ) ,

удовлетворяющее условиям y = y0 , y¢ = y0¢

при x = x0 .

Геометрически это означает, что через заданную точку

(x0 , y0 )

плоскости проходит

единственная

интегральная

кривая с заданным угловым коэффициентом y0¢

касательной в

точке (x0 , y0 ) .

Определение 19.

Функция y = j(x,C1 , C2 ) ,

зависящая

от х и

двух произвольных

постоянныхC

и C

2

и при

уравнение y

¢¢

¢

1

подстановке в

обращающая

его

в

= f (x, y, y )

тождество, называется общим решением этого уравнения.

Геометрически

общее

решение уравнения

второго

порядка

представляет

собой

бесконечную

совокупность