Учебное пособие 254

Правая часть

Корни

Вид частного решения

f ( x)

характеристи

y

ческого

уравнения

k 2

+ pk + q = 0

многочлен степени п с

неопределенными

коэффициентами

a cos b x,

k1,2

¹ ±bi

A cos b x + B sin b x

a sin b x,

k1,2

= ±bi

( Acos b x + B sin b x)x

a cos b x + b sin b x

А, В - неопределенные

коэффициенты

Pn (x) cos b x,

k1,2

¹ ±bi

Rn (x) cos b x +

Pn (x) sin b x,

+Sn (x) sin b x

Pn (x)(cos b x +

k1,2

= ±bi

x(Rn (x) cos b x +

+b sin b x)

+Sn ( x) sin b x)

Qn ( x) - многочлен

степени п с

неопределенными

коэффициентами

ea x

cos b x,

k1,2

¹ a ± bi

ea x ( A cos b x + B sin b x)

ea x

sin b x,

k1,2

= a ± bi

ea x x( A cos b x +

a x

(cos b x +

e

+B sin b x)

+b sin b x)

А, В - неопределенные

коэффициенты

Правая часть

Корни

Вид частного

f ( x)

характеристи

решения

y

ческого

уравнения

k 2

+ pk + q = 0

ea x P ( x) cos b x,

k1,2

¹ a ± bi

ea x (R ( x) cos b x +

n

n

ea x P ( x) sin b x,

+S

n

( x) sin b x)

n

ea x P ( x)(cos b x +

n

+b sin b x)

k1,2

= a ± bi

xea x (R ( x) cos b x +

n

+Sn ( x) sin b x)

Qn ( x) - многочлен

степени п с

неопределенными

коэффициентами

ea x (P ( x) cos b x +

k1,2

¹ a ± bi

ea x (R ( x) cos b x +

n

d

+Qm (x) sin b x)

+Sd ( x) sin b x)

k1,2

= a ± bi

xea x (R ( x) cos b x +

d

+Sd ( x) sin b x)

Rd ( x), Sd (x) -

многочлены степени

d = max(n, m) с

неопределенными

коэффициентами

y

¢¢

=

¢

(20)

f (x, y, y ) ,

решение которого удовлетворяет начальным условиям

y( x0 ) = y0 , y ¢(x0 ) = y0¢.

(21)

Решение данного

уравнения

найдем

в виде ряда

Тейлора:

¢

¢¢

y = y(x0 ) +

y ( x0 )

(x

- x0 ) +

y (x0 )

( x - x0 )2 + K

1!

2!

yn ( x )

K +

0

( x - x0 )n +K

n!

(22)

в котором первые два коэффициента сразу определяются из

начальных условий (21). Подставив в уравнение (20) значения

x = x0 , y = y0 ,

y¢ = y0¢ ,

находим

третий

коэффициент

y¢¢( x0 ) = f (x0 ; y0 ; y0¢¢) .

Путем

последовательного

дифференцирования

уравнения (20)

и

вычисления

производных

при x = x0

найдем значения y¢¢¢(x0 ), y(4) (x0 ) .

Найденные

значения

производных(коэффициентов)

y¢¢ + p(x) y ¢ + q( x) y = f ( x) ,

(23)

с

начальными

условиямиx = x0 , y = y0 , y ¢ = y0¢ .

Искомое

y = a0

+ a1 (x - x0 ) + K + an ( x - x0 )n + K ,

(24)

предполагая,

что функции p(x), q(x) и f (x)

разлагаются в

коэффициенты

разложения (24)

находим, дифференцируя

равенство (24)

два раза (каков

порядок уравнения), и

Вид уравнения

Способ решения

Дифференциальные уравнения первого порядка

Уравнения с

разделяющимися

переменными:

1. X1 (x)Y1 ( y)dx +

1.1. X1 (x)Y1 ( y)dx = X 2 (x)Y2 ( y)dy

+X 2 (x)Y2 ( y)dy = 0

1.2.

X1 (x)

dx +

Y2 ( y)

dy

X 2 (x)

Y1 ( y)

dy

2. y¢ = f1 ( x) × f2 ( y)

2.1.

= f1

(x) × f2 ( y)

dx

2.2.

dy

= f1 (x)dx

f2 ( y)

2.3.

ò

dy

=

ò

f1 ( x)dx + C

f2 ( y)

Однородное

1.

Вводится замена u =

y

, т.е. y = ux .

уравнение

x

æ y ö

2.

Получаем y

¢

¢

y¢ = f ç

÷

= u x + u .

3.

Подставляем в однородное

è

x ø

уравнение:

¢

= f (u) - u .

u x

4.

du

=

dx

.

f (u) - u

x

5.

Интегрируя, найдем:

ò

du

= ò

dx

+ C

f (u) - u

x

Линейное

1.

Введем замену:

y( x) = u(x) × v( x) ,

уравнение

тогда y

¢

¢

¢

y¢ + p(x) y = f ( x)

= u ( x) × v(x) + u(x) × v ( x) .

2.

Получаем

u¢× v + u × (v ¢ + p(x) × v) = g(x)

1. y

¢¢

= f (x) не

1.1. Вводим замену y

¢

= p(x), y

¢¢

¢

= p (x) .

содержит явно у и

1.2. y¢ = ò f ( x)dx + C1 .

у′

é

ù

+ C1 x + C2

1.3. y = ò ëò f ( x)dx

ûdx

2. y

¢¢

=

¢

2.1. Полагая y

¢

= p(x), y

¢¢

¢

f (x, y ) не

= p (x) , т.е.

содержит явно у

p¢ = f (x, p)

3. y

¢¢

¢

y = òj(x,C1 )dx + C2

3.1. Полагая y¢ = p( y(x)) . Тогда

= f ( y, y ) не

содержит явно х

y¢¢ = p¢× p .

3.2. Подставляя в уравнение, получим

p × p¢ = f ( y, p) .

3.3. Решая его, найдем p =j( x, C1 ) ,

отсюда

dy

= dx .

j( y, C1 )

3.4. ò

dy

= x + C2

j( x, C )

1

Линейное

Составляем характеристическое

однородное

уравнение: k 2

+ pk + q = 0 .

уравнение

Если k

¹ k

, то y = C ek1 x + C ek2 x .

y¢¢ + py¢ + qy = 0

1

2

1

2

Если k

= k

2

, то y = C ek1 x + C

2

xek1x .

1

1

Если k1,2 = a ± bi , то

y = eax (C cos b x + C sin b x)

1

2

Линейное

1. Решаем соответствующее

неоднородное

однородное уравнение y¢¢ + py¢ + qy = 0 .

уравнение

2. По виду правой части уравнения

y¢¢ + py¢ + qy = f ( x) ,

записывается

форма частного решения

f ( x) имеет

с неопределенными коэффициентами.

специальный вид

3. Таким

образом

сформированное

в

частное

решение

подставляется

дифференциальное уравнение.

определяются

зн

коэффициентов.

5. y = y0 +

y

cos2 y ctg xdx + sin2

x tg ydy = 0 .

Решение. Разделим переменные в данном уравнении,

поделив обе части на выражение cos2

y sin2 x :

-

ctg xdx

=

tg ydy

.

sin2

x

cos2

y

Интегрируя обе части данного равенства, получим

-ò

ctg xdx

=

ò

tg ydy

,

sin

2

x

cos

2

y

откуда

ctg2

x

+ C =

tg2

y

.

2

2

Решение.

Разрешим

уравнение

относительно

производной

dy

: y¢ =

x2 + y2

.

dx

xy

Поделив

числитель

и

знаменатель

правой

части

уравнения на x2 , получим:

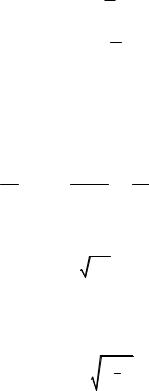
æ y ö2

1 + ç

÷

y¢ =

è

x ø

,

y

u =

y

. Тогда

y = ux и y¢ =

du

x + u . Тогда уравнение

x

dx

dx

u

x

ln

x

+ ln

C

=

u2

Интегрируя

это уравнение, получим

,

2

откуда ln

x × C

=

u2

, Þ xC =

eu2 .

равенствеu

y

2

Заменяя

в

последнем

отношением

,

окончательно получим

x

æ y ö2

xC =

ç

÷

eè x ø .

Пример 3. Найти общее решение линейного уравнения

y¢ - y tg x = sin x .

Решение.

Положим

y = u

× v , тогда

y

¢

¢

+ uv

¢

и

= u v

данное уравнение примет вид

¢

¢

¢

¢

- v tg x)

= sin x .

u v + uv

- uv tg x = sin x Þ u v + u(v

Решая

уравнение v¢ - v tg x = 0 ,

получим

простейшее

частное решение:

dv

= v tg x;

dv

= tg xdx; ln

v

= -ln

cos x

; v =

1

.

dx

v

cos x

Подставляя

v

в

¢

1

уравнениеu v = sin x , получим

u¢

= sin x , из которого находим u:

cos x

du

1

= sin x; du = sin x cos xdx;

dx cos x

u =

sin2

x

+ C.

2

Итак, искомое общее решение примет вид

æ sin2

x

ö

1

.

y = uv = ç

+ C ÷

2

Пример 4.

è

ø cos x

Найти

общее

решение

уравнен

y¢¢ + 6 y ¢ + 9 y =14e-3x .

Решение. Общее решение

уравнения

ищем в

виде

y = y0

+

y

:

k 2 + 6k + 9 = 0 Þ k = k

2

= -3 .

1

Следовательно, по теореме 7

y = (C + C

2

x)e-3x .

0

1

2) Найдем теперь

y

.

Здесь

правая часть имеет вид

f (x) = ekx P ( x) , где k = -3, P (x) = A . Так как k = -3 является

n

n

двукратным корнем

характеристического уравнения, т.е.

члены,

в

итоге

получим2 A =14 ,

откуда

A = 7 .

Следовательно,

искомое

частное

решение

имеет

вид

y

= 7x2 e-3x .

Итак, общее решение данного уравнения –

y = y

0

+

y

= (C + C

2

) xe-3 x + 7x2 e-3 x .

1

Пример 5. Найти общее решение уравнения

y¢¢ - 4 y¢ + 3y = x + 2 .

Решение: Общее решение соответствующего однородного

уравнения имеет вид

= C e x

e3x .

y

оо

+ C

2

1

Так как правая часть данного неоднородного уравнения имеет вид

(x + 2)e0 x , где параметр правой части a + ib =0 и не совпадает с

корнями характеристического уравнения k1 = 1 и k2 = 3 , то

частное решение ищется в виде y

чн

= Q (x)e0 x

= Ax + B .

1

Подставляя это выражение в заданное уравнение, имеем

- 4 A + 3( Ax + B) = x + 2 .

Приравнивая коэффициенты при одинаковых степенях х,

получим

3A = 1, - 4A + 3B = 2 ,

откуда

A = 1/ 3,

B = 10 / 9. Следовательно,

yчн =

1

x +

10

.

3

9

Общее решение дифференциального уравнения равно

y = C e x + C

2

e3x +

1

x +

10

.

1

3

9

Пример 6. Найти общее решение дифференциального

уравнения

y¢¢ - 5y¢ + 4 y = (x - 2)e x .

Решение: Общее решение соответствующего однородного

уравнения имеет вид

= C e x

e4 x .

y

оо

+ C

2

1